|
|
Фазовый метод измерения толщины неферромагнитных электропроводящих покрытий на неферромагнитном электропроводящем основании
Как упоминалось ранее, измерение толщины электропроводящего покрытия – это измерение значения интегральной электропроводности в объеме металла, в котором распространяются вихревые токи. На рис. 2.58, а) изображен годограф вектора разностного напряжения ∆Ů при изменении обобщенного параметра b (электропроводности полупространства). Выбор оптимальных параметров преобразователя, в первую очередь, диаметра и частоты возбуждения, должен производиться с использованием этим данных. На рис. 2.58, б) изображен график зависимости проекции приращения вектора разностного напряжения ∆Ů при изменении электропроводности полупространства на нормаль к направлению влияния зазора от начального значения обобщенного параметра b.
а)
Рис. 2.58. График зависимости разностного напряжения от обобщенного параметра b: а - годограф вектора разностного напряжения ∆Ů при изменении обобщенного параметра b (электропроводности полупространства, при h*=0,5), б - график зависимости проекции приращения вектора разностного напряжения ∆Ů при изменении электропроводности полупространства на нормаль к направлению влияния зазора от начального значения обобщенного параметра b
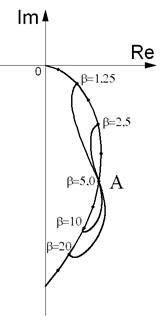
Из рис. 2.58, б видно, что при начальном значении b = 5, увеличение или уменьшение его приводит к наибольшему изменению фазы вектора разностного напряжения ∆Ů в случае измерения толщины с отстройкой от влияния зазора. Для расчета значения b следует использовать значение электропроводности основания, а не покрытия. Таким образом, при решении задачи измерения толщины этой группы покрытие/основание, исходя из электропроводности основания, можно рассчитать оптимальное соотношение частоты преобразователя и его диаметра. Это соотношение определяется по формуле: __ ___ RÖw = (Ös0 m0)/ 5 , (2.12.1) где R – эквивалентный радиус преобразователя. Частота возбуждения и радиус преобразователя выбираются исходя из максимальной толщины покрытия и технологических ограничений на диаметр и частоту возбуждения. Изменение толщины электропроводящего покрытия приводит к изменению фазы вектора разностного напряжения ∆Ů по нелинейному закону, и в некоторых случаях даже не по монотонному. Это связано с тем, что вихревой ток различной плотности в покрытии и в основании влияют друг на друга, искажая общую картину вторичного магнитного поля. Поэтому говорить о неком интегральном значении электропроводности можно только условно. Для уточнения влияния изменения толщины покрытия на показания толщиномера, на рис. 2.59 изображены годографы изменения вектора разностного напряжения ∆Ů при изменении толщины покрытия различной электропроводности. Параметры преобразователя выбраны оптимальными, при которых b(sосн) = 5 (точка А).
Рис. 2.59. Годографы изменения вектора разностного напряжения ∆Ů при изменении толщины покрытия различной электропроводности.
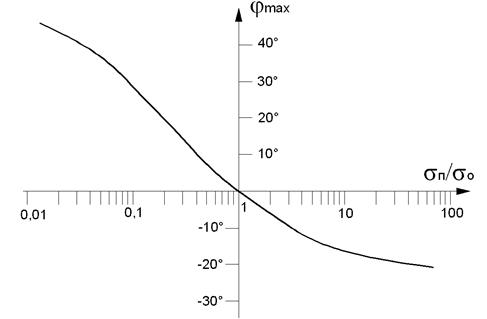
В случае, если sП < sосн конец вектора ∆Ů будет располагаться выше точки А, если sП > sосн конец вектора ∆Ů будет располагаться ниже точки А. График зависимости максимального изменения фазы вектора напряжения ∆Ů при изменении толщины покрытия от 0 до 2pd от отношениях электропроводностей покрытия и основания sП / sосн приведен на рис. 2.60.
Рис. 2.60. Зависимость максимального изменения фазы вектора ∆Ů при изменении толщины покрытия от 0 до 2pd от отношения sП / sосн.
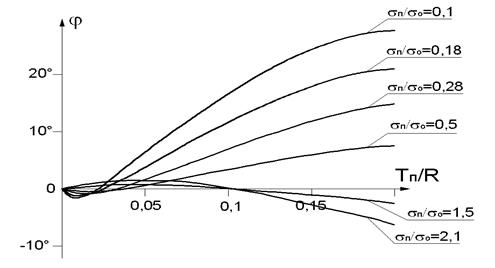
График зависимости фазы вектора напряжения ∆Ů от относительной толщины покрытия ТП/R приведен на рис. 2.61.
Рис.2.61. График зависимости фазы вектора напряжения ∆Ů от относительной толщины покрытия ТП/R.
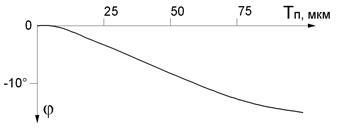
Из рис. 2.61 видно, что в определенном диапазоне малых толщин покрытий возникает неоднозначность. Фаза вектора напряжения ∆Ů вначале имеет один знак, затем пересекает ось начального значения, а затем изменяется в противоположную сторону вплоть до насыщения. Этот небольшой участок неопределенности называется «мертвой зоной» вихретокового фазового толщиномера. Поэтому вихретоковые фазовые толщиномеры не могут измерять толщину покрытий данной группы от нуля, всегда существует некоторое значение минимальной измеряемой толщины покрытия. Изменяя балансировку и параметры преобразователя можно уменьшить величину «мертвой зоны», однако полностью от неё избавиться невозможно. Рассмотрим пример измерения толщины серебряного покрытия на латунном основании. Электропроводность латуни Л63 sосн = 9,3 МСм/м, электропроводность серебра sП = 60 МСм/м. Отношение sП / sосн » 6,5. Исходя из графика на рис. 2.61 максимальное изменение фазы вектора ∆Ů » 15°. Конструктивный заданный радиус преобразователя R =1,3 мм. Расчетное значение оптимальной частоты f » 200 кГц. На рис. 2.62, а изображен годограф изменения вектора ∆Ů при изменении толщины, на рис. 2.62, б изображен график зависимости изменения фазы вектора ∆Ů от толщины покрытия (градуировочная характеристика).
а) Рис. 2.62. Изменение вектора напряжения ∆Ů при изменении толщины серебряного покрытия на латунном основании: а – годограф, б - график изменения фазы (градуировочная характеристика)
Из (2.1.9) следует, что максимальная глубина проникновения вихревого тока d » 200 мкм. Иногда в качестве подслоя под серебро используют слой медного покрытия. Учитывая, что электропроводность чистой меди практически не отличается от электропроводности серебра, при измерении толщины такого двухслойного покрытия результатом будет суммарная толщина медного и серебряного покрытий. Измерение толщины неферромагнитных электропроводящих покрытий на неферромагнитном электропроводящем основании с применением фазового метода возможно при достаточном отличии электропроводностей покрытия и основания, в противном случае фазовые сдвиги не позволят получить приемлемой погрешности измерений. |
|
 б)
б) 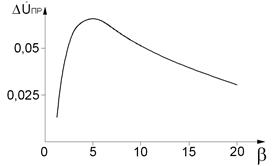
 б)
б)