|
|
Распределение заряда, концентрации подвижных носителей, поляи потенциала в p-n переходе 5.3.1. Ступенчатый р-n переход
Рассмотрим решение для x > 0 (рисунок 5.6),
При x > 0, Тогда Концентрация электронов в ОПЗ
В большинстве случаев контактная разность потенциалов составляет более полуширины запрещенной зоны, т.е. десятые доли электронвольта. Поэтому для всей практически толщины ОПЗ в n-области, где выполняется условие
Поэтому
Рисунок 5.6 - P-n переход (а), распределение заряда (б), концентрации подвижных носителей в линейном масштабе (в), логарифмическом (г), поля (д), потенциальной энергии и потенциала (е)
После первого интегрирования (5.5) получим:
, откуда следует: .
Выражение для напряженности поля:
В ОПЗ n-области поле линейно падает от
Второе интегрирование (5.8) позволяет определить зависимость потенциала от координаты
Потенциал по координате (потенциальная энергия электронов Ф(х)) изменяется по параболическому закону. Аналогично решаем (5.5) для р-области, x < 0. В этом случае объемный заряд
После первого интегрирования (5.5) получим:
Из условия непрерывности напряженности поля в однородной среде
Глубина проникновения контактного поля обратно пропорционально уровню легирования полупроводника. Для несимметричного p+-n перехода (Na >> Nd),
<< ; .
Все контактное поле локализовано в слаболегированной n-области.
В силу непрерывности потенциала:
Из этого выражения следует:
. Ширина области пространственного заряда.
Подставив эти выражения в (5.12) для модуля U0, получим:
Откуда следует: Толщина ОПЗ определяется контактной разностью потенциалов и уровнем легирования полупроводника. Чем сильней легированы p-и n-области, тем меньше ширина ОПЗ. Если ввести обозначение:
Для несимметричного резкого p+-n перехода (Na >> Nd),
δ совпадает с толщиной барьера Шоттки запорного контакта металл-полупроводник ( 5.3.2. Плавный p-n переход Плавный p-n переход реализуется методами диффузии, вытягивания из расплава, управляемой эпитаксии. Зачастую ОПЗ занимает малую часть общего распределения примесей по координате. Это приближение дает возможность решить уравнение Пуассона в явном виде:
Для линейного р-п перехода значение концентрации (рисунок 5.7, б) Поэтому
Используется треугольная аппроксимация объемного заряда (рисунок 5.7, в).
Напряженность контактного поля
В плавном (линейном) p-n переходе напряженность контактного поля распределяется по параболе (рисунок 5.7, д). Интегрирование (5.19) с учетом первого равенства граничных условий (5.18) приводит к следующему выражению:
Рисунок 5.7 - P-n переход (а), распределение примесей (б), объемного заряда (в), концентрации носителей (г), поля (д), потенциального барьера и потенциала (е)
Используя первое равенство в (5.17), получим:
(5.23)
Контактную разность потенциалов линейного p-n перехода можно рассчитать из трансцендентного уравнения:
Величина контактной разности потенциала определяется градиентом концентрации примесей и находится в диапазоне: Линейный переход более высоковольтный, чем ступенчатый. При одинаковом обратном напряжении максимальная напряженность плавного перехода меньше, чем у ступенчатого. Условие ударной ионизации или лавинного пробоя в плавном переходе наступает при большем обратном напряжении (площадь, ограниченная кривой 5.4. P-n переход в неравновесных условиях Прямое смещение
Величина результирующего барьера:
Толщина барьера (5.13 а):
Рисунок 5.8 - P-n переход в прямом смещении (а); распределение поля (б); потенциальной энергии (в)
Понижение потенциального барьера приводит к нарушению равновесия токов. Диффузионные потоки электронов и дырок возрастают, а дрейфовые уменьшаются. В результате будет протекать ток в направлении от плюса к минусу:
Одновременно увеличивается концентрация подвижных носителей заряда обоих знаков в ОПЗ, что ведет к уменьшению сопротивления p-n перехода с ростом прямого тока. Энергетическая диаграмма p-n перехода в прямом смещении приведена на рисунке 5.9. Увеличение концентрации неосновных носителей заряда, дырок в n-области, электронов в р-области называется инжекцией.
Рисунок 5.9 - Энергетическая диаграмма p-n перехода в прямом смещении
За время релаксации Максвелла (практически мгновенно) этот заряд неосновных носителей нейтрализуется основными, которые поступают из источника: В случае малых уровней инжекции
Неравновесная концентрация неосновных носителей (5.2)
Выражение (5.26) представляет собой граничные условия Шокли. Концентрация неосновных носителей заряда (ННЗ) в p-n переходе изменяется экспоненциально с величиной приложенного смещения. Избыточная концентрация ННЗ приводит к возникновению градиента концентрации и диффузионных токов в базах p-n перехода на расстоянии порядка трех диффузионных длин. По мере диффузии неосновных носителей происходит рекомбинация с основными и замыкание тока на источник (см. раздел 3.7). За тремя диффузионными длинами диффузионные токи исчезают, и непрерывность тока обеспечивается дрейфовыми токами основных носителей заряда. Для отражения избыточной концентрации на энергетической диаграмме вводят квазиуровни Ферми. Квазиуровни Ферми позволяют оценить неравновесную концентрацию с помощью равновесной функции распределения Ферми-Дирака, либо Больцмана для невырожденных полупроводников. Для прямого смещения концентрация носителей в p-n переходе со стороны р-области:
Эта же концентрация описывается квазиуровнями Ферми
Сделав произведение правых и левых частей этих равенств, получим:
Следовательно, приложенное смещение определяет разность квазиуровней Ферми на малых уровнях инжекции
По мере удаления от p-n перехода концентрация ННЗ уменьшается за счет рекомбинации, соответственно квазиуровень Fn удаляется от Ec в p-области, а квазиуровень Fp от Ev в n-области. На трех диффузионных длинах квазиуровни совпадают с равновесными уровнями Ферми (нет избыточных носителей). Концентрацию основных носителей описывают равновесные уровни Ферми (очень мала добавка ОНЗ). На больших уровнях инжекции вводят квазиуровни Ферми и для ОНЗ. Избыточная концентрация ННЗ определяется разностью равновесной и неравновесной концентрацией носителей (рисунок 5.10, а).
Рисунок 5.10 - Распределение концентрации носителей (а) и токов (б) в прямосмещенном p-n переходе
Так как произведения равновесных концентраций в p-базе и n-базе одинаковы,
то в логарифмическом масштабе
сумма ординат n и p в обоих базах должно быть равной На удалении трёх диффузионных длин от р-n перехода ток поддерживается дрейфом основных носителей. Это означает, что полной нейтральности базы не существует. Так как концентрация основных носителей велика ((1015 – 1018) см-3), то для поддержания тока требуется малая напряженность поля, при которой полевые токи ННЗ практически равны нулю (из–за малой концентрации ННЗ). Следовательно, понятие нейтральности базы относится только к ННЗ. В прямом смещении концентрация ННЗ возрастает по экспоненте с напряжением. В общем случае плотность тока можно представить произведением заряда на поток носителей:
где Следовательно, ток p-n перехода в прямом смещении будет сверхлинейно возрастать (по экспоненте) с напряжением, а сопротивление p-n перехода падать обратно пропорционально току. В прямом смещении через p-n переход протекает ток.
Обратное смещение
При обратном смещении величина результирующего барьера (рисунок 5.11, в) возрастает,
Рисунок 5.11 - P-n переход в обратном смещении (а), распределение поля и потенциального барьера (в)
Толщина барьера увеличивается (5.11а)
Повышение барьера при обратном смещении приведёт к ограничению надбарьерных диффузионных потоков: электронов из n-области в p-область и дырок из p-области в n-область. Равновесие токов сдвигается в сторону полевых компонентов (рисунок 5.11, а)
Направление потока электронов противоположно направлению плотности тока как диффузионного, так и полевого. Оценим концентрацию ННЗ на границах ОПЗ с квазинейтральными областями (5.2),
Поле обратно смещённого р-n перехода полностью экстрагирует концентрацию ННЗ. В стационарных условиях эти градиенты концентрации поддерживаются тепловой генерацией. Величина этих диффузионных токов в точности соответствуют дрейфовым компонентам в ОПЗ. Генерация за тремя диффузионными длинами не даёт вклада в обратный ток, так как носители не могут долететь до границы ОПЗ и захватиться полем (они рекомбинируют).
Рисунок 5.12 - Распределение концентрации носителей заряда в р-n переходе при обратном смещении
Распределение токов в р-n переходе при обратном смещении аналогично прямому смещению (рисунок 5.10, б). Отличие только в том, что в прямом смещении в ОПЗ механизм переноса тока диффузионный, а в обратном смещении – полевой. Величина плотности токов в прямом смещении на порядки превышает плотность тока при обратном смещении, так как концентрация основных носителей заряда, обеспечивающих инжекцию при прямом смещении на много порядков превышает концентрацию неосновных носителей, экстракция которых формирует обратный ток р-n перехода. Таким образом, природа обратного тока обусловлена тепловой генерацией ННЗ в квазинейтральных базах, экстракцией ННЗ полем обратно смещённого p-n перехода, диффузией ННЗ из баз к ОПЗ, дрейфом дошедших до границ ОПЗ неосновных носителей в поле ОПЗ, и переходом этих носителей в другую базу, где они становятся основными и замыкаются на источник питания. Кроме тепловой генерации в квазинейтральном объёме баз p-n перехода существуют и другие компоненты обратного тока, обусловленные генерацией в объёме и на поверхности ОПЗ, на квзинейтральной поверхности, омическом контакте, канальных областях. Эти компоненты обратного тока будут в дальнейшем рассмотрены. Энергетическая диаграмма p-n перехода в обратном смещении приведена на рисунке 5.13. Квазиуровни Ферми отражают неравновесную концентрацию ННЗ. Например, концентрация электронов в p-базе определяется энергетическим зазором Таким образом, качественное рассмотрение процессов в р-n переходе в неравновесных условиях внешнего смещения приводит к выводу, что вольтамперная характеристика p-n перехода должна иметь нелинейный характер и обладать выпрямительными свойствами (рисунок 5.14). В прямом смещении р-n переход пропускает ток (малое сопротивление), в обратном смещении p-n переход не пропускает ток (мал обратный ток, большое обратное сопротивление).
Рисунок 5.13 - Энергетическая диаграмма p-n Рисунок 5.14 - Вольтамперная характеристика перехода при обратном смещении p-n перехода
Для получения количественной связи между током и напряжением и их зависимостями от физических параметров р-n перехода, необходимо в общем случае определить распределение концентрации подвижных носителей зарядов, на основе которых можно оценить диффузионные и дрейфовые токи. С этой целью используются фундаментальные уравнения физики полупроводников (3.66 – 3.69), и в первую очередь уравнения непрерывности и уравнение Пуассона. Зачастую задачи не имеют аналитического решения в явном виде и успех моделирования зависит от правильной постановки краевых и граничных условий. Диодная теория выпрямления на p-n переходе, является ярким примером, подтверждающим особую значимость правильно выбранных физических допущений и граничных условий, позволивших сравнительно простыми математическими средствами получить вольтамперную характеристику р-n перехода. Основные допущения: 1. Толщина ОПЗ значительно меньше диффузионных длин 2. Квазинетральность базы для неосновных носителей заряда. Дрейфовые токи ННЗ отсутствуют. Справедливо для малых уровней инжекции. 3. Базы полубесконечны 4. В обратном смещении отсутствуют эффекты сильных полей. Обратное напряжение ниже напряжения пробоя. 5. Одномерный случай. Плоский р-n переход. Толщина структуры меньше поперечного (латерального) размера. Граничные условия: 1. Концентрация неосновных носителей заряда в неравновесном состоянии подчиняется граничным условиям Шокли (5.26)
2. Концентрации избыточных неосновных носителей заряда на + ¥ и – ¥ равны нулю.
3. Суммарный ток через p-n переход можно представить суммой диффузионных токов ННЗ на границах ОПЗ с квазинейтральными базами. Следствие допущения 1:
Именно это граничное условие позволяет отказаться от одновременного решения уравнения Пуассона, существенно усложняющего математическую задачу. Для определения распределения концентрации неосновных носителей зарядов в базах p-n перехода воспользуемся уравнением непрерывности. При где В одномерном приближении: Учитывая допущение 2 (
где Обозначим
решение которого представляет собой суперпозицию двух экспонент:
Переходя к концентрации дырок, запишем:
Воспользуемся граничным условием 2, Откуда следует
Постоянная интегрирования A:
Подставив это значение в (5.29), получим:
(5.30 а)
Аналогично для электронов в p-базе:
(5.30 б)
Избыточная концентрация неосновных носителей заряда и их диффузионные токи убывают за счёт рекомбинации по мере удаления от границ ОПЗ по экспоненциальному закону с характеристическим расстоянием – диффузионная длинна (рисунок 5.15). Нетрудно показать, что касательные к кривым
Рисунок 5.15 - Распределение избыточной концентрации неосновных носителей заряда на границах ОПЗ
Зная распределение n(x), p(x), можно записать выражение для плотностей тока на границах ОПЗ:
Ток через p-n переход (граничное условие 3) определяется суммой диффузионных токов на границе ОПЗ:
где
Выражение (5.32) отражает выпрямительные свойства p-n перехода. В прямом смещении ток экспоненциально растет с приложенным смещением, а дифференциальное сопротивление перехода уменьшается с ростом тока
В обратном смещении при Ток меняет направление и определяется диффузионным током неосновных носителей заряда, и не зависит от напряжения (рисунок 5.14). Дифференциальное сопротивление стремится к бесконечности,
Связь тока насыщения с физическими параметрами p-n перехода
Для отражения зависимости jS0 от уровня легирования воспользуемся соотношением
тогда
Плотность тока насыщения обратно пропорциональна уровню легирования (ND , NA) баз p-n перехода и экспоненциально уменьшается с ростом ширины запрещенной зоны полупроводника Воспользовавшись соотношением для диффузионной длины:
получим:
 , ,
а) б) в) Рисунок 5.16 - Зависимость jS0 от уровня легирования (а); ширины запрещенной зоны (б) и времени жизни ННЗ (в) Несимметричный резкий p-n переход В ряде случаев необходимо обеспечить ток преимущественно одного типа носителей заряда, например, в эмиттере биполярного транзистора. C этой целью эмиттер выполняется в виде несимметричного p+-n или n+-p перехода. Для p+-n перехода:
Плотность тока насыщения
и прямой ток определяются дырками (рисунок 5.17).
Рисунок 5.17 - Распределение тока в несимметричном резком p+-n переходе
В несимметричном p+-n переходе все контактное поле локализовано в слаболегированной n-базе d ≈ Ln, как и в случае запорного контакта металл – полупроводник. Для отражения состава тока в p+-n переходе вводят понятие коэффициент инжекции, который определяет долю, инжектированного в слабо легированную базу тока, в полном токе,
Воспользовавшись (5.33), получим:
При Na/Nd > 103, дробь (5.35) можно разложить в ряд Тейлора и ограничиться первым членом.
Значение коэффициента инжекции 0,99 означает, что протекающий ток обеспечивается на 99% дырками и лишь только сотая часть тока обусловлена обратной инжекцией из слаболегированной области в сильнолегированную.
|
|

 . (5.5)
. (5.5) . (5.6)
. (5.6) ,
,  .
. .
. .
. , концентрацией электронов можно пренебречь
, концентрацией электронов можно пренебречь . (5.7)
. (5.7) – прямоугольная аппроксимация объемного заряда. Это приближение позволяет проинтегрировать (5.5) в явном виде с небольшой погрешностью (см. раздел 4.5).
– прямоугольная аппроксимация объемного заряда. Это приближение позволяет проинтегрировать (5.5) в явном виде с небольшой погрешностью (см. раздел 4.5). .
. Постоянную интегрирования находим из граничных условий (рисунок 5.6, д). При ,
Постоянную интегрирования находим из граничных условий (рисунок 5.6, д). При ,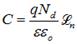


 при , (5.8)
при , (5.8)
 до нуля: .
до нуля: .

 ;
;  . (5.9)
. (5.9) .
.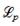
 . (5.10)
. (5.10)

 ; . (5.11)
; . (5.11)

 Последующее интегрирование (5.10) с граничным условием
Последующее интегрирование (5.10) с граничным условием  ,
,
 ;
;  .
.
 ; .
; .
 Из (5.11) и полной ширины ОПЗ,
Из (5.11) и полной ширины ОПЗ,  можно получить:
можно получить:
 ;
;  .
. . (5.12)
. (5.12) . (5.13)
. (5.13) , то формула (5.13) примет вид:
, то формула (5.13) примет вид:  . (5.13а)
. (5.13а)
 , (5.14)
, (5.14) см).
см). . (5.15)
. (5.15) .
. . (5.16)
. (5.16) Поскольку
Поскольку  (рисунок 5.7, а), то граничные условия можно записать в виде:
(рисунок 5.7, а), то граничные условия можно записать в виде: ;
;  ; (5.17)
; (5.17) ;
;  . (5.18)
. (5.18) После первого интегрирования (5.15) с (5.16) и второго условия (5.17) получим:
После первого интегрирования (5.15) с (5.16) и второго условия (5.17) получим: . (5.19)
. (5.19) . (5.20)
. (5.20) . (5.21)
. (5.21) ;
;  . (5.22)
. (5.22) Откуда следует толщина ОПЗ
Откуда следует толщина ОПЗ . (5.24)
. (5.24) .
. – парабола) больше, чем в ступенчатом (площадь
– парабола) больше, чем в ступенчатом (площадь  Прямое смещение p-n перехода соответствует такой полярности внешнего источника, при которой внешнее поле компенсирует контактное поле (рисунок 5.8, а). Внешнее поле полностью локализуется в ОПЗ, следовательно, результирующее поле при прямом смещении уменьшается, при этом уменьшается физическая толщина ОПЗ и понижается величина потенциального барьера.
Прямое смещение p-n перехода соответствует такой полярности внешнего источника, при которой внешнее поле компенсирует контактное поле (рисунок 5.8, а). Внешнее поле полностью локализуется в ОПЗ, следовательно, результирующее поле при прямом смещении уменьшается, при этом уменьшается физическая толщина ОПЗ и понижается величина потенциального барьера. .
. . (5.25)
. (5.25) , так как
, так как  ;
;  .
.
 в р-области, и
в р-области, и  в n-области.
в n-области. , и
, и  ; концентрация основных носителей в базах практически не меняется, в то время как концентрация неосновных значительно увеличивается:
; концентрация основных носителей в базах практически не меняется, в то время как концентрация неосновных значительно увеличивается: ;
;  .
.
 ;
; . (5.26)
. (5.26) ;
;  .
. ;
;  .
. .
. .
.
 ;
;  .
. ;
;  ,
,
 (рисунок 5.10, а).
(рисунок 5.10, а). ,
, – поток носителей через p-n переход.
– поток носителей через p-n переход.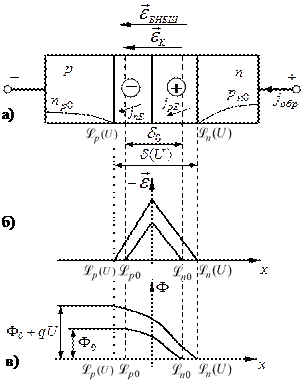 При обратном смещении внешнее поле направлено по контактному полю. Потенциальный барьер повышается, толщина ОПЗ увеличивается (эксклюзия основных носителей, внешнее поле отталкивает по обе стороны основные носители, расширяя слой объемного заряда неподвижных ионов доноров со стороны n- области и акцепторов со стороны p-области). Одновременно внешнее поле экстрагирует неосновные носители заряда с границы ОПЗ – квазинейтральная база, которые захватываются полем ОПЗ и перемещаются в другую базу, где они становятся основными и замыкают цепь обратного тока на источник (рисунок 5.11, а).
При обратном смещении внешнее поле направлено по контактному полю. Потенциальный барьер повышается, толщина ОПЗ увеличивается (эксклюзия основных носителей, внешнее поле отталкивает по обе стороны основные носители, расширяя слой объемного заряда неподвижных ионов доноров со стороны n- области и акцепторов со стороны p-области). Одновременно внешнее поле экстрагирует неосновные носители заряда с границы ОПЗ – квазинейтральная база, которые захватываются полем ОПЗ и перемещаются в другую базу, где они становятся основными и замыкают цепь обратного тока на источник (рисунок 5.11, а). .
. . (5.27)
. (5.27) , так как
, так как  .
. ;
; .
. При U = 1 В, и Т = 300 К,
При U = 1 В, и Т = 300 К,  .
.
 , а в n-базе концентрация дырок определяется
, а в n-базе концентрация дырок определяется  . На расстоянии
. На расстоянии 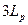 в n-базе квазиуровень
в n-базе квазиуровень  сливается с равновесным
сливается с равновесным  , так как на этом расстоянии тепловая генерация поддерживает равновесную концентрацию
, так как на этом расстоянии тепловая генерация поддерживает равновесную концентрацию  .
.

 . Это условие реализуется у монокристаллических полупроводников. Доля рекомбинации носителей в ОПЗ мала.
. Это условие реализуется у монокристаллических полупроводников. Доля рекомбинации носителей в ОПЗ мала. . Нет влияния контактов.
. Нет влияния контактов. ;
;  .
. ;
;  .
.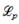

 , (рисунок 5.10, б).
, (рисунок 5.10, б). (рисунок 5.10, а),
(рисунок 5.10, а),  ,
, – темп тепловой генерации;
– темп тепловой генерации;  – темп тепловой рекомбинации.
– темп тепловой рекомбинации. .
. ) и стационарное условие
) и стационарное условие  , получим:
, получим: или
или  , (5.28)
, (5.28) – диффузионная длина ННЗ (дырок) в n-базе.
– диффузионная длина ННЗ (дырок) в n-базе. . Тогда (5.28) сводится к простому дифференциальному уравнению второго порядка,
. Тогда (5.28) сводится к простому дифференциальному уравнению второго порядка, ,
, .
. ,
,  . (5.29)
. (5.29) .
. .
. .
. ,
,




 ,
,  в начальных точках отсекают по оси x характерную величину распределения – диффузионную длину ННЗ.
в начальных точках отсекают по оси x характерную величину распределения – диффузионную длину ННЗ.
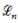
 . (5.31)
. (5.31) .
. , (5.32)
, (5.32) – плотность тока насыщения не зависит от приложенного напряжения.
– плотность тока насыщения не зависит от приложенного напряжения.
 ,
,  .
. .
. ;
;  ,
, . (5.33)
. (5.33) (рисунок 5. 16, а, б).
(рисунок 5. 16, а, б). ,
,  ,
, . (5.34)
. (5.34)
 .
. ,
,

 .
. . (5.35)
. (5.35) .
.