|
|
Механические колебания. Гармонические колебания.Затухающие колебания. Волны в упругой среде. Акустика.
1. Дифференциальное уравнение гармонических колебаний материальной точки:
где m – масса точки; k – коэффициент квазиупругой силы (k=ω2m ). 2. Уравнение гармонических колебаний:
где х – смещение колеблющейся точки от положения равновесия к моменту времени t; А – амплитуда колебания; Т – период колебаний; ω – круговая частота колебаний; φ – начальная фаза колебаний. 3. Скорость точки, совершающей гармоническое колебание:
4. Ускорение при гармоническом колебании:
5. Амплитуда А результирующего колебания, полученного при сложении двух колебаний с одинаковыми частотами, происходящих по одной прямой, определяется по формуле:
6. Начальная фаза φ результирующего колебания:
7. Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях с амплитудами А1 и А2 и начальными фазами φ1 и φ2:
8. Полная энергия материальной точки, совершающей гармонические колебания:
9. Период колебаний тела, подвешенного на пружине:
Период колебаний математического маятника:
Период колебаний физического маятника:
где J – момент инерции колеблющегося тела относительно оси колебаний; m – масса маятника; а – расстояние центра масс маятника от оси колебаний. Период крутильных колебаний тела, подвешенного на упругой нити:
где J – момент инерции тела относительно оси, совпадающей с упругой нитью; k – жесткость упругой нити, равная отношению упругого момента, возникающего при закручивании нити, к углу, на который нить закручивается. 10. Дифференциальное уравнение затухающих колебаний:
где β – коэффициент затухания. 11. Уравнение волны:
где ξ(x,t)- смещение точек среды с координатой x в момент t; ω – круговая частота; v – скорость распространения колебаний в среде или
k – волновое число. 12. Длина волны:
где Т – период колебаний; υ – частота колебаний. 13. Разность фаз колебаний двух точек среды, расстояние между которыми (разность хода) равно Δх:
14. Уравнение стоячей волны:
15. Фазовая скорость продольных волн в упругой среде: а) в твердых телах
E – модуль Юнга; ρ – плотность вещества. б) в газах
γ – показатель адиабаты; R – молярная газовая постоянная; Т – термодинамическая температура; μ – молярная масса; Р – давление газа. в) для жидкостей
16. Акустический эффект Доплера:
υ – частота звука воспринимаемого движущимся прибором или ухом; v – скорость звука в среде; Uпр – скорость прибора относительно среды; Uист – скорость источника звука относительно среды; υ0 – частота звука, испускаемого источником. 17. Амплитуда звукового давленя:
υ – частота звука; А – амплитуда колебаний частиц среды; v – скорость звука в среде; ρ – плотность среды. 18. Средняя объемная плотность энергии звукового поля:
19. Поток звуковой энергии:
где W – энергия, переносимая через данную поверхность за время t. 20. Интенсивность звука:
21. Связь мощности N и точечного изотропного источника звука с интенсивностью звука:
r – расстояние от источника звука до точки звукового поля, в которой определяется интенсивность. 22. Удельное акустическое сопротивление среды:
23. Акустическое сопротивление:
где S – площадь сечения участка акустического поля. 24. Уровень интенсивности звука (уровень звуковой мощности в децибелах):
где J0=1·10-12 Вт/м2 – условная интенсивность, соответствующая нулевому уровню интенсивности.
Задачи. 1. Уравнение колебаний точки имеет вид х = А · cos(t+ τ) , где ω=π · с-1 , τ=0,2. Определить период Т и начальную фазу φ колебаний. 2. Написать уравнение гармоническою колебательного движения с амплитудой 5 см, если в 1 мин совершается 150 колебании и начальная фаза колебании равна 45°. Начертить график этого движения. 3. Точка равномерно движется но окружности против часовой стрелки с периодом Т=6 с. Диаметр окружности равен 20 см. Написать уравнение движения проекции точки на ось X, проходящую через центр окружности, если в момент времени, принятый за начальный, проекция на ось Х равна нулю. Найти смещение X, скорость X, ускорение Х проекции точки в момент t=1 с. 4. Определить максимальные значения скорости и ускорения точки, совершающей гармонические колебания с амплитудой А=З см и циклической частотой 5. Уравнение движения точки дано в виде 6. Точка совершает колебания по закону х=А · cosωt, где А=5 см, ω=2 с-1. Определить ускорение точки в момент времени, когда ее скорость v=8 см/с. 7. К пружине подвешен груз массой m=10 кг. Зная, что пружина под влиянием силы в 10 Н растягивается на 1,5 см, определить период вертикальных колебаний. 8. Амплитуда гармонических колебаний материальной точки А=2 см, полная энергия колебаний W=3 · 10 Дж. При каком смещении от положения равновесия на колеблющуюся точку действует сила F=2,25 · 105 Н? |
|


















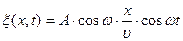 или
или
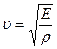
 или
или 
 - коэффициент сжатия.
- коэффициент сжатия.





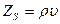

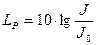
 .
. . Найти моменты времени, в которые достигаются максимальная скорость и максимальное ускорение.
. Найти моменты времени, в которые достигаются максимальная скорость и максимальное ускорение.