|
|
ТЕМЫ КУРСОВЫХ ПРОЕКТОВ (РАБОТ)Курсовые работы рабочим учебным планом не предусмотрены.
Учебно-методическое и информационное обеспечение дисциплины
МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
11. Методические рекомендации по организации изучения дисциплины
Дисциплина может читаться двумя модулями (первый модуль - разделы 1-4, второй модуль- разделы 5-8) соответственно в первом и втором семестрах обучения. (указываются рекомендуемые модули внутри дисциплины или междисциплинарные модули, в состав которых она может входить, образовательные технологии, а также примеры оценочных средств для текущего контроля успеваемости и промежуточной аттестации). Получение углубленных знаний по изучаемой дисциплине достигается за счет дополнительных часов к аудиторной работе - самостоятельной работы студентов. Выделяемые часы целесообразно использовать для знакомства с дополнительной учебной и научной литературой по проблематике дисциплины Промежуточным контролем знаний студентов в течение обучения являются контрольные работы (6) по ключевым темам читаемой дисциплины, по три в каждом семестре. Формой итогового контроля знаний студентов является письменный экзамен, в ходе которого оценивается уровень теоретических знаний и навыки решения практических задач. ФОНД ОЦЕНОЧНЫХ ЗНАНИЙ ТЕМЫ РЕФЕРАТОВ Рефераты рабочим учебным планом не предусмотрены.
КОНТРОЛЬНЫЕ РАБОТЫ Контрольная работа 1. 1. Вычислить определитель следующей матрицы
2. Дана следующая матрица
3. Найти решение следующей системы линейных уравнений методом Гаусса;
Контрольная работа 2. 1.Найти частные производные первого и второго порядка функции
2.Найти предел
3.Исследовать функцию и построить ее график:
Контрольная работа 3. 1.Вычислить интеграл
2.Решить дифференциальное уравнение:
3.Исследовать сходимость ряда:
Контрольная работа 4. 1.На сборочное предприятие поступили однотипные комплектующие с трех заводов в количестве: 30 с первого завода, 45 со второго и 25 с третьего. Вероятность качественного изготовления изделий на первом заводе 0.99, на втором заводе 0.98, а на третьем заводе 2.В городе имеется 4 оптовых базы. Вероятность того, что требуемого сорта товар отсутствует на этих базах, одинакова и равна 0.1; составить закон распределения числа баз, на которых искомый товар отсутствует в данный момент. 3. Найти выборочное среднее и несмещенную выборочную дисперсию на основе данного распределения выборки:
Контрольная работа 5. 1.Решить задачу линейного программирования геометрически:
2.Дать математическую постановку и решить следующую задачу планирования производства. Предприятие выпускает 2 вида продукции А и Б. На изготовление затрачиваются ресурсы трех видов В, Г, Д, запасы которых равны соответственно 30, 40 и 20 единиц. На изготовление единицы изделия А расходуется 3, 4 и 2 единиц ресурсов В, Г, Д соответственно, а на изготовление единицы изделия В – 5, 1 и 3 единиц соответственно. Реализация единицы А приносит прибыль к условных единиц, а единицы В – 5 условных единиц. Требуется определить план выпуска продукции А и В, обеспечивающий максимальную прибыль от реализации продукции. 3.Найти решение матричной антагонистической игры с матрицей
Контрольная работа 6. 1.Решить оптимизационную задачу методом множителей Лагранжа:
при ограничении
2.Известно, что звонки в торговый отдел организации поступают с интенсивностью (30+к) звонков в час. Среднее время разговора по телефону составляет 3 минуты. Определить минимальное число каналов телефона в этом отделе, чтобы в среднем из каждых 100 звонящих в отдел не менее 90 дозвонились. 3.В универсаме к узлу расчета поступает поток покупателей с интенсивностью (30+к) человек в час. Средняя продолжительность обслуживания кассиром одного покупателя равна 2 минуты. Определить минимальное число кассиров, при котором очередь не будет бесконечно расти, и характеристики обслуживания, имеющие место в этом случае.
ТЕСТЫ. Раздел 1. Задание 1. Выберите один из вариантов ответа: Определитель 1) 0; 2) 1; 3) 2; 4) 0,5 Задание 2.
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЗАЧЕТУ И ЭКЗАМЕНУ Раздел 1. 1. Виды матриц и операции над матрицами. 2. Определители квадратных матриц. Правило Сарруса вычисления определителей матриц третьего порядка. 3.Минор и алгебраическое дополнение элемента квадратной матрицы. Теорема Лапласа и схема ее применения для вычисления определителей квадратных матриц любого порядка. 4. Свойства определителей. 5. Обратная матрица. Необходимое и достаточное условие существования обратной матрицы. 6. Ранг матрицы. Теорема о ранге матрицы. 7. Метод Крамера решения системы линейных уравнений. 8. Метод Гаусса решения систем линейных уравнений. Теорема Кронекера-Копелли. Совместная, несовместная, неопределенная и определенная системы. 9. Системы линейных однородных уравнений. Фундаментальная система решений. 10. Модель Леонтьева многоотраслевой экономики. 11. Векторы на плоскости и в пространстве. Скалярное произведение векторов. 12. Векторное пространство. Линейная зависимость векторов. Линейное пространство. 13. Евклидово пространство. Норма вектора. Ортонормированный базис. 14. Линейные операторы и операции над ними. Собственные векторы и собственные значения линейного оператора. 15. Квадратичная форма. Приведение квадратичной формы к каноническому виду. Закон инерции квадратичных форм. Критерий Сильвестра установления знакоопределенности квадратичной формы. 16. Уравнение линии на плоскости. Уравнение прямой и различные формы ее математической записи. 17. Общее уравнение прямой и его исследование. Условие параллельности и перпендикулярности прямых. Расстояние от прямой до точки. 18. Кривые второго порядка. Окружность и эллипс. Каноническое уравнение эллипса. Характеристическое уравнение эллипса. 19. Гипербола и парабола. Характеристическое свойство гиперболы. Асимптоты гиперболы. Фокус и директриса параболы. Характеристическое свойство параболы. 20. Уравнения плоскости и прямой в пространстве. Общее уравнение плоскости. Условия параллельности и перпендикулярности плоскостей.
Раздел 2. 1. Понятие множества. Операции над множествами. Числовые множества. 2. Способы задания функции. Свойства функций. Обратная функция. Сложная функция. Элементарные функции. 3. Интерполирование функций. Применение функций в экономике и управлении. Функция полезности. Производственная функция. Функции выпуска, издержек, спроса, потребления и предложения. 4. Числовая последовательность. Предел числовой последовательности. Геометрический смысл предела числовой последовательности. 5. Предел функции в бесконечности и его геометрический смысл. Предел функции в точке и его геометрический смысл. 6. Бесконечно малые величины и бесконечно большие величины. Их связь. 7. Основные теоремы о пределах. Признаки существования предела. 8. Замечательные пределы. Задача о непрерывном начислении процентов. Способы вычисления пределов функций. 9. Непрерывность функции в точке. Точки разрыва функции и их классификация. 10. Свойства функций, непрерывных в точке. Свойства функций, непрерывных на отрезке. Теорема Вейерштрасса. Теорема Больцано-Коши. 11. Производная функции. Геометрический и механический смысл производной. Зависимость между непрерывностью функции и дифференцируемостью. 12. Основные правила дифференцирования. Производная сложной и обратной функции. Производные основных элементарных функций: логарифмической, показательной, степенной и тригонометрических. Производная неявной функции. 13. Производные высших порядков. Экономический смысл производной. Эластичность функции и ее свойства. Применение эластичности функций при анализе спроса и потребления. 14. Дифференциал функции. Его геометрический смысл. Свойства дифференциала функции. Дифференциалы высших порядков. 15. Теорема Ферма и ее геометрический смысл. 16. Теорема Ролля и ее геометрический смысл. 17. Теорема Лагранжа ее механический и геометрический смысл. 18. Правило Лопиталя и его применение к вычислению пределов функций. 19. Достаточное и необходимое условия возрастания функции. Достаточное условие убывания функции. 20. Экстремумы функции. Необходимое условие экстремума. Стационарные точки. Достаточные условия экстремума функции. 21. Выпуклость функции. Точки перегиба. Необходимое и достаточное условия перегиба графика функции. 22. Асимптоты графика функции. Вертикальная, горизонтальные и наклонная асимптоты графика функции. Общая схема исследования функций и построения их графиков. 23. Приложение производной в экономической теории. Закон убывающей доходности. Закон убывающей полезности. 24. Линия уровня функции двух переменных. Предел и непрерывность функции двух переменных. Частные производные и дифференциал функции двух переменных. Производная по направлению и градиент. 25. Необходимое и достаточное условия экстремума функции двух переменных. Глобальные экстремумы.
Раздел 3. 1. Двойной интеграл. Геометрический смысл двойного интеграла. 2. Первообразная функции и неопределенный интеграл. Свойства неопределенного интеграла. 3. Интегралы от основных элементарных функций. Методы нахождения неопределенных интегралов. Метод разложения. Метод замены переменной. Метод интегрирования по частям. Интегрирование простейших рациональных дробей. Интегрирование иррациональных и тригонометрических функций. 4. Определенный интеграл, его геометрический и экономический смысл. Достаточное условие интегрируемости функций. Свойства определенного интеграла. Теорема о среднем. 5. Определенный интеграл как функция верхнего предела. Формула Ньютона-Лейбница. Замена переменной и формула интегрирования по частям в определенном интеграле. 6. Геометрические приложения определенного интеграла. Вычисление площади плоской фигуры. Вычисление объемов тел вращения. 7. Несобственные интегралы с бесконечными пределами. Несобственные интегралы от неограниченных функций. 8. Использование понятия определенного интеграла в экономике. Расчет объема выпускаемой продукции за исследуемый временной период. Вычисление коэффициента Джини. Расчет дисконтированного дохода при оценке эффективностей капиталовложений. 9. Общее и частное решения дифференциального уравнения. Дифференциальные уравнения первого порядка. Теорема существования и единственности его решения. 10. Автономные дифференциальные уравнения. Неполные дифференциальные уравнения первого порядка. Дифференциальные уравнения с разделяющимися переменными. 11. Однородные дифференциальные уравнения первого порядка. Линейные дифференциальные уравнения первого порядка. Дифференциальные уравнения второго порядка, допускающие понижение порядка. 12. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами: однородные и неоднородные. Схема нахождения общего решения линейного неоднородного дифференциальные уравнения второго порядка. 13. Использование дифференциальные уравнения в экономической динамике. Модель естественного роста. Модель роста в условиях конкурентного рынка.
Раздел 4. 1. Числовые ряды. Сходящиеся и расходящиеся числовые ряды. Сумма ряда. 2.Свойства сходящихся числовых рядов. Необходимый признак сходимости числового ряда. 3. Гармонический ряд. Ряды с положительными членами. Признак сравнения. 4.Предельный признак сравнения. 5.Интегральный признак сходимости числового ряда. 6. Признак Даламбера сходимости знакочередующегося ряда. 7.Достаточный признак сходимости знакопеременного ряда. 8.Абсолютно сходящийся и условно сходящийся числовой ряд. 9. Степенные ряды. Область сходимости степенного ряда. 10.Теорема Абеля. Свойства степенных рядов. 11. Ряд Маклорена. Разложение функций в ряд Маклорена. 12.Ряд Тейлора. Применение рядов в приближенных вычислениях.
Раздел 5. 1. Виды случайных событий. Классическое определение вероятности событий. Свойства вероятности событий. Основные формулы комбинаторики. 2. Статистическая вероятность. Геометрическая вероятность. 3. Сумма и произведение событий. Теорема сложения вероятностей. Полная группа событий. Противоположные события. Условная вероятность. Теорема умножения вероятностей. Независимые события. 4. Формула полной вероятности. Формула Байеса. Формула Бернулли. 5. Дискретные и непрерывные случайные величины. Закон распределения дискретной случайной величины. 6. Биномиальное распределение. Распределение Пуассона. Простейший поток событий. Геометрическое и гипергеометрические распределения случайной величины. 7. Числовые характеристики дискретных случайных величин: математическое ожидание, дисперсия, среднее квадратическое отклонение. Их свойства. 8. Закон больших чисел. Неравенство Чебышева. Теорема Чебышева. Теорема Бернулли. 9. Функция распределения случайной величины и ее свойства. 10. Плотность распределения непрерывной случайной величины и ее свойства. 11. Закон равномерного распределения вероятности. 12. Числовые характеристики непрерывных случайных величин: математическое ожидание, дисперсия, среднее квадратическое отклонение. 13. Нормальный закон распределения. Вероятность попадания в заданный интервал нормальной случайной величины. Правило трех сигм. 14. Мода, медиана, асимметрия и эксцесс распределения. 15. Показательное распределение. 16. Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции. 17. Генеральная и выборочная совокупности. Виды выборок. Эмпирическая функция распределения. Полигон и гистограмма. 18. Статистические оценки параметров распределения. Несмещенные, состоятельные и эффективные оценки. 19. Выборочная средняя. Выборочная дисперсия, несмещенная выборочная дисперсия. 20. Доверительная вероятность и доверительный интервал. Доверительные интервалы для оценки математического ожидания нормального распределения и среднего квадратического отклонения. 21. Статистическая гипотеза. Нулевая и конкурирующая, простая и сложная гипотезы. Ошибки первого и второго рода. Критическая область. Область принятия гипотезы. Критические точки. Мощность критерия. 22. Сравнение дисперсий двух генеральных совокупностей. 23. Сравнение выборочной средней с гипотетической генеральной средней нормальной совокупности.
Раздел 6. 1. Каноническая задача линейного программирования. Сведение общей задачи линейного программирования к канонической. 2. Геометрический метод решения задач линейного программирования. 3. Симплексный метод решения задачи линейного программирования. Отыскание начального допустимого базисного решения. 4. Двойственные задачи линейного программирования. Связь решений двойственных задач. Экономическая интерпретация задачи, двойственной задаче об использовании ресурсов. 5. Экономико-математическая модель транспортной задачи. 6. Нахождение первоначального опорного плана транспортной задачи. Метод «северо-западного угла». Метод минимальной стоимости. 7. Метод потенциалов нахождения оптимального плана транспортной задачи. 8. Решение открытых транспортных задач. 9. Задача целочисленного программирования. Метод Гомори решения задач целочисленного программирования. 10. Задачи параметрического и стохастического программирования. 11. Матричные антагонистические игры. Платежная матрица. Нижняя и верхняя цена игры. 12. Решение игр в смешанных стратегиях. 13.Сведение матричной игры к задаче линейного программирования. 14. Игры с природой. Критерии Байеса, Сэвиджа, Вальда, Гурвица в играх с природой без проведения эксперимента. 15. Статистические игры с проведением экспериментов.
Раздел 7. 1. Нахождение условных экстремумов. Метод множителей Лагранжа. 2. Численные методы решения нелинейных оптимизационных задач. Метод покоординатного спуска. 3.Градиентный метод. 4.Метод Ньютона. 5. Общая постановка задачи динамического программирования. 6. Принцип оптимальности Беллмана. 7.Уравнения Беллмана. 8.Схема решения задачи динамического программирования. 9. Задача распределения средств между предприятиями. 10. Задача о замене оборудования.
Раздел 8. 1. Сетевая модель и ее основные элементы. 2. Порядок и правила построения сетевых графиков. 3. Упорядочение сетевого графика. Понятие о пути. 4. Временные параметры сетевых графиков. 5. Сетевое планирование в условиях неопределенности. 6. Анализ и оптимизация сетевого графика. 7. Классификация систем массового обслуживания. 8. Понятие марковского случайного процесса. 9. Уравнения Колмогорова для вероятностей состояний системы массового обслуживания. 10. Предельные вероятности состояний. Процесс гибели и размножения. 11. Основные характеристики систем массового обслуживания. 12. Системы массового обслуживания с отказами. 13. Системы массового обслуживания с неограниченной очередью и ограниченной очередью. 14. Оптимизация числа каналов в системе массового обслуживания. 15. Статическая детерминированная модель управления запасами без дефицита. Формула Уилсона. 16. Статическая детерминированная модель с дефицитом. 17. Стохастическая модель управления запасами.
[1] В ячейке указаны номера тем данного раздела |
|
 , где в этой и следующих задачах
, где в этой и следующих задачах  - номер студента в списке группы.
- номер студента в списке группы.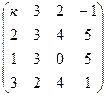 . Найти
. Найти  .
.
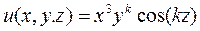 .
. .
. .
. .
. .
. .
.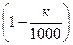 . Какова вероятность того, что случайно взятое изделие будет качественным?
. Какова вероятность того, что случайно взятое изделие будет качественным?

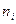
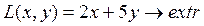
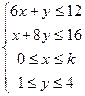
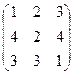
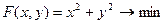
 .
. =0 при
=0 при  равном …
равном …