|
|
Занятие 4. Кинематика колебательного движения. Гармонические колебания. Сложение колебаний.Краткие теоретические сведения Основные формулы Уравнение гармонических колебаний
где Циклическая частота
Скорость точки, совершающей гармонические колебания
Ускорение точки, совершающей гармонические колебания
При сложении колебаний одного направления и одинаковой частоты: Результирующая амплитуда колебаний находится по формуле:
Начальная фаза результирующего колебания:
Дифференциальное уравнение гармонических колебаний материальной точки:
Полная энергия материальной точки, совершающей гармонические колебания:
Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях с амплитудами
Вопросы для ответа у доски: 1. Колебательное движение. Описание гармонического колебательного движения. Скорость и ускорение точки при гармонических колебаниях. Дайте определение колебательного движения и классификацию колебаний. Исследуйте одномерное гармоническое колебательное движение и приведите соответствующие графики. Укажите точки, где колеблющееся тело имеет наибольшую скорость и ускорение. 2. Векторные диаграммы. Установите связь между гармоническим колебанием материальной точки с амплитудой 3. Сложение колебаний одного направления. Биения. Приведите примеры сложения колебаний одного направления и запишите их уравнения колебаний. Сформулируйте постановку задачи. С помощью метода векторных диаграмм найдите геометрически результирующее колебание. Получите выражение для амплитуды и начальной фазы при сложении двух колебаний с одинаковой частотой. 4. Сложение взаимно перпендикулярных колебаний. Приведите примеры сложения двух взаимно перпендикулярных колебаний. Найдите уравнение траектории сложного колебания и рассмотрите случаи для различных начальных фаз. Покажите, как зависит траектория от частот исходных колебаний. Примеры решения задач: Задача 1. Гармоническое колебание материальной точки задано уравнением
отсюда Время
Скорость точки, совершающей колебание:
Отсюда
Ответ: Задача 2. Написать уравнение гармонического колебательного движения, если максимальное ускорение точки Решение: Запишем уравнение гармонических колебаний точки:
Ускорение точки, совершающей колебания определяется соотношениями:
максимальное ускорение: Отсюда амплитуда колебаний:
Вычисляя, находим:
Подставив в уравнение гармонических колебаний (1) числовые значения амплитуды и периода, получаем:
Используя условие, что при
Уравнение гармонического колебания точки получим, подставив значение начальной фазы колебаний:
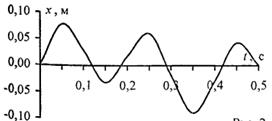
Ответ: Задача 3. Уравнения двух гармонических колебаний имеют вид Решение: Составим таблицу значений
Вопросы для самопроверки: 1. Какое движение называется колебательным? Какие колебания называются гармоническими; негармоническими? Приведите примеры. 2. Что такое фаза колебания и что она определяет? Что такое начальная фаза? 3. Дайте определение линейной и циклической частот. Как они связаны между собой? В каких единицах измеряются? 4. Что означает знак минус в соотношении, связывающем смещение и ускорение колеблющейся точки? 5. Как найти амплитуду скорости и ускорения? От каких величин они зависят? 6. Что такое векторная диаграмма? Изобразить на рисунке колебание и соответствующую векторную диаграмму. 7. В каких колебаниях должна участвовать точка, чтобы ее траекторией была прямая линия; окружность; эллипс? 8. Как образуются фигуры Лиссажу? 9. Прикаком условии два колебания максимально усиливают друг друга; ослабляют? 10. Когда возникают биения? Являются ли биения гармоническими колебаниями? 11. Как производится гармонический анализ сложного колебания? Задачи для самостоятельного решения: 1. Небольшой грузик совершает колебания по закону 2. Точка, совершающая гармонические колебания, в некоторый момент времени имеет смещение 4·10-2 м, скорость 0,05 м/с и ускорение 0,8 м/с2. Определите: а) амплитуду и период колебаний точки; б) фазу колебаний в рассматриваемый момент времени; в) максимальные скорость и ускорение точки; г) время прохождения пути, равного половине амплитуды колебаний при движении из положения равновесия (из крайней точки). 3. Точка участвует в двух взаимно перпендикулярных колебаниях, описываемых уравнениями 4. Уравнение движения точки дано в виде 5. Написать уравнение гармонического колебательного движения, если максимальное ускорение точки 6. Найти амплитуду
7. Найти амплитуду 8. Некоторая точка совершает колебания вдоль оси 9. Частица совершает гармонические колебания вдоль оси 10. Точка совершает гармонические колебания вдоль некоторой прямой с периодом 11. Частица совершает гармонические колебания вдоль оси 12. Точка движется в плоскости 13. Наибольшее смещение и наибольшая скорость точки, совершающей гармоническое колебание, равны соответственно 5 см и 12 см/с. а) Каково наибольшее ускорение? Б) Каковы скорость и ускорение точки в тот момент, когда смещение 3 см? 14. Конец ветви камертона колеблется с частотой 500 Гц и амплитудой 0,2мм. Определить: а) среднюю скорость при движении от крайнего положения к положению равновесия; б) среднюю скорость при прохождении 0,1мм, начиная от крайнего положения. 15.
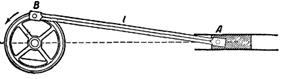 Во многих машинах (компрессор, водяной насос и т.п.) встречается механизм, схематически изображенный на Рис.1.4.2. При каком условии движение точки Во многих машинах (компрессор, водяной насос и т.п.) встречается механизм, схематически изображенный на Рис.1.4.2. При каком условии движение точки 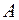 можно считать гармоническим колебанием, если точка можно считать гармоническим колебанием, если точка 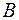 равномерно движется по окружности? равномерно движется по окружности?
16. а) Два одинаково направленных гармонических колебания одного периода с амплитудами 5 см и 7 см складываются в одно гармоническое колебание с амплитудой 9 см. Определить разность фаз складываемых колебаний. б) Наибольшая скорость первого колебания равна 50см/с. Определить наибольшую скорость результирующего колебания. 17. В помещении установлены два электродвигателя. Когда работает один из двигателей, некоторая точка пола совершает колебания с амплитудой 0,1мм и с частотой 1410 мин-1. Когда работает другой двигатель, та же точка пола совершает колебания с той же амплитудой и с частотой 1440мин-1. Как будет колебаться эта точка, если оба двигателя будут работать одновременно? 18. При сложении двух гармонических колебаний одного направления результирующее колебание точки имеет вид: 19. Написать уравнение результирующего колебания, получающегося в результате сложения двух взаимно перпендикулярных колебаний с одинаковой частотой Модуль 2. Динамика. Занятие 1. Законы Ньютона. Краткие теоретические сведения Основные формулы Уравнение движения материальной точки (второй закон Ньютона):
где Сила гравитационного взаимодействия (закон всемирного тяготения):
где Ускорение свободного падения у поверхности планет:
Ускорение свободного падения у поверхности Земли Ускорение свободного падения для тел, поднятых над Землей на высоту
Сила тяжести:
Сила упругости (закон Гука):
где Вопросы для ответа у доски: 1. Первый закон Ньютона. Инерциальные системы отсчета. Инерция и инертность. Масса. Единицы измерения массы. Сила. Измерение силы. Единицы измерения силы. 2. Второй закон Ньютона. Принцип независимости действия сил. Способы проявления сил. Классификация фундаментальных взаимодействий. Классификация сил в механике. Прямая и обратная задача механики. Расчет силы, действующей на материальную точку, если ее движение задано векторным, координатным или естественным способом. Второй закон Ньютона в общей форме. 3. Третий закон Ньютона. Границы применимости механики Ньютона. Какова роль законов Ньютона в механике? Сформулируйте третий закон Ньютона. Может ли нарушаться третий закон Ньютона? Импульс материальной точки? В каком виде можно сформулировать третий закон Ньютона, чтобы он всегда выполнялся? Примеры решения задач: Задача 1. Человек тянет груз за веревку, при этом веревка составляет с горизонталью угол Решение: Выберем систему отсчета таким образом, чтобы ось Все силы будут приложены в одной точке – центре груза (Рис. 2.1.1).
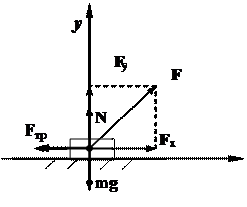
Спроектируем силу тяги на оси координат и найдем ее проекции
Составим систему уравнений, описывающих движение тела. Основное уравнение движения в векторной форме будет иметь вид:
В проекциях на оси на ось на ось Учитывая зависимость силы трения скольжения от силы реакции опоры
Выразив из второго уравнения силу реакции опоры
Так как
Ответ: Задача 2.Две гири с массами Решение: Сделаем чертеж (Рис.2.1.2) Весом нитью и растяжением можно пренебречь. Выберем элемент нити
сила натяжения нити во всех точках одинакова. Ускорения грузов тоже одинаковы из-за нерастяжимости нити грузы за одно и то же время проходят путь:
отсюда Запишем второй закон Ньютона для гири 1 и гири 2 в проекциях на ось
Решая систему уравнений, получим:
отсюда
Подставив числовые значения, получим:
Ответ: Задача 3. Автомобиль движется по выпуклому мосту радиусом кривизны Решение:
 Со стороны Земли на него действует сила тяжести Со стороны Земли на него действует сила тяжести 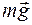 , со стороны моста – нормальная реакция опоры , со стороны моста – нормальная реакция опоры  и сила трения и сила трения 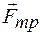 . .
Сцепление колес осуществляется за счет силы трения, направленной в сторону движения по касательной к поверхности моста. По второму закону динамики:
так как ускорение максимально, то и сила трения максимальна:
По нормали к траектории действуют две силы: Модуль равнодействующей, равный разности сил
Решая совместно уравнения (1) и (2) относительно касательного ускорения, получим:
Вычисляя, находим касательное ускорение равно:
Ответ: Вопросы и задания для самопроверки: 1. Что изучает динамика? 2. Сформулируйте первый закон Ньютона. В чем состоит физическое содержание этого закона? Какие системы отсчета называются инерциальными? 3. Что означают термины “инерция” и “инертность”? Что такое масса? Как устанавливаются единицы измерения массы? Как измеряется масса? 4. Что такое сила и как она измеряется? Как устанавливаются единицы измерения силы? Дайте определение этих единиц. 5. Что должно быть указано для каждой силы при решении задач? 6. Сформулируйте второй закон Ньютона. 7. В чем заключается принцип независимости действия сил? Какие следствия вытекают из этого принципа? 8. Каковы способы проявления сил? 9. Какие фундаментальные взаимодействия известны науке в настоящее время? Как классифицируются силы в механике? 10. Сформулируйте прямую и обратную задачи динамики. Как найти силу, действующую на материальную точку, если ее движение задано векторным, координатным или естественным способом? 11. Точка движется криволинейно. Как направлена сила, действующая на нее? Какова роль нормальной и тангенциальной составляющих силы? Как будет двигаться точка при отсутствии одной из составляющих? 12. Сформулируйте третий закон Ньютона. Может ли нарушаться третий закон Ньютона? 13. Что называют импульсом материальной точки? 14. Сформулируйте второй закон Ньютона в наиболее общей форме. 15. В каком виде можно сформулировать третий закон Ньютона, чтобы он всегда выполнялся? 16. Как экспериментально проверяются законы Ньютона? Являются ли они точными или приближенными? Есть ли границы применимости механики Ньютона? 17. Какова роль законов Ньютона в механике? Задачи для самостоятельного решения: 1. Аэростат, имеющий вместе с балластом массу 2. К потолку кабины лифта массой 3.
 Через неподвижный блок переброшен легкий нерастяжимый тросик, к одному концу которого привязано Через неподвижный блок переброшен легкий нерастяжимый тросик, к одному концу которого привязано 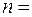 10 одинаковых грузиков. За свободный конец тросика тянут с силой 10 одинаковых грузиков. За свободный конец тросика тянут с силой  9,8 Н, и вся система находится в равновесии (Рис.2.1.4). В некоторый момент сила тяги начинает изменяться по закону 9,8 Н, и вся система находится в равновесии (Рис.2.1.4). В некоторый момент сила тяги начинает изменяться по закону 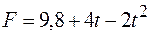 (Н) до значения (Н) до значения 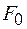 . Какую максимальную скорость будут иметь грузы в процессе движения? Какова должна быть минимальная прочность нитей, соединяющих грузы, чтобы не произошло разрыва при движении системы? . Какую максимальную скорость будут иметь грузы в процессе движения? Какова должна быть минимальная прочность нитей, соединяющих грузы, чтобы не произошло разрыва при движении системы?
4. Маляр работает в подвесном кресле. Масса маляра 72 кг, масса кресла 12 кг. С какой силой маляр должен подтягивать свободный конец веревки, чтобы подняться на высоту 3 м за 2 с? С какой силой маляр будет давить на кресло во время движения? На блок действует сила трения 30 Н. 5.
 ому концу нити, пропущенной через блоки, прикреплен груз массой ому концу нити, пропущенной через блоки, прикреплен груз массой  60 кг, на подвижном блоке висит груз массой 60 кг, на подвижном блоке висит груз массой  90 кг. В некоторый момент времени грузы находились на одном уровне, затем были предоставлены самим себе. Определите: время, в течение которого расстояние между грузами станет равным 2 м; показание динамометра при движении грузов. 90 кг. В некоторый момент времени грузы находились на одном уровне, затем были предоставлены самим себе. Определите: время, в течение которого расстояние между грузами станет равным 2 м; показание динамометра при движении грузов.
6. Автомобиль массой 1500 кг двигался по выпуклому мосту, имеющему форму дуги окружности с центральным углом 600. При въезде на мост скорость автомобиля была вдвое больше, чем при съезде с моста. Тангенциальное ускорение автомобиля 3,7 м/с2 . Определите максимальную силу давления автомобиля на мост. 7. Стальная проволока некоторого диаметра выдерживает силу натяжения 8. К нити подвешена гиря. Если поднимать гирю с ускорением 9. Тело массой 10. Уравнение движения пути 11. Какой угол 12. Две гири с массами 13. Невесомый блок укреплен на конце стола. Гири 1 и 2 одинаковой массы 14. 15.
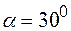 с горизонтом. Отношение масс тел с горизонтом. Отношение масс тел 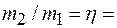 2/3. Коэффициент трения между телом и плоскостью 2/3. Коэффициент трения между телом и плоскостью 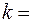 0,1. Массы блока и нити пренебрежимо малы. Найти модуль и направление ускорения тела 0,1. Массы блока и нити пренебрежимо малы. Найти модуль и направление ускорения тела 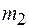 , если система пришла в движение из состояния покоя. , если система пришла в движение из состояния покоя.
16.
 Небольшое тело Небольшое тело  начинает скользить по наклонной плоскости из точки, расположенной над вертикальным упором начинает скользить по наклонной плоскости из точки, расположенной над вертикальным упором 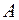 (Рис.2.1.7). Коэффициент трения между телом и наклонной плоскостью (Рис.2.1.7). Коэффициент трения между телом и наклонной плоскостью 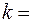 0,14. При каком значении угла 0,14. При каком значении угла  время соскальзывания будет наименьшим? время соскальзывания будет наименьшим?
17. Небольшое тело 18. Автомашина движется с постоянным тангенциальным ускорением 19. Груз, масса которого равна 1 кг, подвешенный на динамометре, поднимается сначала ускоренно, затем равномерно и, наконец, замедленно, после чего он таким же образом опускается. Абсолютная величина ускорения во всех случаях постоянна и равна 0,5 м/с2 . Что показывает динамометр в различные моменты движения? |
|
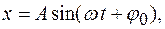
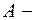 амплитуда колебаний,
амплитуда колебаний,  циклическая частота,
циклическая частота,  время,
время, 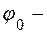 начальная фаза колебаний,
начальная фаза колебаний,  фаза колебаний.
фаза колебаний.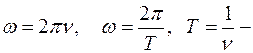 период колебаний.
период колебаний.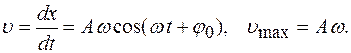
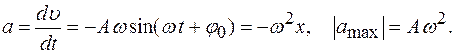
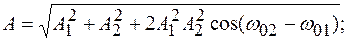
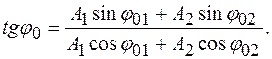
 0.
0.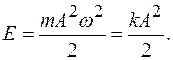
 и
и  и начальными фазами
и начальными фазами  и
и 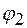 :
: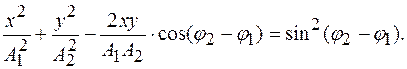
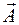 с угловой скоростью, равной частоте колебательного движения. Дайте соответствующий рисунок.
с угловой скоростью, равной частоте колебательного движения. Дайте соответствующий рисунок. м. Определить момент времени, при котором точка будет находиться в положении равновесия и максимальную скорость движения.
м. Определить момент времени, при котором точка будет находиться в положении равновесия и максимальную скорость движения.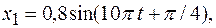 т.к. по условию
т.к. по условию  , то
, то 
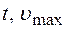
 где
где 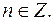
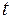 равно:
равно: при
при  0,075 с.
0,075 с. .
. 8·3,14·0,075 м/с=1,88 м/с.
8·3,14·0,075 м/с=1,88 м/с. 1,88 м/с.
1,88 м/с. 49,3 см/с2, период колебаний
49,3 см/с2, период колебаний  2 с и смещение точки от положения равновесия в начальный момент времени
2 с и смещение точки от положения равновесия в начальный момент времени  25 мм.
25 мм.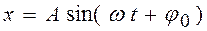 . (1)
. (1)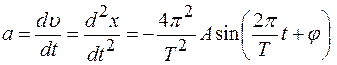 ,
,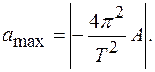
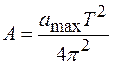 .
. см=5 см.
см=5 см.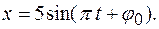
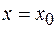 найдем начальную фазу колебаний:
найдем начальную фазу колебаний: , отсюда
, отсюда  ,
, 
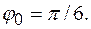
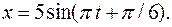
 и
и  (
( 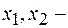 в см). Построить график этих колебаний. Сложив графически эти колебания, построить график результирующего колебания.
в см). Построить график этих колебаний. Сложив графически эти колебания, построить график результирующего колебания.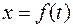 для данных колебаний и построим их графики (Рис.1.4.1а). Затем, сложив значения
для данных колебаний и построим их графики (Рис.1.4.1а). Затем, сложив значения 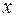 , соответствующие одним и тем же значениям
, соответствующие одним и тем же значениям 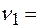 2 Гц;
2 Гц; 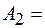 0,06 м;
0,06 м; 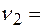 5 Гц.
5 Гц. (см). Определите: а) период, начальную фазу колебаний, максимальные скорость и ускорение груза; б) промежутки времени от начала отсчета движения, через которые грузик будет проходить положение равновесия. Установите закон изменения скорости и ускорения грузика в зависимости от его смещения.
(см). Определите: а) период, начальную фазу колебаний, максимальные скорость и ускорение груза; б) промежутки времени от начала отсчета движения, через которые грузик будет проходить положение равновесия. Установите закон изменения скорости и ускорения грузика в зависимости от его смещения. и
и  а) Постройте траекторию движения точки и укажите направление ее движения. б) Найдите максимальные скорость и ускорение точки.
а) Постройте траекторию движения точки и укажите направление ее движения. б) Найдите максимальные скорость и ускорение точки.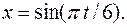 Найти моменты времени
Найти моменты времени  в которые достигаются максимальная скорость и максимальное ускорение.
в которые достигаются максимальная скорость и максимальное ускорение. гармонического колебания, полученного от сложения одинаково направленных колебаний, данных уравнениями:
гармонического колебания, полученного от сложения одинаково направленных колебаний, данных уравнениями: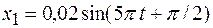 (м),
(м),  (м).
(м).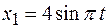 (см) и
(см) и 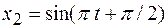 (см). Написать уравнение результирующего колебания.
(см). Написать уравнение результирующего колебания. Найти: а) амплитуду и период колебаний; изобразить график
Найти: а) амплитуду и период колебаний; изобразить график  ; б) проекцию скорости
; б) проекцию скорости  как функцию координаты
как функцию координаты 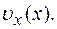
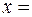 0, Частота колебаний
0, Частота колебаний  4,00 с-1. В некоторый момент координата частицы
4,00 с-1. В некоторый момент координата частицы 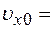 100 см/с. Найти координату
100 см/с. Найти координату  10 см. Найти среднюю скорость точки за время, в течение которого она проходит путь
10 см. Найти среднюю скорость точки за время, в течение которого она проходит путь 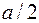 : а) из крайнего положения; б) из положения равновесия.
: а) из крайнего положения; б) из положения равновесия.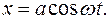 Считая вероятность
Считая вероятность 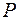 нахождения частицы в интервале от
нахождения частицы в интервале от  до
до  равной единице, найти зависимость от
равной единице, найти зависимость от 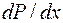 , где
, где  вероятность нахождения частицы в интервале от
вероятность нахождения частицы в интервале от 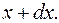 Изобразить график
Изобразить график 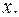
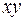 по закону
по закону  где
где  постоянные. Найти: а) уравнение траектории точки
постоянные. Найти: а) уравнение траектории точки  и направление ее движения по этой траектории; б) ускорение
и направление ее движения по этой траектории; б) ускорение 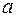 точки в зависимости от ее радиус-вектора
точки в зависимости от ее радиус-вектора 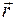 относительно начала координат.
относительно начала координат.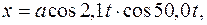 где
где  5Гц и одинаковой начальной фазой
5Гц и одинаковой начальной фазой  Амплитуды колебаний равны
Амплитуды колебаний равны  0,10 м и
0,10 м и 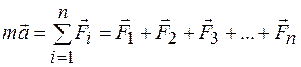 или
или 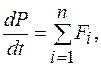
 масса,
масса,  сила,
сила, 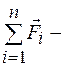 геометрическая сумма всех сил, действующих на материальную точку.
геометрическая сумма всех сил, действующих на материальную точку.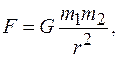
 6,67·10-11м3/(кг·с2) – гравитационная постоянная,
6,67·10-11м3/(кг·с2) – гравитационная постоянная,  расстояние между материальными точками.
расстояние между материальными точками. где М – масса планеты,
где М – масса планеты,  радиус планеты.
радиус планеты.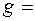 9,81м/с2.
9,81м/с2. :
:
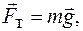
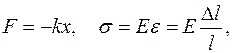
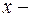 изменение размеров тела (удлинение),
изменение размеров тела (удлинение),  коэффициент упругости,
коэффициент упругости, 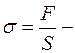 напряжение в теле, возникающее за счет действия силы,
напряжение в теле, возникающее за счет действия силы, 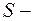 площадь поперечного сечения тела,
площадь поперечного сечения тела, 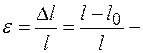 относительное удлинение,
относительное удлинение,  модуль Юнга (модуль упругости).
модуль Юнга (модуль упругости). 450, а коэффициент трения груза о горизонтальную поверхность, по которой он движется 0,01. Определите ускорение груза, если его масса 40кг, а сила, приложенная человеком к веревке, равна 50Н.
450, а коэффициент трения груза о горизонтальную поверхность, по которой он движется 0,01. Определите ускорение груза, если его масса 40кг, а сила, приложенная человеком к веревке, равна 50Н.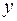 была к ней перпендикулярна. Груз будем считать достаточно малым, чтобы его можно принять за материальную точку.
была к ней перпендикулярна. Груз будем считать достаточно малым, чтобы его можно принять за материальную точку. и
и 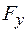 :
: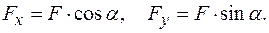
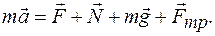
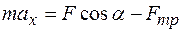 ;
;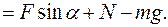
 , получим систему уравнений:
, получим систему уравнений: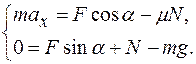
 и, подставив в первое уравнение, получим:
и, подставив в первое уравнение, получим: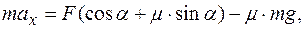
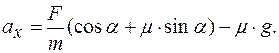
 то, подставив числовые значения, находим:
то, подставив числовые значения, находим: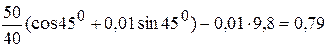 м/с2.
м/с2. 2 кг и
2 кг и  1 кг соединены нитью и перекинуты через невесомый блок. Найти ускорение
1 кг соединены нитью и перекинуты через невесомый блок. Найти ускорение 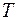 . Трением в блоке пренебречь.
. Трением в блоке пренебречь. . Запишем уравнение движения в проекции на ось
. Запишем уравнение движения в проекции на ось 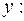
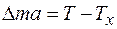 , так как
, так как 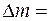 0, то
0, то 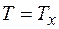 ,
,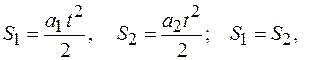
 Однако направления векторов
Однако направления векторов  и
и  противоположны.
противоположны.

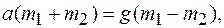
 , (3).
, (3). сила натяжения нити:
сила натяжения нити: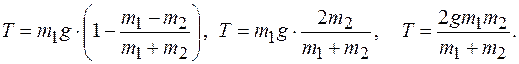
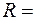 40 м. Какое максимальное ускорение в горизонтальном направлении может развивать автомобиль на вершине моста, если его скорость в этой точке равна 54 км/ч (15м/с)? Коэффициент трения колес автомобиля о мост равен
40 м. Какое максимальное ускорение в горизонтальном направлении может развивать автомобиль на вершине моста, если его скорость в этой точке равна 54 км/ч (15м/с)? Коэффициент трения колес автомобиля о мост равен 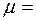 0,6.
0,6.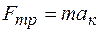 ,
, . (1)
. (1) и
и 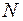 , сообщает автомобилю ускорение, направленное к центру окружности. По второму закону Ньютона для проекций сил и ускорений на нормаль к траектории на вершине моста:
, сообщает автомобилю ускорение, направленное к центру окружности. По второму закону Ньютона для проекций сил и ускорений на нормаль к траектории на вершине моста: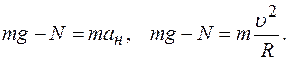 (2)
(2)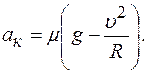
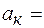 0,6·(9,8-152/40) м/с2=2,5 м/с2.
0,6·(9,8-152/40) м/с2=2,5 м/с2. подвешен идеально упругий шарик массой
подвешен идеально упругий шарик массой  . Шарик находится на расстоянии
. Шарик находится на расстоянии  от пола. Под действием силы
от пола. Под действием силы  кабина начинает подниматься ускоренно. Чему равно натяжение нити, которой шарик привязан к потолку кабины? Через сколько времени шарик достигнет пола, если нить внезапно оборвется? На какую высоту над полом подскочит шарик после удара?
кабина начинает подниматься ускоренно. Чему равно натяжение нити, которой шарик привязан к потолку кабины? Через сколько времени шарик достигнет пола, если нить внезапно оборвется? На какую высоту над полом подскочит шарик после удара? 2 м/с2, то сила натяжения нити
2 м/с2, то сила натяжения нити  будет вдвое меньше той силы натяжения
будет вдвое меньше той силы натяжения  , при которой нить разорвется. С каким ускорением
, при которой нить разорвется. С каким ускорением 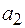 надо поднимать гирю, чтобы нить разорвалась?
надо поднимать гирю, чтобы нить разорвалась?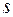 от времени
от времени 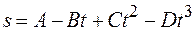 , где
, где 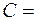 5 м/с2 и
5 м/с2 и  1 м/с3 . Найти силу
1 м/с3 . Найти силу  , где
, где 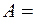 5 см и
5 см и 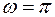 рад/с. Найти силу
рад/с. Найти силу 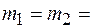 1 кг соединены нитью и перекинуты через блок. Коэффициент трения гири 2 о стол
1 кг соединены нитью и перекинуты через блок. Коэффициент трения гири 2 о стол  Частица движется вдоль оси
Частица движется вдоль оси  , где
, где 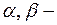 положительные постоянные. В момент времени
положительные постоянные. В момент времени  . Найти угол между вертикалью и радиусом-вектором, характеризующим положение тела
. Найти угол между вертикалью и радиусом-вектором, характеризующим положение тела  0,62м/с2 по горизонтальной поверхности, описывая дугу радиуса
0,62м/с2 по горизонтальной поверхности, описывая дугу радиуса