|
|
Занятие 6. Механика твердого тела. Динамика вращательного движения.Краткие теоретические сведения Основные формулы Момент инерции относительно оси вращения материальной точки:
твердого тела, состоящего из материальных точек:
Моменты инерции некоторых тел правильной геометрической формы
Теорема Штейнера:
где Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси:
где Момент силы
где Момент количества движения (импульса):
Закон сохранения момента импульса взаимодействующих тел:
Работа постоянного момента силы
где Мгновенная мощность, развиваемая при вращении тела:
Кинетическая энергия вращающегося тела:
Вопросы для ответа у доски: 1. Момент импульса системы материальных точек и его связь с моментом внешних сил. Используя второй закон Ньютона для материальной точки, выведите уравнение, связывающее момент импульса системы материальных точек с моментами внешних сил, действующих на данную систему. Рассмотрите движение системы под действием центральных сил и получите закон сохранения момента импульса системы. Приведите примеры проявления этого закона. 2. Второй закон Ньютона для вращательного движения твердого тела. Примените полученное выше выражение для момента импульса произвольно движущейся системы материальных точек к вращательному движению абсолютно твердого тела и выведите основное уравнение динамики вращательного движения. Сравните его с соответствующим уравнением для поступательного движения твердого тела. Приведите примеры вращательного движения тел, на которые действуют внешние силы, момент которых относительно оси вращения равен нулю. 3. Теорема Штейнера. Вычисление моментов инерции тел. Приведите примеры вычисления моментов инерции тел простой формы: стержня, тонкостенного цилиндра (обода), сплошного диска, шара. Выведите теорему Штейнера и покажите полезность ее применения. 4. Гироскоп. Дайте понятие о гироскопах с одной неподвижной точкой, с закрепленной осью и со свободной осью вращения. На примере одного из них рассмотрите поведение гироскопа под действием внешних сил. Покажите на примерах использование гироскопического эффекта и учета действия гироскопических сил. Примеры решения задач: Задача 1. Фигурист, вращаясь вокруг своей оси, прижимает руки как можно ближе к телу, и его момент инерции уменьшается до
Перепишем векторное уравнение (1) в скалярном виде:
Выразим угловую скорость через период вращения фигуриста:
Подставив (3) в уравнение (2), находим:
Вычисляя, находим момент инерции фигуриста:
Ответ: Задача 2. Какую работу нужно произвести, чтобы маховику массой
Момент инерции
Угловая скорость вращения маховика:
Подставив (2) и (3) в уравнение (1), получим:
учитывая, что
Проверим размерность:
Подставив числовые данные, получим:
Ответ: Задача 3. Колесо, вращаясь равнозамедленно, уменьшило за время Решение: Переведем числовые данные в систему СИ:
отсюда Угловое ускорение:
Подставив числовые значения, получим:
Момент сил торможения Ответ: Вопросы и задания для самопроверки: 1. Как определяется момент силы относительно точки относительно оси? 2. Как определяется момент импульса материальной точки относительно некоторой точки; относительно оси? 3. При каком условии выполняется закон сохранения момента импульса материальной точки? 4. Что такое число степеней свободы? Сколько степеней свободы имеют: материальная точка, движущаяся на плоскости; две жестко связанные свободные материальные точки; свободное твердое тело? Сколько дифференциальных уравнений движения надо составить для полного описания некоторой системы материальных точек? Приведите примеры. 5. Какое движение твердого тела называется поступательным? Приведите примеры. Почему при поступательном движении тела достаточно изучить движение одной его точки? Отличается ли второй закон Ньютона для материальной точки и поступательно движущегося тела? 6. Как определяется кинетическая энергия вращающегося тела? 7. По горизонтальной плоскости катится диск радиусом 8. Что называется моментом инерции тела и от чего он зависит? Почему момент инерции тела равен сумме моментов инерции его отдельных частей? Сколько моментов инерции может иметь данное тело? 9. Какое вращение тела называется свободным? Чем отличается свободное вращение вокруг свободной оси и вращение вокруг оси, не являющейся свободной? Какие из свободных осей устойчивы? 10. С наклонной плоскости скатываются два цилиндра одинакового радиуса и массы, но один полый, а другой сплошной. Какой из них скатится быстрее? 11. Дайте определение мгновенной и свободной осей вращения. Приведите примеры движения тел, имеющих указанные оси вращения. 12. Как возникает прецессия гироскопа? От чего зависит скорость прецессии? Задачи для самостоятельного решения: 1. Вал в виде сплошного цилиндра массой m1=10 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой m2= 2 кг. С каким ускорением а будет опускаться гиря, если ее предоставить самой себе? 2. Платформа в виде диска радиусом R= 1,5 м и массой m1=180 кг вращается по инерции около вертикальной оси с частотой n=10 мин-1. В центре платформы стоит человек массой m2=60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы. 3. Два маленьких шарика массой m=10 г каждый скреплены тонким невесомым стержнем длиной l=20 см. Определить момент инерции J системы относительно оси, перпендикулярной стержню и проходящей через центр масс. 4. Определить момент инерции J тонкого однородного стержня длиной l=30см и массой m=100 г относительно оси перпендикулярной стержню и проходящей через: 1) его конец; 2) его середину; 3) точку, отстоящую от конца стержня на 1/3 его длины. 5. Определить момент инерции J тонкого однородного стержня длиной l=60см и массой m=100 г относительно оси, перпендикулярной стержню и проходящей через точку стержня, удаленную на а=20 см от одного из его концов. 6. Найти момент инерции J тонкого однородного кольца радиусом R=20 см и массой т=100 г относительно оси, лежащей в плоскости кольца и проходящей через его центр. 7. Определить момент инерции J кольца массой m=50 г и радиусом R=10 см относительно оси, касательной к кольцу. 8. Диаметр диска d=20 см, масса m=800 г. Определить момент инерции J диска относительно оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. 9. Тонкий однородный стержень длиной l=50 см и массой m=400 г вращается с угловым ускорением ε=3 рад/с2 около оси, проходящей перпендикулярно стержню через его середину. Определить вращающий момент М. 10. На горизонтальную ось насажены маховик и легкий шкив радиусом R=5см. На шкив намотан шнур, к которому привязан груз массой m=0,4кг. Опускаясь равноускоренно, груз прошел путь S=1,8 м за время t=3 с. Определить момент инерции J маховика. Массу шкива считать пренебрежимо малой. 11. Вал массой m=100 кг и радиусом R=5 см вращался с частотой n=8 с-1. К цилиндрической поверхности прижали тормозную колодку с силой F=40Н, под действием которой вал остановился через t=10 с. Определить коэффициент трения 12. Через блок, имеющий форму диска, перекинут шнур. К концам шнура привязали грузики массой m1=100 г и m2=110 г. С каким ускорением а будут двигаться грузики, если масса m блока равна 400 г? Трение при вращении блока ничтожно мало. 13. Через неподвижный блок массой m=0,2 кг перекинут шнур, к концам которого подвесили грузы массами m1=0.3 кг и m2= 0,5 кг. Определить силы натяжения Т1 и Т2 шнура по обе стороны блока во время движения грузов, если масса блока равномерно распределена по ободу. 14. На краю горизонтальной платформы, имеющей форму диска радиусом R=2 м, стоит человек массой т1=80 кг. Масса m2 платформы равна 240кг. Платформа может вращаться вокруг вертикальной оси, проходящей через ее центр. Пренебрегая трением, найти, с какой угловой скоростью ω будет вращаться платформа, если человек будет идти вдоль ее края со скоростью 15. Платформа в виде диска радиусом R=1м вращается по инерции с частотой п1=6 мин-1. На краю платформы стоит человек, масса m которого равна 80 кг. С какой частотой п будет вращаться платформа, если человек перейдет в ее центр? Момент инерции J платформы равен 120кг·м2. Момент инерции человека рассчитывать, как для материальной точки. 16. Маховик вращается по закону, выраженному уравнением 17. Со шкива диаметром d=0,48 м через ремень передается мощность N=9кВт. Шкив вращается с частотой n=240 мин-1. Сила натяжения Т1 ведущей ветви ремня в два раза больше силы натяжения T2 ведомой ветви. Найти силы натяжения обеих ветвей ремня. 18. Для определения мощности двигателя на его шкив диаметром d=20 см накинули ленту. К одному концу ленты прикреплен динамометр, к другому подвесили груз. Найти мощность N двигателя, вращающего с частотой n=24 с-1. Масса m груза равна 1кг и показание динамометра F=24 Н. 19. Маховик в виде диска массой т=80 кг и радиусом R=30 см находится в состоянии покоя. Какую работу А1 нужно совершить, чтобы сообщить маховику частоту n=10 с-1? Какую работу А2 пришлось бы совершить, если бы при той же массе диск имел меньшую толщину, но вдвое больший радиус? 20. Кинетическая энергия T вращающегося маховика равна 1 кДж. Под действием постоянного тормозящего момента маховик начал вращаться равнозамедленно и, сделав N=80 оборотов, остановился. Определить момент М силы торможения. 21. Маховик, момент инерции J которого равен 40 кг·м2, начал вращаться равноускоренно из состояния покоя под действием момента силы М=20Н·м. Вращение продолжалось в течение t=10 с. Определить кинетическую энергию T, приобретенную маховиком. 22. Сплошной цилиндр массой т=4 кг катится без скольжения до горизонтальной поверхности. Линейная скорость 23. К ободу колеса радиусом R=0.5 м и массой m=50 кг приложена касательная сила Fk=98,1 Н. Найти угловое ускорение 24. Вентилятор вращается с частотой 25. Однородный диск радиусом R=0,2 м и массой m=5 кг вращается вокруг оси, проходящей через его центр перпендикулярно к его плоскости. Зависимость угловой скорости ω вращения диска от времени t дается уравнением ω=Bt, где В=8 рад/с2. Найти касательную силу, приложенную к ободу диска. Трением пренебречь. 26. Маховое колесо, момент инерции которого J=245 кг/м2, вращается с частотой 27. Найти линейные скорости 28. Маховик в виде сплошного диска, момент инерции которого J=150 кг м2, вращается с частотой 29. С какой силой следует прижать тормозную колодку к колесу, вращающемуся с частотой n1=30 об/с, для его остановки в течение t=20 с, если масса колеса распределена по ободу и равна m=10 кг, диаметр колеса d=20см? Коэффициент трения между колодкой и ободом колеса |
|
 где
где  масса точки,
масса точки,  расстояние до оси вращения;
расстояние до оси вращения;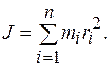
 и массой
и массой 






 момент инерции тела, относительно оси, проходящей через центр тяжести тела параллельно заданной оси;
момент инерции тела, относительно оси, проходящей через центр тяжести тела параллельно заданной оси;  расстояние между осями;
расстояние между осями;  ,
, момент вращающей силы, действующий на тело в течение времени
момент вращающей силы, действующий на тело в течение времени 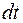 ;
;  момент инерции тела;
момент инерции тела;  угловое ускорение.
угловое ускорение. :
: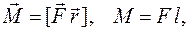
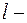 плечо силы (перпендикуляр, опущенный от оси вращения на линию действия силы),
плечо силы (перпендикуляр, опущенный от оси вращения на линию действия силы),  модуль силы.
модуль силы. где
где 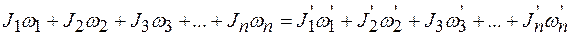
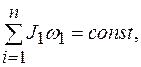
 , действующего на вращающееся тело:
, действующего на вращающееся тело: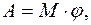
 угол поворота тела.
угол поворота тела.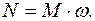
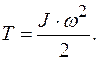
 =3,3 кг·м2 . При этом период вращения фигуриста уменьшается от
=3,3 кг·м2 . При этом период вращения фигуриста уменьшается от  =0,45с до
=0,45с до  =0,35с. Определите момент инерции
=0,35с. Определите момент инерции 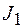 .
. 3,3 кг·м2
3,3 кг·м2
 0,45 с
0,45 с
 0,35 кг·м2
0,35 кг·м2


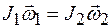 , (1)
где
, (1)
где 
 моменты импульса фигуриста до и после прижимания рук.
моменты импульса фигуриста до и после прижимания рук.
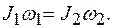 (2)
(2) (3)
(3) , отсюда
, отсюда 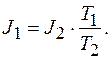
 3,3·0,45/0,35 кг·м2 =4,2 кг·м2.
3,3·0,45/0,35 кг·м2 =4,2 кг·м2. 0,6 т, распределенной по ободу диаметром
0,6 т, распределенной по ободу диаметром  1,6 м, сообщить вращение с частотой
1,6 м, сообщить вращение с частотой  240 об/мин.
240 об/мин. .
Кинетическая энергия вращения маховика:
.
Кинетическая энергия вращения маховика:
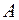
 (1)
(1) маховика радиусом
маховика радиусом  (2)
(2) (3)
(3)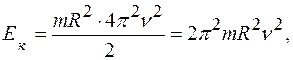
 получим:
получим: ,
, 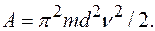
 1 кг·м2·с-2=1 Н·м=1 Дж.
1 кг·м2·с-2=1 Н·м=1 Дж.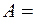 3,142·600·1,62·42/2 Дж=121155 Дж=121,2 кДж.
3,142·600·1,62·42/2 Дж=121155 Дж=121,2 кДж. 1 мин частоту вращения от
1 мин частоту вращения от  300 об/мин до
300 об/мин до  180 об/мин. Момент инерции колеса
180 об/мин. Момент инерции колеса  2 кг·м2 . Найти угловое ускорение
2 кг·м2 . Найти угловое ускорение 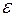 колеса, момент сил торможения и число оборотов
колеса, момент сил торможения и число оборотов 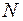 , за время
, за время 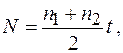
 4 об/с=240 об/мин.
4 об/с=240 об/мин.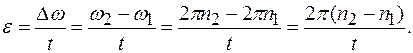
 2·3,14(3-5)/60 рад/с=-0,21 рад/с.
2·3,14(3-5)/60 рад/с=-0,21 рад/с. , вычисляя, находим:
, вычисляя, находим:  0,42 Н·м.
0,42 Н·м. . Чему равна его кинетическая энергия? Покажите на рисунке векторы скорости и ускорения для некоторых точек, лежащих на ободе диска.
. Чему равна его кинетическая энергия? Покажите на рисунке векторы скорости и ускорения для некоторых точек, лежащих на ободе диска. .
.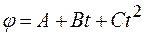 , где А=2 рад, В=32 рад/с, С= -4 рад/с2. Найти среднюю мощность
, где А=2 рад, В=32 рад/с, С= -4 рад/с2. Найти среднюю мощность  , развиваемую силами, действующими на маховик при его вращении, до остановки, если его момент инерции J=100 кг·м2.
, развиваемую силами, действующими на маховик при его вращении, до остановки, если его момент инерции J=100 кг·м2. 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения.
0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения.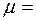 0,05.
0,05.