|
|
РЕКОМЕНДАЦИИ ПО РЕШЕНИЮ ЗАДАЧ
Предложить единую схему решения задач невозможно, однако можно рекомендовать определенную последовательность действий. Приступая к решению задач по какому-либо разделу, необходимо ознакомиться с конкретными физическими понятиями и соотношениями этого раздела, разобрать приведенные примеры решения задач. При самостоятельном решении задач целесообразно придерживаться следующей схемы: 1) по условию задачи представьте себе физическое явление, о котором идет речь, сделайте краткую запись условия, выразив исходные данные в единицах СИ; 2) сделайте, если это необходимо, рисунок, поясняющий описываемый в задаче процесс; 3) напишите уравнение или систему уравнений, отображающих физический процесс; 4) преобразуйте уравнения так, чтобы в них входили лишь исходные данные и табличные величины; 5) решите задачу в общем виде; 6) произведите вычисления и оцените реальность числового ответа.
Примеры решения задач Пример 1. Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид x=A+Bt+Ct3, где A=4 м, B=2 м/с, С=-0,5 м/с2. Для момента времени t1=2 с определить: 1) координату x1 точки, 2) мгновенную скорость v1, 3) мгновенное ускорение a1. Решение. 1. Координату точки, для которой известно кинематическое уравнение движения, найдем, подставив в уравнение движения вместо t заданное значение времени t1:
x=A+Bt+Ct3.
Подставим в это выражение значения A, В, С, t1 и произведем вычисления:
x=(4+4- 0,5 23) м=4 м.
2. Мгновенную скорость в произвольный момент времени найдем, продифференцировав координату х по времени:
Тогда в заданный момент времени t1 мгновенная скорость v1=B+3Ct12. Подставим сюда значения В, С, t1 и произведем вычисления: v1=-4 м/с. Знак минус указывает на то, что в момент времени t1=2 с точка движется в отрицательном направлении координатной оси. 3. Мгновенное ускорение в произвольный момент времени найдем, взяв вторую производную от координаты х по времени:
Мгновенное ускорение в заданный момент времени t1 равно a1=6Ct1. Подставим значения С, t1и произведем вычисления: a1=(-6 0,5 2) м/с=-6 м/с. Знак минус указывает на то, что направление вектора ускорения совпадает с отрицательным направлением координатной оси, причем в условиях данной задачи это имеет место для любого момента времени.
Пример 2. При падении тела с большой высоты его скорость vуст при установившемся движении достигает 80 м/с. Определить время τ, в течение которого начиная от момента начала падения скорость становится равной 1/2 vуст. Силу сопротивления воздуха принять пропорциональной скорости тела. Решение. На падающее тело действуют две силы: сила тяжести Сила сопротивления воздуха по условиям задачи пропорциональна скорости тела и противоположна ей по направлению:
где k - коэффициент пропорциональности, зависящий от размеров, формы тела и от свойств окружающей среды. Напишем уравнение движения тела в соответствии со вторым законом Ньютона в векторной форме:
Подставив выражение для
Спроецируем все векторные величины на вертикально направленную ось и напишем уравнение для проекций:
После разделения переменных получим
Выполним интегрирование, учитывая, что при изменении времени от нуля до τ (искомое время) скорость возрастает от нуля до 1/2vуст
После интегрирования получаем
Подставим пределы интегрирования в левую часть равенства:
и найдем из полученного выражения искомое время:
Входящий сюда коэффициент пропорциональности k определим из следующих соображений. При установившемся движении (скорость постоянна) алгебраическая сумма проекций (на ось y) сил, действующих на тело, равна нулю, т. е. mg—kvуст=0, откуда k=mg/vуст. Подставим найденное значение k в полученную формулу для τ:
После сокращений и упрощений получим
Подставив в эту формулу значения vуст, g, ln2 и произведя вычисления, получим τ=5,66 с.
Пример 3. Два шара массами m1=2,5 кг и m2=1,5 кг движутся навстречу друг другу со скоростями v1=6 м/с и v2=2 м/с. Определить: 1) скорость и шаров после удара; 2) кинетические энергии шаров W1 до и W2 после удара; 3) долю кинетической энергии w шаров, превратившейся во внутреннюю энергию. Удар считать прямым, неупругим. Решение. 1. Неупругие шары не восстанавливают после удара своей первоначальной формы. Следовательно, не возникают силы, отталкивающие шары друг от друга, и шары после удара будут двигаться совместно с одной и той же скоростью и. Определим эту скорость по закону сохранения импульса. Так как шары движутся вдоль одной прямой, то этот закон можно записать в скалярной форме:
откуда
Направление скорости первого шара примем за положительное; тогда при вычислении скорость второго шара, который движется навстречу первому, следует взять со знаком минус:
u=(2,5 6—1,5 2)/(2,5+1,5) м/с=3 м/с.
2. Кинетические энергии шаров до и после удара определим по формулам
Произведя вычисления по этим формулам, получим
W1=(2,5 62/2+1,5 22/2)=48 (Дж); W2=(2,5+1,5) 32 =18 (Дж).
3. Сравнение кинетических энергий шаров до и после удара показывает, что в результате неупругого удара шаров произошло уменьшение их кинетической энергии, за счет чего увеличилась их внутренняя энергия. Долю кинетической энергии шаров, пошедшей на увеличение их внутренней энергии, определим из соотношения
Пример 4. Платформа в виде диска радиусом R= 1,5 м и массой m1=180 кг вращается по инерции около вертикальной оси с частотой n=10 мин-1. В центре платформы стоит человек массой т2=60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы? Решение. По закону сохранения момента импульса,
где J1 - момент инерции платформы; J2 - момент инерции человека, стоящего в центре платформы; Линейная скорость человека, стоящего на краю платформы, связана с угловой скоростью соотношением
Определив отсюда ω' и подставив полученное выражение в формулу закона сохранения момента импульса, будем иметь
v=(J1+J2)ω R/(J1+J'2)
Момент инерции платформы рассчитываем как для диска; следовательно, Заменив в формуле скорости величины J1, J2, J'2. и ω их выражениями, получим
Сделав подстановку значений т1, т2, п, R и π, найдем линейную скорость человека:
Пример 5.Кинетическая энергия WK электрона равна 1 МэВ. Определить скорость электрона. Решение. Релятивистская формула кинетической энергии
где E0=m0c2 - энергия покоя электрона. Выполнив относительно β преобразования, найдем скорость частицы, выраженную в долях скорости света (β=v/c):
Вычисления по этой формуле можно производить в любых единицах энергии, так как наименования единиц в правой части формул сократятся, и в результате подсчета будет получено отвлеченное число. Подставив числовые значения Е0и WK в мегаэлектрон-вольтах, получим β=0,941. Так как v=βc, то v =0,941∙3∙108= 2,82·108 (м/с). Чтобы определить, является ли частица с кинетической энергией WK релятивистской или классической, достаточно сравнить кинетическую энергию частицы с ее энергией покоя. Если
Пример 6.Материальная точка массой т=5 г совершает гармонические колебания с периодом Т=2 с. Амплитуда колебаний A=3 см. Определить: 1) скорость v точки в момент времени, когда смещение х=1,5 см; 2) максимальную силу Fmax, действующую на точку. Решение. 1. Уравнение гармонического колебания имеет вид
а формулу скорости получим, взяв первую производную по времени от смещения:
Чтобы выразить скорость через смещение, надо исключить из формул время. Для этого возведем оба уравнения в квадрат, разделим первое на А2, второе на A2ω 2 и сложим:
Решив последнее уравнение относительно v , найдем
Поскольку
Выполнив вычисления, получим Знак плюс соответствует случаю, когда направление скорости совпадает с положительным направлением оси х, знак минус – случаю, когда направление скорости совпадает с отрицательным направлением оси х. 2. Силу, действующую на точку, найдем по второму закону Ньютона:
где а - ускорение точки, которое получим, взяв производную по времени от скорости:
Подставив выражение ускорения в формулу второго закона Ньютона, получим
Отсюда максимальное значение силы
Подставив в это уравнение значения величин π, T, т и A, найдем
Пример 7.Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых Решение. Чтобы найти уравнение траектории точки, исключим время t из заданных уравнений. Для этого воспользуемся формулой
В данном случае α=ωt, поэтому
Как следует из условия задачи,
Полученное выражение представляет собой уравнение параболы, ось которой совпадает с осью Ох. Из уравнений, заданных в условии задачи, следует, что смещение точки по осям координат ограничено и заключено в пределах от -1 до +1 см по оси Ох и от -2 до +2 см по оси Оу.
Пример 8. Найти молярную массу М смеси кислорода массой m1=25 г и азота массой m2=75 г. Решение. Молярная масса смеси Мсм есть отношение массы смеси тсм к количеству вещества смеси υсм т.е.
Mсм=mсм/υсм
Масса смеси равна сумме масс компонентов смеси mсм=m1+m2. Количество вещества смеси равно сумме количеств вещества компонентов. Подставив в формулу (1) выражения mсм и υсм, получим
Молярные массы M1 кислорода и М2, азота:M1 =32×10-3 кг/моль, М2=28×10-3 кг/моль. Подставим значения величин и произведем вычисления:
Пример 9. В баллоне объемом V=10 л находится гелий под давлением p1=l МПа при температуре T1=300 К. После того как из баллона был израсходован гелий массой m=10 г, температура в баллоне понизилась до T2=290 К. Определить давление p2 гелия, оставшегося в баллоне. Решение. Для решения задачи воспользуемся уравнением Клапейрона - Менделеева, применив его дважды к начальному и конечному состояниям газа. Для начального состояния уравнение имеет вид
p1V=
а для конечного состояния –
p2V=
где m1 и m2 - массы гелия в начальном и конечном состояниях. Выразим массы m1 и m2 гелия:
и вычтем m2 из m1:
Отсюда найдем искомое давление:
Подставив значения величин, получим р2=3,64∙105 Па Пример 10. Найти среднюю кинетическую энергию одной молекулы аммиака NH3 при температуре t=27°С и среднюю энергию вращательного движения этой молекулы при той же температуре. Решение. Средняя полная энергия молекулы определяется по формуле
где i - число степеней свободы молекулы; k - постоянная Больцмана; Т - термодинамическая температура газа: T=t+Т0, где Т0=273 К. Число степеней свободы i четырехатомной молекулы, какой является молекула аммиака, равно 6. Подставив значения величин, получаем
Средняя энергия вращательного движения молекулы определяется по формуле
где число 3 означает число степеней свободы поступательного движения. Подставим значения величин и вычислим:
Пример 11. Средняя длина свободного пробега <l> молекулы углекислого газа при нормальных условиях равна 40 нм. Определить среднюю арифметическую скорость <v> молекул и число z соударений, которые испытывает молекула в 1 с. Решение. Средняя арифметическая скорость молекул определяется по формуле
где М - молярная масса вещества. Подставив числовые значения, получим <v>=362 м/с. Среднее число z соударений молекулы в 1 с определяется отношением средней скорости <v> молекулы к средней длине ее свободного пробега <l>:
Подставив в эту формулу значения <v>=362 м/с, <l>=40 нм=4×10-8 м, получим z= 9,05×109 с-1.
Пример 12. Определить изменение DS энтропии при изотермическом расширении кислорода массой m=10 г от объема V1=25 л до объема V2=100 л. Решение. Так как процесс изотермический, то в общем выражении энтропии температуру выносят за знак интеграла. Выполнив это, получим
Количество теплоты Q, полученное газом, найдем по первому началу термодинамики: Q=DU+A. Для изотермического процесса DU=0, следовательно, Q=A, а работа А для этого процесса определяется по формуле
С учетом этого получаем
Подставив числовые значения и произведя вычисления, получим
DS=(10×10-3/(32×10-3)) ×8,31 ln(100×10-3/(25×10-3))=3,60 (Дж/К).
ЗАДАЧИ
1. Три четверти своего пути автомобиль прошел со скоростью v1=60 км/ч, остальную часть пути - со скоростью v2=80 км/ч. Какова средняя путевая скорость <v> автомобиля? 2. Первую половину пути тело двигалось со скоростью v1=2 м/с, вторую - со скоростью v2=8 м/с. Определить среднюю путевую скорость <v> . 3.Движение материальной точки задано уравнением x=At+Bt2, где A=4 м/с, В= - 0,05 м/с2. Определить момент времени, в который скорость v точки равна нулю. Найти координату и ускорение в этот момент. 4. Движения двух материальных точек выражаются уравнениями:x1=A1+B1t+C1t2, x2=A2+B2t+C2t2, где A1=20 м, A2=2 м, B1=B2=2 м/с, C1= - 4 м/с2, С2=0,5 м/с2. В какой момент времени t скорости этих точек будут одинаковыми? Определить скорости v1 и v2 и ускорения a1 и а2 точек в этот момент. 5. Две материальные точки движутся согласно уравнениям: x1=A1t+B1t2+C1t3, x2=A2t+B2t2+C2t3, где A1=4 м/c, B1=8 м/с2, C1=- 16 м/с3, A2=2 м/с, B2= - 4 м/с2, С2=1м/с3. В какой момент времени t ускорения этих точек будут одинаковы? Найти скорости v1 и v2 точек в этот момент. 6.Камень брошен вертикально вверх с начальной скоростью v0=20 м/с. Через какое время камень будет находиться на высоте h=15м? Найти скорость v камня на этой высоте. Сопротивлением воздуха пренебречь. Принять g=10 м/с2. 7. Вертикально вверх с начальной скоростью v0=20 м/с брошен камень. Через τ=1 с после этого брошен вертикально вверх другой камень с такой же скоростью. На какой высоте h встретятся камни? 8.Движение точки по прямой задано уравнением x=At+Bt2, где A =2 м/с, В= - 0,5 м/с2. Определить среднюю путевую скорость <v> движения точки в интервале времени от t1=l с до t2=3 с. 9. Точка движется по прямой согласно уравнению x=At+Bt3, где A=6 м/с, В= - 0,125 м/с3. Определить среднюю путевую скорость <v> точки в интервале времени от t1=2 с до t2=6 с. 10. Тело, брошенное вертикально вверх, находилось на одной и той же высоте h=8,6 м два раза с интервалом Dt=3 с. Пренебрегая сопротивлением воздуха, вычислить начальную скорость брошенного тела. 11.Движение материальной точки задано уравнением 12.Движение точки по окружности радиусом R=4 м задано уравнением S=A+Bt+Ct2, где A=10 м, В=-2 м/с, С=1 м/с2. Найти тангенциальное а 13. По дуге окружности радиусом R=10 м движется точка. В некоторый момент времени нормальное ускорение точки аn=4,9 м/с2; в этот момент векторы полного и нормального ускорений образуют угол φ=60°. Найти скорость v и тангенциальное ускорение a 14. Точка движется по окружности радиусом R=2 м согласно уравнению S=At3, где A=2 м/с3. В какой момент времени t нормальное ускорение аn точки будет равно тангенциальному а 15. Движение точки по кривой задано уравнениями x=A1t3 и y=A2t, где A1=l м/с3, A2=2 м/с. Найти уравнение траектории точки, ее скорость v и полное ускорение а в момент времени t=0,8 с. 16.Камень брошен с вышки в горизонтальном направлении с начальной скоростью v0=30 м/с. Определить скорость v, тангенциальное a 17.Диск радиусом R=20 см вращается согласно уравнению φ=A+Bt+Сt3, где A=3 рад, В=-1 рад/с, С=0,1 рад/с3. Определить тангенциальное a 18. Колесо автомашины вращается равноускоренно. Сделав N=50 полных оборотов, оно изменило частоту вращения от n1=4 с1 до n2=6 с1. Определить угловое ускорение e и время вращения Δt колеса. 19. Диск вращается с угловым ускорением ε= - 2 рад/с2. Сколько оборотов N сделает диск при изменении частоты вращения от n1=240 мин-1 до n2=90 мин-1? Найти время Δt, в течение которого это произойдет. 20. Автомобиль движется по закруглению шоссе, имеющему радиус кривизны R=50 м. Уравнение движения автомобиля имеет вид S(t)=A+Bt+Ct2, где A=10 м, B=10 м/с, С=-0,5 м/с2. Найти скорость v автомобиля, его тангенциальное aτ, нормальное аn. и полное а ускорения в момент времени t=5 с. 21. Два бруска массами m1=l кг и m2=4 кг, соединенные шнуром, лежат на столе. С каким ускорением а будут двигаться бруски, если к одному из них приложить силу F=10 H, направленную горизонтально? Какова будет сила натяжения Т шнура, соединяющего бруски, если силу F=10 Н приложить к первому бруску? ко второму бруску? Трением пренебречь. 22. Наклонная плоскость, образующая угол α=25° с плоскостью горизонта, имеет длину l=2 м. Тело, двигаясь равноускоренно, соскользнуло с этой плоскости за время t=2 с. Определить коэффициент трения μ тела о плоскость. 23. Материальная точка массой т=2 кг движется под действием некоторой силы F согласно уравнению x=A+Bt+Ct2+Dt3, где С=1 м/с2, D=-0,2 м/с3. Найти значения этой силы в моменты времени t1=2 с и t2=5 с. В какой момент времени сила равна нулю? 24. Шарик массой m=300 г ударился о стену и отскочил от нее. Определить импульс p1, полученный стеной, если в последний момент перед ударом шарик имел скорость v0=10 м/с, направленную под углом α=30° к поверхности стены. Удар считать абсолютно упругим. 25. Автоцистерна с керосином движется с ускорением а=0,7 м/с2. Под каким углом α к плоскости горизонта расположен уровень керосина в цистерне? 26. Бак в тендере паровоза имеет длину l=4 м. Какова разность Δl уровней воды у переднего и заднего концов бака при движении поезда с ускорением a=0,5 м/с2? 27. Катер массой m=2 т с двигателем мощностью N=50 кВт развивает максимальную скорость vmах =25 м/с. Определить время τ, в течение которого катер после выключения двигателя потеряет половину своей скорости. Принять, что сила сопротивления движению катера изменяется пропорционально квадрату скорости. 28. Снаряд массой т=10 кг выпущен из зенитного орудия вертикально вверх со скоростью v0=800 м/с. Считая силу сопротивления воздуха пропорциональной скорости, определить время t подъема снаряда до высшей точки. Коэффициент сопротивления k=0,25 кг/с. 29. С вертолета, неподвижно висящего на некоторой высоте над поверхностью Земли, сброшен груз массой m=100 кг. Считая, что сила сопротивления воздуха изменяется пропорционально скорости, определить, через какой промежуток времени Δt ускорение а груза будет равно половине ускорения свободного падения. Коэффициент сопротивления k=10 кг/с. 30. Моторная лодка массой m=400 кг начинает двигаться по озеру. Сила тяги F мотора равна 0,2 кН. Считая силу сопротивления Fc пропорциональной скорости, определить скорость v лодки через Δt=20 с после начала ее движения. Коэффициент сопротивления k=20 кг/с. 31. На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса человека М =60 кг, масса доски т=20 кг. С какой скоростью и (относительно пола) будет двигаться тележка, если человек пойдет вдоль доски со скоростью (относительно доски) v=1 м/с? Массой колес пренебречь. Трение во втулках не учитывать. 32. В лодке массой m1=240 кг стоит человек массой m2=60 кг. Лодка плывет со скоростью v1=2 м/с. Человек прыгает с лодки в горизонтальном направлении со скоростью v=4 м/с (относительно лодки). Найти скорость и движения лодки после прыжка человека в двух случаях: 1) человек прыгает вперед по движению лодки и 2) в сторону, противоположную движению лодки. 33. Диск радиусом R=40 см вращается вокруг вертикальной оси. На краю диска лежит кубик. Принимая коэффициент трения μ=0,4, найти частоту п вращения, при которой кубик соскользнет с диска. 34. Автомобиль идет по закруглению шоссе, радиус R кривизны которого равен 200 м. Коэффициент трения μ колес о покрытие дороги равен 0,1 (гололед). При какой скорости v автомобиля начнется его занос? 35. Материальная точка массой m=2 кг двигалась под действием некоторой силы, направленной вдоль оси Ох согласно уравнению x=A+Bt+Ct2+Dt3, где В= - 2 м/с, С=1 м/с2, D= - 0,2 м/с3. Найти мощность N, развиваемую силой в момент времени t1=2 с и t2=5 с. 36. Мотоциклист едет по горизонтальной дороге. Какую наименьшую скорость v он должен развить, чтобы, выключив мотор, проехать по треку, имеющему форму «мертвой петли» радиусом R=4 м? Трением и сопротивлением воздуха пренебречь. 37. Конькобежец, стоя на льду, бросил вперед гирю массой m1=5 кг и вследствие отдачи покатился назадсо скоростью v2=1 м/с. Масса конькобежца m2=60 кг. Определить работу A, совершенную конькобежцем при бросании гири. 38. Два неупругих шара массами m1=2 кг и m2=3 кг движутся со скоростями соответственно v1=8 м/с и v1=4 м/с. Определить увеличение DU внутренней энергии шаров при их столкновении в двух случаях: 1) меньший шар нагоняет больший; 2) шары движутся навстречу друг другу. 39. Шар массой m1, летящий со скоростью v1=5 м/с, ударяет неподвижный шар массой m2. Удар прямой, неупругий. Определить скорость и шаров после удара, а также долю ω кинетической энергии летящего шара, израсходованной на увеличение внутренней энергии этих шаров. Рассмотреть два случая: 1) т1=2 кг, m2=8 кг; 2) m1=8 кг, m2=2 кг. 40. Шар массой m1=200 г, движущийся со скоростью v1=10 м/с, ударяет неподвижный шар массой m2=800 г. Удар прямой, абсолютно упругий. Каковы будут скорости v1 и v2 шаров после удара? 41. Вычислить момент инерции J проволочного прямоугольника со сторонами а=12 см и b=16 см относительно оси, лежащей в плоскости прямоугольника и проходящей через середины малых сторон. Масса равномерно распределена по длине проволоки с линейной плотностью τ=0,1 кг/м. 42. Определить момент инерции J кольца массой т=50 г и радиусом R=10 см относительно оси, лежащей в плоскости кольца и касательной к нему. 43. Диаметр диска d=20 см, масса т=800 г. Определить момент инерции J диска относительно оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. 44. Найти момент инерции J плоской однородной прямоугольной пластины массой т=800 г относительно оси, совпадающей с одной из ее сторон, если длина а другой стороны равна 40 см. 45. Определить момент инерции J тонкой плоской пластины со сторонами а=10 см и b=20 см относительно оси, проходящей через центр масс пластины параллельно большей стороне. Масса пластины равномерно распределена по ее площади с поверхностной плотностью σ=1,2 кг/м2. 46.Тонкий однородный стержень длиной l=50 см и массой m=400 г вращается с угловым ускорением ε=3 рад/с2 около оси, проходящей перпендикулярно стержню через его середину. Определить вращающий момент М. 47.Вал массой m=100 кг и радиусом R=5см вращался с частотой n=8 с-1. К цилиндрической поверхности вала прижали тормозную колодку с силой F=40 H, под действием которой вал остановился через t=10 с. Определить коэффициент трения μ. 48.Через блок, имеющий форму диска, перекинут шнур. К концам шнура привязали грузики массой m1=100 г и т2=110 г. С каким ускорением а будут двигаться грузики, если масса т блока равна 400 г? Трение при вращении блока ничтожно мало. 49. Шар массой m=10 кг и радиусом R=20 см вращается вокруг оси, проходящей через его центр. Уравнение вращения шара имеет вид φ=A+Bt2+Ct3, где В=4 рад/с2, С= - 1 рад/с3. Найти закон изменения момента сил, действующих на шар. Определить момент сил М в момент времени t=2с. 50. Через неподвижный блок массой т=0,2 кг перекинут шнур, к концам которого подвесили грузы массами m1=0,3кг и m2=0,5 кг. Определить силы натяжения T1 и T2 шнура по обе стороны блока во время движения грузов, если масса блока равномерно распределена по ободу. 51. Человек стоит на скамье Жуковского и ловит рукой мяч массой m=0,4 кг, летящий в горизонтальном направлении со скоростью v=20 м/с. Траектория мяча проходит на расстоянии r =0,8 м от вертикальной оси вращения скамьи. С какой угловой скоростью w начнет вращаться скамья Жуковского с человеком, поймавшим мяч, если суммарный момент инерции J человека и скамьи равен 6 кг·м2? 52.Шарик массой т=100 г, привязанный к концу нити длиной l1=l м, вращается, опираясь на горизонтальную плоскость, с частотой n1=1 с-1. Нить укорачивается и шарик приближается к оси вращения до расстояния l2=0,5 м. С какой частотой n2 будет при этом вращаться шарик? Какую работу А совершит внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь. 53.Маховик вращается по закону, выраженному уравнением φ=A+Bt+Ct2, где A=2 рад, B=32 рад/с, С= - 4 рад/с2. Найти среднюю мощность <N>, развиваемую силами, действующими на маховик при его вращении, до остановки, если его момент инерции J=100 кг·м2. 54.Маховик в виде диска массой m=80 кг и радиусом R=30см находится в состоянии покоя. Какую работу A1нужно совершить, чтобы сообщить маховику частоту n=10 с-1? Какую работу A2 пришлось бы совершить, если бы при той же массе диск имел меньшую толщину, но вдвое больший радиус? 55.Маховик, момент инерции J которого равен 40 кг·м2, начал вращаться равноускоренно из состояния покоя под действием момента силы М=20 Н·м. Вращение продолжалось в течение t=10 с. Определить кинетическую энергию, приобретенную маховиком. 56. Обруч и сплошной цилиндр, имеющие одинаковую массу т=2 кг, катятся без скольжения с одинаковой скоростью v=5 м/с. Найти кинетические энергии W1 и W2 этих тел. 57.Шар катится без скольжения по горизонтальной поверхности. Полная кинетическая энергия Т шара равна 14 Дж. Определить кинетическую энергию поступательного и вращательного движения шара. 58.Определить линейную скорость v центра шара, скатившегося без скольжения с наклонной плоскости высотой h=1м. 59.Сколько времени t будет скатываться без скольжения обруч с наклонной плоскости длиной l=2 м и высотой h=10 см? 60.Тонкий прямой стержень длиной l=1м прикреплен к горизонтальной оси, проходящей через его конец. Стержень отклонили на угол φ=60° от положения равновесия и отпустили. Определить линейную скорость v нижнего конца стержня в момент прохождения через положение равновесия. 61. Фотонная ракета движется относительно Земли со скоростью v=0,6 с. Во сколько раз замедлится ход времени в ракете с точки зрения земного наблюдателя? 62. Собственное время жизни τ0 мю-мезона равно 2 мкс. От точки рождения до точки распада в лабораторной системе отсчета мю-мезон пролетел расстояние l=6 км. С какой скоростью v (в долях скорости света) двигался мезон? 63.Две релятивистские частицы движутся в лабораторной системе отсчета со скоростями v1=0,6 с и v2=0,9 с вдоль одной прямой. Определить их относительную скорость u21 в двух случаях: 1) частицы движутся в одном направлении; 2) частицы движутся в противоположных направлениях. |
|
 .
.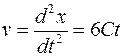 .
.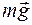 и сила сопротивления воздуха
и сила сопротивления воздуха  .
. ,
, .
. , получим
, получим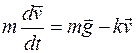 .
.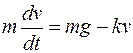
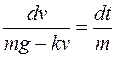
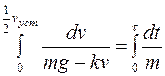
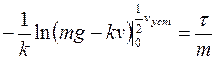


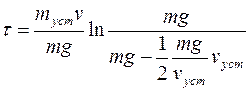

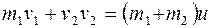 ,
,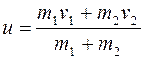 .
.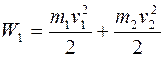 ;
; 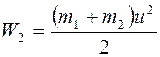 .
. ;
; 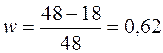 .
.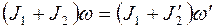 ,
, - угловая скорость платформы с человеком, стоящим в ее центре; J2' - момент инерции человека, стоящего на краю платформы; ω' - угловая скорость платформы с человеком, стоящим на ее краю.
- угловая скорость платформы с человеком, стоящим в ее центре; J2' - момент инерции человека, стоящего на краю платформы; ω' - угловая скорость платформы с человеком, стоящим на ее краю.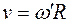 .
.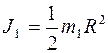 . Момент инерции человека рассчитываем как для материальной точки. Поэтому J2=0, J'2=m2R2. Угловая скорость платформы до перехода человека равна ω=2πn.
. Момент инерции человека рассчитываем как для материальной точки. Поэтому J2=0, J'2=m2R2. Угловая скорость платформы до перехода человека равна ω=2πn.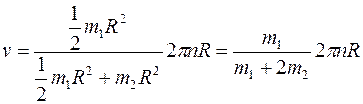
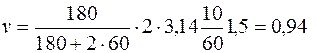 (м/с).
(м/с).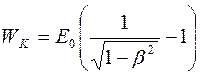
 .
. <<1, частицу можно считать классической.
<<1, частицу можно считать классической.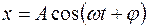

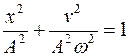

 , получаем
, получаем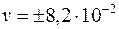 м/c
м/c



 Н.
Н. ,
,  , где А1=1 см, A2=2 см, ω=π с-1. Найти уравнение траектории точки.
, где А1=1 см, A2=2 см, ω=π с-1. Найти уравнение траектории точки.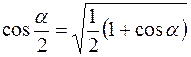
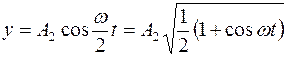
 , и уравнение траектории
, и уравнение траектории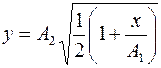 .
.
 (кг/моль)
(кг/моль) RT1,
RT1, RT2,
RT2, ;
; 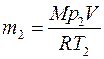
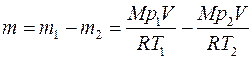
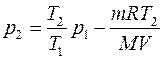

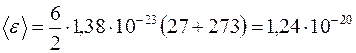 Дж.
Дж.
 Дж.
Дж.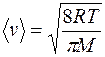
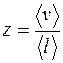 .
.
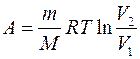
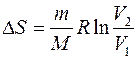
 , где A=10 м, В= - 5 м/с2, С=10 м/с. Найти выражения для скорости
, где A=10 м, В= - 5 м/с2, С=10 м/с. Найти выражения для скорости  и ускорения
и ускорения  . Для момента времени t=1с вычислить: 1) модуль скорости
. Для момента времени t=1с вычислить: 1) модуль скорости 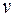 ; 2) модуль ускорения
; 2) модуль ускорения  ; 3) модуль тангенциального ускорения
; 3) модуль тангенциального ускорения  ; 4)модуль нормального ускорения
; 4)модуль нормального ускорения  .
.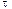 , нормальное an и полное а ускорения точки в момент времени t=2с.
, нормальное an и полное а ускорения точки в момент времени t=2с. ?Определить полное ускорение а в этот момент.
?Определить полное ускорение а в этот момент. и нормальное an ускорения камня в конце второй секунды после начала движения.
и нормальное an ускорения камня в конце второй секунды после начала движения. нормальное аn и полное а ускорения точек на окружности диска для момента времени t=10 с.
нормальное аn и полное а ускорения точек на окружности диска для момента времени t=10 с.