|
|
Приклади розв’язування задачПрактичне заняття № 10 Тема: Використання законів заломлення План: 1. Плоскопаралельна пластинка. 2. Призма. 3. Збираюча та розсіююча лінзи. 4. Хід променів у цих приладах. Формули. 5. Практичне призначення цих приладів.
Основні формули: 1) 2) 3) 4) 5) Приклади розв’язування задач Задача № 1 Визначити, наскільки плоскопаралельна скляна пластинка зміщує у сторону промінь світла, який падає на неї під кутом Аналіз та розв’язок Дано:
Величину зміщення x знаходимо з Підставляємо:
Відповідь:
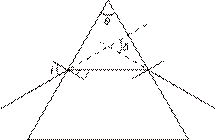
Задача № 2 Призма із заломлюючим кутом Аналіз та розв’язок Дано:
Запишемо формулу призми для кута найменшого відхилення для першого та другого випадків: Скорочуємо і одержимо Знайдемо Обчислимо Відповідь:
Задача № 3 Відстань від лампочки до екрану Аналіз та розв’язок Дано:
Запишемо формулу лінзи для першого та другого випадків:
Прирівняємо: Відповідь:
Задачі для самостійного розв'язування та домашнього завдання: 10.1. В яких межах може змінюватись кут відхилення променя при проходженні крізь скляну призму ( 10.2. Промінь світла падає на грань скляної призми під прямим кутом і виходить з протилежної грані, відхилившись від попереднього напрямку на кут 10.3. Який заломлюючий кут у скляної призми, якщо кут найменьшого відхилення проміня в ній дорівнює цьому заломлюючому кутові? 10.4. На грань скляної призми із заломлюючим кутом 10.5. Заломлюючий кут призми, яка має форму гострого клина, 10.6 Чому дорівнює кут найменьшого відхилення для лінії 10.7. Промінь світла падає під кутом 10.8. На плоскопаралельну скляну пластинку товщиною 1 см падає промінь світла під кутом 10.9. У воді йдуть два паралельних промені 1 і 2. Промінь 1 виходить у повітря безпосередньо, а промінь 2 проходить крізь горизонтальну плоскопаралельну скляну пластинку. а) Чи будуть промені 1 і 2 паралельні при виході в повітря? б) Чи вийде в повітря промінь 2, якщо промінь 1 зазнає повне внутрішнє відбивання (див. рисунок)?
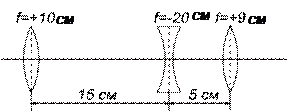
10.10. Промінь світла проходить крізь декілька прозорих плоскопаралельних пластин. При кожному заломленні втрачається 0,1 частина сили світла; всередині кожної пластини поглинається 0,2 сили світла. Яка сила світла, що пройшло крізь 5 пластин, якщо початкова сила світла дорівнює 10 св? 10.11. При розгляді предмета крізь призму найбільша чіткість виходить при найменшому відхиленні променів. Чому? 10.12. а) який заломлюючий кут у скляній призмі, якщо кут найменшого відхилення дорівнює заломлюючому куту? б) який повинен бути коефіцієнт заломлення середовища, з якого зроблена призма, щоб умова а) могла бути виконана? 10.13. Маємо дві однакові призми з заломлюючими кутами 10.14. Намалювати, як ідуть у призмі з приломлюючим кутом 10.15. Лінза з фокусною відстанню 10.16. Знайти фокусну відстань 10.17. Лінза з показником заломлення 1,53 занурена у сірковуглець 10.18. За допомогою тонкої збиральної скляної лінзи з показником заломлення 1,5 одержано дійсне зображення предмета на відстані 10 см від лінзи. Після того, як предмет і лінзу розташували у воді, не змінюючи відстані між ними, зображення одержано на відстані 60 см від лінзи. Знайти фокусну відстань 10.19. Зображення предмета, яке знаходилось на відстані 10 см від тонкої лінзи, пряме та збільшене у 2 рази. Визначити фокусну відстань лінзии 10.20. На систему лінз, зображених на рисунку, падає зліва паралельний пучок світла. Знайти положення точки сходження цього пучка після проходження системи.
10.21. Вивести формулу тонкої лінзи в формі Ньютона: 10.22. Знайти головну фокусну відстань наступних лінз: 10.23. Радіуси викривлення поверхней двоякоопуклої лінзи дорівнюють 10.24. Лінза з фокусною відстанню 16 см дає різке зображення предмета при двох положеннях, відстань між якими 60 см. Знайти відстань від предмета до екрана. 10.25. Знайти продольну хроматичну аберацію двоякоопуклої лінзи з флінтгласу з однаковими радіусами викривлення 10.26. Шляхом побудування знайти побічний фокус двоякоопуклої лінзи для похилого паралельного пучка світла, який падає на лінзу ( 10.27. Знайти точку перетинання променя з оптичною віссю. Див. рисунок.
Практичне заняття № 11 Тема: Оптичні прилади. План: 1.Лупа. 2.Мікроскоп. 3.Телескопічна система. 4.Фотоапарат, проекційний апарат, дзеркала. Основні формули: 1) 2) 3) 4) 5) Для різних випадків 6) Приклади розв’язування задач Задача № 1 Фокусна відстань об'єктива мікроскопа дорівнює
Дано:
З урахуванням знаків запишемо формулу лінзи для окуляру
Відповідь:
Задача № 2 Телескоп, об’єктив якого має діаметр Аналіз та розв’язок
В телескопі задній фокус об’єктива співпадає з переднім фокусом окуляра. Оскільки розглядається віддалена точка, то можна вважати, що на об’єктив падає паралельний пучок променів, і з окуляра виходить теж паралельний пучок. З рисунка видно, що Відповідь:
Задача № 3 Необхідно виготовити фотографічним шляхом шкалу, розділену на деякі долі міліметра. Фокусна відстань об’єктива 13,5 см. На якій відстані від об’єктива треба помістити шкалу, щоб вона була зменшена в 10 разів? Аналіз та розв’язок: Для рішення задачі намалюємо хід променів у фотоапараті. Щоб отримати зменшене зображення, необхідно помістити предмет за подвійною фокусною відстанню об’єктива. Дано:
k =10
З умови задачі Запишемо формулу лінзи для цього випадку:
Відповідь: шкалу потрібно розмістити на відстані 148,5 см, тобто далеко за подвійною фокусною відстанню об’єктива.
Задача № 4 Два дзеркала нахилені один до одного і створюють двогранний кут Аналіз та розв’язок
Відповідь: дійсно, кут Задачі для самостійного розв'язування та домашнього завдання: 11.1. Мікроскоп складається з об’єктива з фокусною відстанню 2 мм та окуляра з фокусною відстанню 40 мм. Відстань між фокусами об’єктива та окуляра дорівнює 18 см. Знайти збільшення, яке дає мікроскоп. 11.2. Фокусна відстань об’єктива мікроскопа 11.3. Фокусна відстань одного з рефракторів у Пулкові 11.4. Фокусна відстань об’єктива проекційного ліхтаря дорівнює 0,25 м. Яке збільшення дає ліхтар, якщо екран знаходиться на відстані 2 м від об’єктива? 11.5. Знайти збільшення, яке дає лупа, фокусна відстань якої 2 см: 1)для нормального ока з відстанню найкращого зору в 25 см і 2) для короткозорого ока з відстанню найкращого зору в 15 см. 11.6. Фокусна відстань об’єктива телескопа 11.7. Зорова труба з фокусною відстанню об’єктива 11.8. Знайти збільшення зорової труби, кеплеровського типу, встановленної на нескінченність, коли 11.9. Трубу Кеплера, збільшення якої дорівнює 15, занурили у воду, яка заповнила і її внутрішню частину. Щоб система при тих же розмірах стала знову телескопічною, об’єктив замінили другим. Яке стало після цього збільшення труби у воді? Показник заломлення скла окуляра 11.10. Матове скло фотоапарата з фокусною відстанню 20 см встановлено так, що різким виходить предмет, який знаходиться на відстані 5 м. До якого діаметра 11.11. Хлопчик, знявши окуляри, читав книгу, яка знаходилась на відстані 16 см від очей. Якої оптичної сили у нього окуляри? Відповідь: -2,25 дп. 11.12. Діапозитив має розміри 11.13. Зорова труба відрегульована для спостереження Місяця. На яку відстань і в який бік треба передвинути окуляр, щоб можна було спостерігати предмети, розташовані від труби на 11.14. Оптичні сили об’єктива і окуляра мікроскопа дорівнюють відповідно 100 дп і 20 дп. Збільшення мікроскопа дорівнює 50. Яке буде збільшення цього мікроскопа, якщо відстань між об’єктивом і окуляром збільшити на 2 см? Відповідь: 60. 11.15. Коли оптична сила ока більше: при розгляді близьких чи далеких предметів? 11.16. У мікроскопах з великим збільшенням у простір між об’єктивом і покровним склом вводять кедрову олію, яка має показник заломлення такий самий, як і у покровного скла. Чому? 11.17. При якомусь розташуванні зображення предмета у вигнутому дзеркалі в три рази меньше самого предмета. Якщо ж предмет передвинути на відстань 11.18. Радіус викривлення вигнутого дзеркала 11.19. Два однакові вигнутих дзеркала розташовані один проти одного так, що їх головні фокуси співпадають. Світна точка Самостійна робота |
|
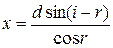 , де
, де 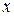 – величина зміщення променя,
– величина зміщення променя,  – кут падіння,
– кут падіння, 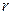 – кут заломлення,
– кут заломлення, 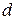 – товщина пластинки. Формула зміщення променя при падінні його на плоскопаралельну пластинку.
– товщина пластинки. Формула зміщення променя при падінні його на плоскопаралельну пластинку.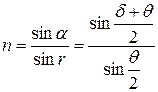 – формула призми для найменшого кута відхилення;
– формула призми для найменшого кута відхилення; 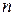 – показник заломлення призми,
– показник заломлення призми,  – кут найменшого відхилення,
– кут найменшого відхилення,  – заломлюючий кут призми.
– заломлюючий кут призми.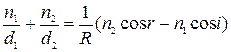 – основне рівняння оптичної техніки;
– основне рівняння оптичної техніки;  – показник заломлення першого середовища,
– показник заломлення першого середовища, 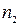 – показник заломлення другого середовища,
– показник заломлення другого середовища,  – відстань від точкового джерела світла до сферичної поверхні,
– відстань від точкового джерела світла до сферичної поверхні, 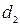 – відстань від поверхні до зображення цього джерела,
– відстань від поверхні до зображення цього джерела, 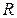 – радіус кривизни поверхні,
– радіус кривизни поверхні,  – формула лінзи.
– формула лінзи.  – рівняння Гауса з урахуванням правила знаків. У цих формулах:
– рівняння Гауса з урахуванням правила знаків. У цих формулах: 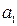 і
і  – спряжені відстані;
– спряжені відстані; 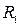 та
та  – радіуси кривизни поверхонь лінзи;
– радіуси кривизни поверхонь лінзи;  – фокусна відстань лінзи.
– фокусна відстань лінзи.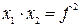 – рівняння Ньютона.
– рівняння Ньютона. 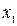 – відстань від предмета до переднього фокуса,
– відстань від предмета до переднього фокуса, 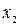 – відстань від зображення предмета до заднього фокуса.
– відстань від зображення предмета до заднього фокуса. . Товщина пластинки
. Товщина пластинки  см,
см, 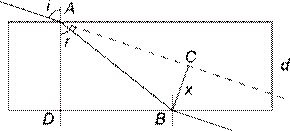

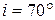
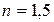

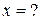
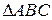 ;
;  , тобто
, тобто  .
.  знаходимо з
знаходимо з  :
:  .
.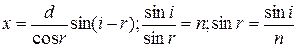 , тобто
, тобто  . Тоді
. Тоді  ;
;  см.
см. см. Зміщення тим більше, чим більше товщина пластинки, а також залежить від кута падіння променя на пластину.
см. Зміщення тим більше, чим більше товщина пластинки, а також залежить від кута падіння променя на пластину.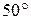 дає кут найменшого відхилення
дає кут найменшого відхилення  . Який кут найменшого відхилення одержимо, якщо цю призму покладемо у воду (показник заломлення – 1,33)?
. Який кут найменшого відхилення одержимо, якщо цю призму покладемо у воду (показник заломлення – 1,33)?
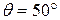
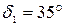

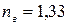
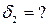
 ;
; 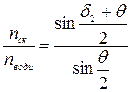 . Поділимо ліві та праві частини рівнянь, одержимо
. Поділимо ліві та праві частини рівнянь, одержимо 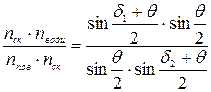 .
. .
.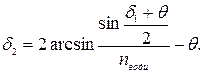
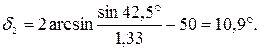
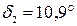 , тобто кут відхилення променя зменшується при зануренні призми у воду.
, тобто кут відхилення променя зменшується при зануренні призми у воду. см. Лінза, яка знаходиться між ними, дає чітке зображення лампи на екрані при двох положеннях, відстань між якими
см. Лінза, яка знаходиться між ними, дає чітке зображення лампи на екрані при двох положеннях, відстань між якими 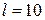 см. Знайти фокусну відстань лінзи.
см. Знайти фокусну відстань лінзи.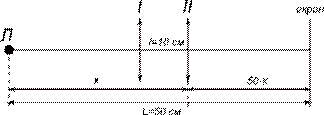


 та
та 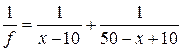 .
. ,
, 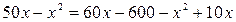 .
.  см. Підставимо в перше рівняння:
см. Підставимо в перше рівняння: 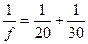 .
. 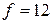 см.
см. см.
см.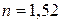 ), якщо її заломлюючий кут дорівнює
), якщо її заломлюючий кут дорівнює  ?
?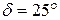 . Знайти заломлюючий кут призми.
. Знайти заломлюючий кут призми.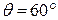 падає промінь світла під кутом
падає промінь світла під кутом  . Знайти кут заломлення проміня при виході із призми і кут відхилення проміня від початкового напрямку.
. Знайти кут заломлення проміня при виході із призми і кут відхилення проміня від початкового напрямку.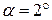 . Визначити кут найменьшого відхилення проміня, при проходженні крізь призму, якщо показник заломлення скла призми
. Визначити кут найменьшого відхилення проміня, при проходженні крізь призму, якщо показник заломлення скла призми  .
. натрію в призмі з заломлюючим кутом
натрію в призмі з заломлюючим кутом  на плоскопаралельну скляну пластинку і виходить із неї паралельно падаючому проміню. Показник заломлення скла 1,5. Яка товщина
на плоскопаралельну скляну пластинку і виходить із неї паралельно падаючому проміню. Показник заломлення скла 1,5. Яка товщина  між променями.
між променями.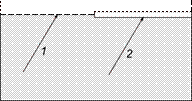
 і за нею два промені, які падають на призму паралельно стороні АВ. Чи змінюється відстань між променями? Чи однакові довжини першого та другого променів усередині скла?
і за нею два промені, які падають на призму паралельно стороні АВ. Чи змінюється відстань між променями? Чи однакові довжини першого та другого променів усередині скла? см зроблена зі скла з показником заломлення
см зроблена зі скла з показником заломлення  . Знайти фокусну відстань
. Знайти фокусну відстань 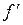 лінзи, яку розташовано у воді
лінзи, яку розташовано у воді 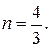
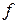 двояко-опуклої лінзи, яка обмежена сферичними поверхнями з радіусами
двояко-опуклої лінзи, яка обмежена сферичними поверхнями з радіусами  мм і
мм і 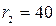 мм; показник заломлення скла лінзи
мм; показник заломлення скла лінзи  . Як зміниться фокусна відстань лінзи порівняно з фокусною відстанню її в повітрі?
. Як зміниться фокусна відстань лінзи порівняно з фокусною відстанню її в повітрі? .
.
 , де
, де 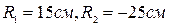 ;
;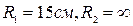 ;
; ;
;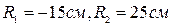 ;
; ;
;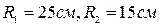 .
.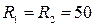 см. Показник заломлення матеріалу лінзи дорівнює 1,5. Знайти оптичну силу лінзи.
см. Показник заломлення матеріалу лінзи дорівнює 1,5. Знайти оптичну силу лінзи.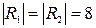 см. Показник заломлення флінтгласу для червоного та фіолетового променів дорівнюють відповідно 1,5 та 1,8 (
см. Показник заломлення флінтгласу для червоного та фіолетового променів дорівнюють відповідно 1,5 та 1,8 ( 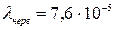 см,
см,  см).
см).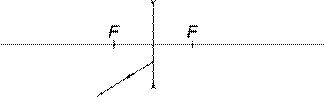
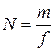 :
:  – збільшення лупи,
– збільшення лупи, 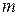 – відстань найкращого зору,
– відстань найкращого зору,  :
: 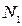 – збільшення об'єктиву,
– збільшення об'єктиву, 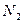 - збільшення окуляру.
- збільшення окуляру.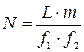 :
: 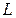 – оптичний інтервал,
– оптичний інтервал, 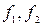 – фокусні відстані об'єктива і окуляра.
– фокусні відстані об'єктива і окуляра. – кутове збільшення телескопічної системи.
– кутове збільшення телескопічної системи. – формула дзеркала.
– формула дзеркала. 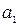 та
та 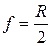 :
:  см, фокусна відстань окуляра
см, фокусна відстань окуляра  см. Відстань між ними дорівнює 20 см. На якій відстані повинен знаходитись об'єкт, щоб результуюче зображення було на відстані 20 см від ока. Яке при цьому буде лінійне збільшення мікроскопа?
см. Відстань між ними дорівнює 20 см. На якій відстані повинен знаходитись об'єкт, щоб результуюче зображення було на відстані 20 см від ока. Яке при цьому буде лінійне збільшення мікроскопа?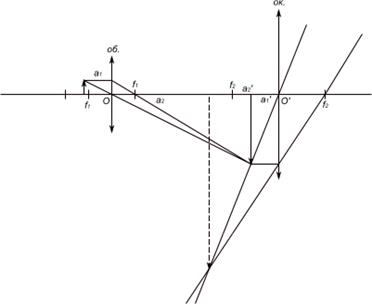 Аналіз та розв’язок
Аналіз та розв’язок

 см
см см
см
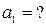
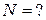
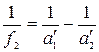 , звідки
, звідки 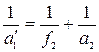 .
.  см. З рисунка видно, що
см. З рисунка видно, що  см.
см. 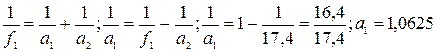 см.
см.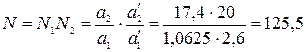 .
.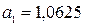 см,
см, 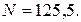
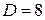 см, наведений на віддалену випромінюючу точку. З окуляра телескопа виходить паралельний пучок променів, який можливо спостерігати, якщо помістити перед окуляром матове скло, або лист папера як круглу світлу пляму. Діаметр цієї плями
см, наведений на віддалену випромінюючу точку. З окуляра телескопа виходить паралельний пучок променів, який можливо спостерігати, якщо помістити перед окуляром матове скло, або лист папера як круглу світлу пляму. Діаметр цієї плями  мм. Шлях проходження світла в телескопі не обмежений ніякими діафрагмами. Яке збільшення телескопа?
мм. Шлях проходження світла в телескопі не обмежений ніякими діафрагмами. Яке збільшення телескопа? Дано:
Дано:
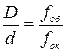 , а це якраз і є кутове збільшення телескопу
, а це якраз і є кутове збільшення телескопу  .
. . Основне в розв’язку цієї задачі – це правильно намальований рисунок.
. Основне в розв’язку цієї задачі – це правильно намальований рисунок.
 fоб =13,5
fоб =13,5 а1 - ?
а1 - ?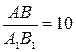 . Так як
. Так як  , то
, то  або
або 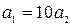 .
.
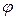 . На них падає промінь, розташований у площині, перпендикулярній до ребра кута. Показати, що кут
. На них падає промінь, розташований у площині, перпендикулярній до ребра кута. Показати, що кут  відхилення цього променя від початкового направлення після відбивання від обох дзеркал не залежить від кута падіння. Обчислити
відхилення цього променя від початкового направлення після відбивання від обох дзеркал не залежить від кута падіння. Обчислити 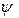 .
. Дано:
Дано:

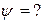
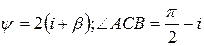 , тобто
, тобто 
 , тобто
, тобто 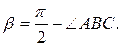
 , тому що
, тому що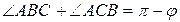 .
.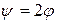 .
. , а відстань між об єктивом та окуляром 16 см, збільшення мікроскопа 200. Знайти збільшення окуляра.
, а відстань між об єктивом та окуляром 16 см, збільшення мікроскопа 200. Знайти збільшення окуляра.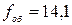 м. Яке збільшення цього рефрактора при користуванні окуляром з фокусною відстанню
м. Яке збільшення цього рефрактора при користуванні окуляром з фокусною відстанню  см?
см? см, його окуляр має фокусну відстань
см, його окуляр має фокусну відстань 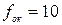 см. Діаметр повного місяця бачиться неозброєним оком під кутом
см. Діаметр повного місяця бачиться неозброєним оком під кутом 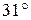 . Під яким кутом видно місяць у телескопі?
. Під яким кутом видно місяць у телескопі? см встановлена на нескінченність. На яку відстань
см встановлена на нескінченність. На яку відстань  треба передвинути окуляр труби, щоб ясно бачити предмети на відстані 50 м?
треба передвинути окуляр труби, щоб ясно бачити предмети на відстані 50 м? .
. .
. потрібно задіафрагмувати об’єктив, щоб не було помітної нерізкості у предметів, які знаходяться на 0,5 м ближче того, хто знімає, (нерізкість вважати непомітною, коли розмитість деталей не більше 0,1 мм)? Відповідь:
потрібно задіафрагмувати об’єктив, щоб не було помітної нерізкості у предметів, які знаходяться на 0,5 м ближче того, хто знімає, (нерізкість вважати непомітною, коли розмитість деталей не більше 0,1 мм)? Відповідь: 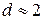 см.
см.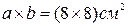 . Визначити оптичну силу тонкої збираючої лінзи, яка може служити об’єктивом проекційного апарата, якщо зображення діапозитива на екрані повинно мати розміри
. Визначити оптичну силу тонкої збираючої лінзи, яка може служити об’єктивом проекційного апарата, якщо зображення діапозитива на екрані повинно мати розміри  . Відстань від об єктива до екрана
. Відстань від об єктива до екрана 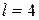 м. Відповідь:
м. Відповідь: 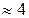 дп.
дп. м? Фокусна відстань об’єктива
м? Фокусна відстань об’єктива 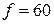 см. Відповідь:
см. Відповідь: 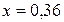 см.
см.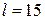 см ближче до дзеркала, то зображення стане в 1,5 рази менше предмета.Знайти фокусну відстань дзеркала. Відповідь:
см ближче до дзеркала, то зображення стане в 1,5 рази менше предмета.Знайти фокусну відстань дзеркала. Відповідь:  см. Знайти положення об'єкта, при якому його зображення буде дійсним і збільшеним у два рази. Знайти також положення, при якому зображення буде меншим та збільшеним у два рази. Побудувати зображення об'єкта в обох випадках. Відповідь: а)
см. Знайти положення об'єкта, при якому його зображення буде дійсним і збільшеним у два рази. Знайти також положення, при якому зображення буде меншим та збільшеним у два рази. Побудувати зображення об'єкта в обох випадках. Відповідь: а)  см, б)
см, б) 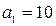 см.
см. розташована на загальній вісі дзеркал на відстані
розташована на загальній вісі дзеркал на відстані 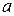 від першого дзеркала. Де буде зображення
від першого дзеркала. Де буде зображення 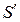 після відбивання від обох дзеркал? Відповідь: у тій же точці.
після відбивання від обох дзеркал? Відповідь: у тій же точці.