Занятие 2. Уравнение Шредингера. Краткие теоретические сведения
Основные понятия
Одномерное временное уравнение Шредингера
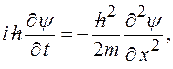
где  мнимая единица мнимая единица   масса частицы; масса частицы;  волновая функция, описывающая состояние частицы. волновая функция, описывающая состояние частицы.
Волновая функция, описывающая одномерное движение свободной частицы:

где  амплитуда волны де Бройля; амплитуда волны де Бройля;  импульс частицы; импульс частицы;  энергия частицы. энергия частицы.
Одномерное уравнение Шредингера для стационарных состояний:

где  полная энергия частицы; полная энергия частицы;  потенциальная энергия; потенциальная энергия;  координатная (или амплитудная) часть волновой функции. координатная (или амплитудная) часть волновой функции.
Для случая трех измерений  уравнение Шредингера записывается в виде: уравнение Шредингера записывается в виде:

или в операторной форме:

где  оператор Лапласа. оператор Лапласа.
Стандартные условия, которым должна удовлетворять волновая функция:
1) конечность (во всем пространстве; 2) однозначность; 3) непрерывность самой  функции и ее первой производной. функции и ее первой производной.
Вероятность  обнаружить частицу в интервале от обнаружить частицу в интервале от  до до  (в одномерном случае) выражается формулой: (в одномерном случае) выражается формулой:

где  плотность вероятности. плотность вероятности.
Вероятность  обнаружить частицу в интервале от обнаружить частицу в интервале от  до до  находится интегрированием находится интегрированием  в указанных пределах: в указанных пределах:

Собственное значение энергии  частицы, находящейся на частицы, находящейся на  м энергетическом уровне в бесконечно глубоком одномерном прямоугольном потенциальном ящике, определяется формулой: м энергетическом уровне в бесконечно глубоком одномерном прямоугольном потенциальном ящике, определяется формулой:

где  ширина потенциального ящика. ширина потенциального ящика.
Соответствующая этой энергии собственная волновая функция имеет вид:

Коэффициент преломления  волн де Бройля на границе низкого потенциального барьера бесконечной ширины (см Рис.1): волн де Бройля на границе низкого потенциального барьера бесконечной ширины (см Рис.1):

где  и и  длины волн де Бройля в областях I и II (частица движется из области I во II ); длины волн де Бройля в областях I и II (частица движется из области I во II );  соответствующие значения волновых чисел. соответствующие значения волновых чисел.
Коэффициенты отражения  и пропускания и пропускания 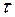 волн де Бройля через низкий волн де Бройля через низкий  потенциальный барьер бесконечной ширины: потенциальный барьер бесконечной ширины:
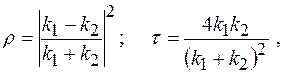
где  и и  волновые числа волн де Бройля в областях I и II. волновые числа волн де Бройля в областях I и II.
Коэффициент прозрачности  прямоугольного потенциального барьера конечной ширины: прямоугольного потенциального барьера конечной ширины:

где 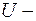 высота потенциального барьера; высота потенциального барьера;  энергия частицы; энергия частицы; 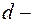 ширина барьера. ширина барьера.
Вопросы для ответа у доски
1. Каким свойствам должна удовлетворять волновая функция?
2. В чем заключается физический смысл волновой функции?
3. Для каких частиц справедливо уравнение Шредингера?
4. Почему уравнение Шредингера сформулировано как волновое уравнение?
5. Запишите временное и стационарное уравнение Шредингера и проанализируйте их.
6. Запишите одномерное временное и стационарное уравнения Шредингера и проанализируйте их.
Примеры решения задач:
Задача 1. Электрон находится в бесконечно глубоком одномерном прямоугольном потенциальном ящике шириной 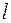 . Вычислить вероятность того, что электрон, находящийся в возбужденном состоянии ( . Вычислить вероятность того, что электрон, находящийся в возбужденном состоянии (  , будет обнаружен в средней трети ящика. , будет обнаружен в средней трети ящика.
Решение.
Вероятность  обнаружить частицу в интервале от обнаружить частицу в интервале от  : :

где  нормированная собственная волновая функция, отвечающая данному состоянию. нормированная собственная волновая функция, отвечающая данному состоянию.
Нормированная собственная волновая функция, описывающая состояние электрона в потенциальном ящике:

Возбужденному состоянию  отвечает собственная функция отвечает собственная функция 
Подставив  в подынтегральное выражение и вынеся постоянные величины за знак интеграла, получим: в подынтегральное выражение и вынеся постоянные величины за знак интеграла, получим:
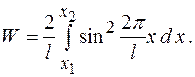 По условию По условию  и и  (см Рис.2). (см Рис.2).

Рис.2
Подставим пределы интегрирования, произведем замену
 . .
Получаем:

= 
По формулам приведения:

Подставив эти значения и произведя вычисления, получаем:

Ответ:. 
Задача 2. Моноэнергетический поток электронов  падает на низкий прямоугольный потенциальный барьер бесконечной ширины (см Рис.1). Определить высоту потенциального барьера падает на низкий прямоугольный потенциальный барьер бесконечной ширины (см Рис.1). Определить высоту потенциального барьера  , если известно, что 4% падающих на барьер электронов отражается. , если известно, что 4% падающих на барьер электронов отражается.
Решение.
Коэффициент отражения  от низкого потенциального барьера: от низкого потенциального барьера:

где  и и  волновые числа волн де Бройля в областях I и II (см Рис.1). волновые числа волн де Бройля в областях I и II (см Рис.1).
В области I кинетическая энергия электрона равна 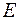 и волновое число: и волновое число:

Так как координата электрона не определена, то импульс электрона определяется точно и в данном случае можно говорить о точном значении кинетической энергии.
В области II кинетическая энергия электрона равна 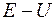 и волновое число: и волновое число:

В случае низкого потенциального барьера  действительны, а знак модуля можно опустить, тогда коэффициент отражения: действительны, а знак модуля можно опустить, тогда коэффициент отражения:

Разделим числитель и знаменатель дроби на  , ,
 . .
Решая уравнение относительно  , получаем: , получаем:

Возведя обе части равенства в квадрат, найдем высоту потенциального барьера:

Произведя вычисления, находим, что: U=55,6 эВ.
Ответ: 55,6 эВ.
Задача 3. Электрон с энергией Е =4,9 эВ движется в положительном направлении оси х (см Рис.3). Высота  потенциального барьера равна 5 эВ. При какой ширине потенциального барьера равна 5 эВ. При какой ширине  барьера вероятность барьера вероятность  прохождения электрона через него будет равна 0,2? прохождения электрона через него будет равна 0,2?
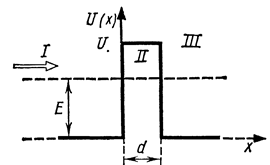
Решение.
Вероятность  прохождения частицы через потенциальный барьер по своему физическому смыслу совпадает с коэффициентом прозрачности прохождения частицы через потенциальный барьер по своему физическому смыслу совпадает с коэффициентом прозрачности  . Тогда вероятность того, что электрон пройдет через прямоугольный потенциальный барьер: . Тогда вероятность того, что электрон пройдет через прямоугольный потенциальный барьер:

где  масса электрона. Потенцируя, получаем: масса электрона. Потенцируя, получаем:
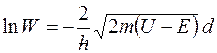 , отсюда . , отсюда . 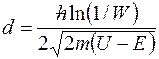 . .
Подставив числовые значения, находим:

Ответ: 
Задача 4. Найти энергию частицы 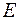 стационарного состояния массы стационарного состояния массы  в одномерной прямоугольной потенциальной яме шириной в одномерной прямоугольной потенциальной яме шириной 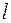 с абсолютно непроницаемыми стенками, если на границе ямы с абсолютно непроницаемыми стенками, если на границе ямы  известно значение производной известно значение производной  , т.е. , т.е.  . .
Решение.
Известно, что  функция функция  го стационарного состояния определяется по формуле: го стационарного состояния определяется по формуле:

Взяв ее производную по  и положив и положив  , получим: , получим:
 , отсюда , отсюда  . .
Подставив это значение в формулу для расчета энергии, получим:

Ответ: 
Задача 5. Частица массы  находится в двумерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками. Координаты находится в двумерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками. Координаты  и и  частицы находятся в интервалах соответственно частицы находятся в интервалах соответственно 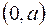 и и  , где , где  стороны ямы. Найти возможные значения энергии стороны ямы. Найти возможные значения энергии 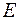 и нормированные и нормированные  функции частицы. функции частицы.
Решение.
В этом случае уравнение Шредингера имеет вид:
 (1) (1)
в пределах ямы 
На сторонах ямы  функция должна обращаться в нуль, поскольку является непрерывной (за пределами ямы функция должна обращаться в нуль, поскольку является непрерывной (за пределами ямы  ). Поэтому ). Поэтому  функцию внутри ямы удобнее искать в виде произведения синусов функцию внутри ямы удобнее искать в виде произведения синусов
 (2) (2)
так как на двух сторонах  автоматически автоматически  и и  равны нулю. равны нулю.
Возможные значения  найдем из условия обращения найдем из условия обращения  функции в нуль на противоположных сторонах ямы: функции в нуль на противоположных сторонах ямы:

 (3) (3)
После подстановки (3) в уравнение (2) получим  , и , и  в (1) получим: в (1) получим:
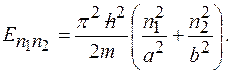 (4) (4)
Постоянную 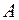 в (2) находим из условия нормировки в (2) находим из условия нормировки
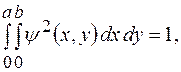
Откуда следует, что  Следовательно, нормированная Следовательно, нормированная  функция будет иметь вид: функция будет иметь вид:
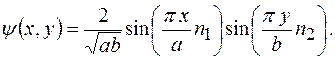
Ответ: 
Вопросы и задания для самопроверки
1. Каким свойствам должна удовлетворять волновая функция?
2. Записать уравнения Шредингера для стационарных состояний электрона, находящегося в атоме водорода.
3. Временная часть уравнения Шредингера имеет вид  Найти решение уравнения. Найти решение уравнения.
4. Что называется собственными значениями энергии и собственными функциями?
5. Какие состояния называются вырожденными? Что такое кратность вырождения?
6. В чем заключается физический смысл волновой функции?
7. Как рассчитать момент импульса и его проекцию на полярную ось в случае системы частиц?
8. Как обозначают и называют состояние электрона с разными орбитальными квантовыми числами?
9. Сопоставьте боровскую теорию атома водорода с квантово-механической теорией.
10. Как изменится коэффициент прозрачности потенциального барьера с увеличением его ширины в два раза?
11. Может ли частица находиться на дне «потенциальной ямы»? Определяется ли это формой «ямы»?
Задачи для самостоятельного решения
1. Частица в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной 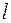 находится в возбужденном состоянии n=2. Определить, в каких точках интервала ( находится в возбужденном состоянии n=2. Определить, в каких точках интервала (  ) плотность вероятности нахождения частиц максимальна. ) плотность вероятности нахождения частиц максимальна.
2. Частица в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной 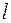 находится в возбужденном состоянии n =2. Найти вероятность нахождения частицы в последней трети ящика. находится в возбужденном состоянии n =2. Найти вероятность нахождения частицы в последней трети ящика.
3. Частица в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной 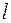 находится в основном состоянии. Найти вероятность нахождения частицы в области находится в основном состоянии. Найти вероятность нахождения частицы в области 
4. Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной 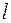 в основном состоянии. В каких точках интервала ( в основном состоянии. В каких точках интервала (  ) плотность вероятности нахождения частиц максимальна. ) плотность вероятности нахождения частиц максимальна.
5. Частица в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной 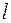 находится в возбужденном состоянии n =2. Определить, в каких точках интервала ( находится в возбужденном состоянии n =2. Определить, в каких точках интервала (  ) плотность вероятности нахождения частиц минимальна. ) плотность вероятности нахождения частиц минимальна.
6. Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной 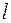 , в основном состоянии. Определить среднее значение координаты электрона. , в основном состоянии. Определить среднее значение координаты электрона.
7. Частица в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной 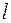 находится в возбужденном состоянии с n =2. Определить среднее значение координаты электрона. находится в возбужденном состоянии с n =2. Определить среднее значение координаты электрона.
8. Электрон находится в потенциальном ящике шириной 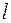 . В каких точках в интервале . В каких точках в интервале 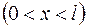 плотность вероятности нахождения электрона на первом и втором энергетических уровнях одинакова? Вычислить плотность вероятности для этих точек. Решение пояснить графически. плотность вероятности нахождения электрона на первом и втором энергетических уровнях одинакова? Вычислить плотность вероятности для этих точек. Решение пояснить графически.
9. Частица в потенциальном ящике находится в основном состоянии. Какова вероятность  нахождения частицы: 1) в средней трети ящика; 2) в крайней трети ящика? нахождения частицы: 1) в средней трети ящика; 2) в крайней трети ящика?
10. В одномерном потенциальном ящике шириной 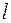 находится электрон. Вычислить вероятность находится электрон. Вычислить вероятность  нахождения электрона на первом энергетическом уровне в интервале нахождения электрона на первом энергетическом уровне в интервале  , равноудаленном от стенок ящика. , равноудаленном от стенок ящика.
11. Частица в потенциальном ящике шириной 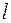 находится в низшем возбужденном состоянии. Определить вероятность находится в низшем возбужденном состоянии. Определить вероятность  нахождения частицы в интервале нахождения частицы в интервале  , равноудаленном от стенок ящика. , равноудаленном от стенок ящика.
12. Электрон находится в одномерной прямоугольной «потенциальной яму» шириной 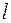 с бесконечно высокими «стенками». Определить вероятность с бесконечно высокими «стенками». Определить вероятность  обнаружения электрона в средней трети «ямы», если электрон находится в возбужденном состоянии ( обнаружения электрона в средней трети «ямы», если электрон находится в возбужденном состоянии (  2). Пояснить физический смысл полученного результата, изобразив графически плотность вероятности обнаружения электрона в данном состоянии. 2). Пояснить физический смысл полученного результата, изобразив графически плотность вероятности обнаружения электрона в данном состоянии.
13. Прямоугольный потенциальный барьер имеет ширину 0.1 нм. Определить в эВ разность энергий  при которой вероятность прохождения электрона сквозь барьер составит 0,99. при которой вероятность прохождения электрона сквозь барьер составит 0,99.
14. Вычислить отношение вероятностей  нахождения электрона на первом и втором энергетических уровнях в интервале нахождения электрона на первом и втором энергетических уровнях в интервале  , равноудаленном от стенок одномерной потенциальной ямы шириной , равноудаленном от стенок одномерной потенциальной ямы шириной 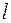 . .
15. Показать, что собственные функции  и и  описывающие состояние частицы в потенциальном ящике, удовлетворяют условию ортогональности, т.е. описывающие состояние частицы в потенциальном ящике, удовлетворяют условию ортогональности, т.е.
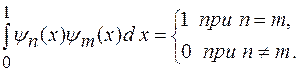
16. Используя выражение энергии  частицы, находящейся в потенциальном ящике, получить приближенное значение энергии: 1) гармонического осциллятора; 2) водородоподобного атома. Сравнить полученные результаты с истинными значениями энергий. частицы, находящейся в потенциальном ящике, получить приближенное значение энергии: 1) гармонического осциллятора; 2) водородоподобного атома. Сравнить полученные результаты с истинными значениями энергий.
17. Считая, что нуклоны в ядре находятся в трехмерном потенциальном ящике кубической формы с линейными размерами  10фм, оценить низший энергетический уровень нуклонов в ядре. 10фм, оценить низший энергетический уровень нуклонов в ядре.
18. Определить из условия нормировки коэффициент  собственной собственной  функции функции  описывающей состояние электрона в двумерном бесконечно глубоком потенциальном ящике со сторонами описывающей состояние электрона в двумерном бесконечно глубоком потенциальном ящике со сторонами  и и 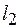 . .
19. Электрон находится в основном состоянии в двумерном квадратном бесконечно глубоком потенциальном ящике со сторонами 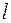 . Определить вероятность . Определить вероятность  нахождения электрона в области, ограниченной квадратом, который равноудален от стенок ящика и площадь которого составляет нахождения электрона в области, ограниченной квадратом, который равноудален от стенок ящика и площадь которого составляет  площади ящика. площади ящика.
20. Определить из условия нормировки коэффициент собственной  функции функции  описывающей состояние электрона в трехмерном потенциальном бесконечно глубоком ящике со сторонами описывающей состояние электрона в трехмерном потенциальном бесконечно глубоком ящике со сторонами 
21. Зная отношение амплитуд вероятности  для волны, отраженной от барьера, и для волны, отраженной от барьера, и  для проходящей волны, найти выражение для коэффициента отражения для проходящей волны, найти выражение для коэффициента отражения  и коэффициента прохождения и коэффициента прохождения 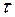 . .
22. Считая выражение для коэффициента отражения  от потенциального барьера и коэффициента прохождения от потенциального барьера и коэффициента прохождения 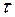 известными, показать, что известными, показать, что 
23. Протон с энергией  1 МэВ изменил при прохождении потенциального барьера дебройлевскую длину волны на 1% . Определить высоту 1 МэВ изменил при прохождении потенциального барьера дебройлевскую длину волны на 1% . Определить высоту  потенциального барьера. потенциального барьера.
24. На пути электрона с дебройлевской длиной волны 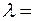 0,1 нм находится потенциальный барьер высотой 0,1 нм находится потенциальный барьер высотой  120 эВ. Определить длину волны де Бройля после прохождения барьера. 120 эВ. Определить длину волны де Бройля после прохождения барьера.
25. Определить показатель преломления  волн де Бройля при прохождении частицей потенциального барьера с коэффициентом отражения волн де Бройля при прохождении частицей потенциального барьера с коэффициентом отражения  0,5. 0,5.
26. Электрон с энергией  100 эВ попадает на потенциальный барьер высотой 100 эВ попадает на потенциальный барьер высотой  64 эВ. Определить вероятность 64 эВ. Определить вероятность  того, что электрон отразится от барьера. того, что электрон отразится от барьера.
27. Кинетическая энергия 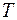 электрона в два раза превышает высоту электрона в два раза превышает высоту  потенциального барьера. Определить коэффициент отражения потенциального барьера. Определить коэффициент отражения  и коэффициент прохождения и коэффициент прохождения 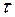 электронов на границе барьера. электронов на границе барьера.
28. Коэффициент прохождения 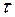 электронов через низкий барьер равен коэффициенту отражения электронов через низкий барьер равен коэффициенту отражения  . Определить во сколько раз кинетическая энергия . Определить во сколько раз кинетическая энергия 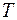 электронов больше высоты электронов больше высоты  потенциального барьера. потенциального барьера.
29. Коэффициент прохождения 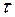 протонов через потенциальный барьер равен 0,8. Определить показатель преломления протонов через потенциальный барьер равен 0,8. Определить показатель преломления  волн де Бройля на границе барьера. волн де Бройля на границе барьера.
30. Вычислить коэффициент прохождения 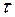 электрона с энергией электрона с энергией  100 эВ через потенциальный барьер высотой 100 эВ через потенциальный барьер высотой  99,75 эВ. 99,75 эВ.
|

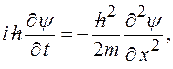
 мнимая единица
мнимая единица 
 масса частицы;
масса частицы;  волновая функция, описывающая состояние частицы.
волновая функция, описывающая состояние частицы.
 амплитуда волны де Бройля;
амплитуда волны де Бройля;  импульс частицы;
импульс частицы;  энергия частицы.
энергия частицы.
 потенциальная энергия;
потенциальная энергия;  координатная (или амплитудная) часть волновой функции.
координатная (или амплитудная) часть волновой функции. уравнение Шредингера записывается в виде:
уравнение Шредингера записывается в виде:

 оператор Лапласа.
оператор Лапласа. функции и ее первой производной.
функции и ее первой производной. обнаружить частицу в интервале от
обнаружить частицу в интервале от  до
до  (в одномерном случае) выражается формулой:
(в одномерном случае) выражается формулой:
 плотность вероятности.
плотность вероятности. обнаружить частицу в интервале от
обнаружить частицу в интервале от  до
до  находится интегрированием
находится интегрированием 
 частицы, находящейся на
частицы, находящейся на  м энергетическом уровне в бесконечно глубоком одномерном прямоугольном потенциальном ящике, определяется формулой:
м энергетическом уровне в бесконечно глубоком одномерном прямоугольном потенциальном ящике, определяется формулой:
 ширина потенциального ящика.
ширина потенциального ящика.
 волн де Бройля на границе низкого потенциального барьера бесконечной ширины (см Рис.1):
волн де Бройля на границе низкого потенциального барьера бесконечной ширины (см Рис.1):
 и
и  длины волн де Бройля в областях I и II (частица движется из области I во II );
длины волн де Бройля в областях I и II (частица движется из области I во II );  соответствующие значения волновых чисел.
соответствующие значения волновых чисел. и пропускания
и пропускания 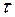 волн де Бройля через низкий
волн де Бройля через низкий  потенциальный барьер бесконечной ширины:
потенциальный барьер бесконечной ширины: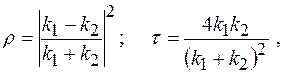
 и
и  волновые числа волн де Бройля в областях I и II.
волновые числа волн де Бройля в областях I и II. прямоугольного потенциального барьера конечной ширины:
прямоугольного потенциального барьера конечной ширины:
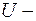 высота потенциального барьера;
высота потенциального барьера; 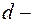 ширина барьера.
ширина барьера.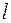 . Вычислить вероятность того, что электрон, находящийся в возбужденном состоянии (
. Вычислить вероятность того, что электрон, находящийся в возбужденном состоянии (  , будет обнаружен в средней трети ящика.
, будет обнаружен в средней трети ящика. :
:
 нормированная собственная волновая функция, отвечающая данному состоянию.
нормированная собственная волновая функция, отвечающая данному состоянию.

 в подынтегральное выражение и вынеся постоянные величины за знак интеграла, получим:
в подынтегральное выражение и вынеся постоянные величины за знак интеграла, получим: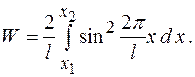 По условию
По условию  и
и  (см Рис.2).
(см Рис.2).
 .
.




 падает на низкий прямоугольный потенциальный барьер бесконечной ширины (см Рис.1). Определить высоту потенциального барьера
падает на низкий прямоугольный потенциальный барьер бесконечной ширины (см Рис.1). Определить высоту потенциального барьера  , если известно, что 4% падающих на барьер электронов отражается.
, если известно, что 4% падающих на барьер электронов отражается.
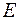 и волновое число:
и волновое число:
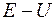 и волновое число:
и волновое число:
 действительны, а знак модуля можно опустить, тогда коэффициент отражения:
действительны, а знак модуля можно опустить, тогда коэффициент отражения:
 ,
, .
. , получаем:
, получаем:

 барьера вероятность
барьера вероятность 
 . Тогда вероятность того, что электрон пройдет через прямоугольный потенциальный барьер:
. Тогда вероятность того, что электрон пройдет через прямоугольный потенциальный барьер:
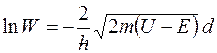 , отсюда .
, отсюда . 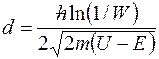 .
.

 в одномерной прямоугольной потенциальной яме шириной
в одномерной прямоугольной потенциальной яме шириной  известно значение производной
известно значение производной  , т.е.
, т.е.  .
.
 , получим:
, получим: , отсюда
, отсюда  .
.
 частицы находятся в интервалах соответственно
частицы находятся в интервалах соответственно 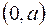 и
и  , где
, где  стороны ямы. Найти возможные значения энергии
стороны ямы. Найти возможные значения энергии  (1)
(1)
 ). Поэтому
). Поэтому  (2)
(2) автоматически
автоматически  и
и  равны нулю.
равны нулю. найдем из условия обращения
найдем из условия обращения 
 (3)
(3) , и
, и  в (1) получим:
в (1) получим: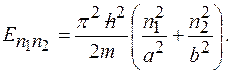 (4)
(4)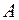 в (2) находим из условия нормировки
в (2) находим из условия нормировки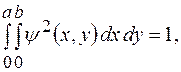
 Следовательно, нормированная
Следовательно, нормированная 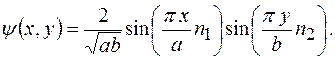

 Найти решение уравнения.
Найти решение уравнения. ) плотность вероятности нахождения частиц максимальна.
) плотность вероятности нахождения частиц максимальна.
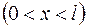 плотность вероятности нахождения электрона на первом и втором энергетических уровнях одинакова? Вычислить плотность вероятности для этих точек. Решение пояснить графически.
плотность вероятности нахождения электрона на первом и втором энергетических уровнях одинакова? Вычислить плотность вероятности для этих точек. Решение пояснить графически. , равноудаленном от стенок ящика.
, равноудаленном от стенок ящика. 2). Пояснить физический смысл полученного результата, изобразив графически плотность вероятности обнаружения электрона в данном состоянии.
2). Пояснить физический смысл полученного результата, изобразив графически плотность вероятности обнаружения электрона в данном состоянии. при которой вероятность прохождения электрона сквозь барьер составит 0,99.
при которой вероятность прохождения электрона сквозь барьер составит 0,99. нахождения электрона на первом и втором энергетических уровнях в интервале
нахождения электрона на первом и втором энергетических уровнях в интервале  и
и  описывающие состояние частицы в потенциальном ящике, удовлетворяют условию ортогональности, т.е.
описывающие состояние частицы в потенциальном ящике, удовлетворяют условию ортогональности, т.е.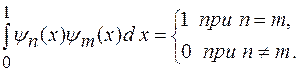
 частицы, находящейся в потенциальном ящике, получить приближенное значение энергии: 1) гармонического осциллятора; 2) водородоподобного атома. Сравнить полученные результаты с истинными значениями энергий.
частицы, находящейся в потенциальном ящике, получить приближенное значение энергии: 1) гармонического осциллятора; 2) водородоподобного атома. Сравнить полученные результаты с истинными значениями энергий. 10фм, оценить низший энергетический уровень нуклонов в ядре.
10фм, оценить низший энергетический уровень нуклонов в ядре. собственной
собственной  описывающей состояние электрона в двумерном бесконечно глубоком потенциальном ящике со сторонами
описывающей состояние электрона в двумерном бесконечно глубоком потенциальном ящике со сторонами  и
и 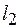 .
. описывающей состояние электрона в трехмерном потенциальном бесконечно глубоком ящике со сторонами
описывающей состояние электрона в трехмерном потенциальном бесконечно глубоком ящике со сторонами 
 для волны, отраженной от барьера, и
для волны, отраженной от барьера, и  для проходящей волны, найти выражение для коэффициента отражения
для проходящей волны, найти выражение для коэффициента отражения 
 1 МэВ изменил при прохождении потенциального барьера дебройлевскую длину волны на 1% . Определить высоту
1 МэВ изменил при прохождении потенциального барьера дебройлевскую длину волны на 1% . Определить высоту 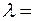 0,1 нм находится потенциальный барьер высотой
0,1 нм находится потенциальный барьер высотой  120 эВ. Определить длину волны де Бройля после прохождения барьера.
120 эВ. Определить длину волны де Бройля после прохождения барьера. 0,5.
0,5.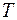 электрона в два раза превышает высоту
электрона в два раза превышает высоту