|
|
Формулировка транспортной задачиУЧЕБНОЕ ПОСОБИЕ для выполнения курсовых и расчетных работ по курсу «CALS-технологии»
Имитационные математические модели Транспортная задача Имитационное моделирование является мощным инструментом исследования сложных бизнес-процессов и систем и позволяет решать трудно формализуемые задачи в условиях неопределенности. При имитационном моделировании используемая математическая модель воспроизводит алгоритм («логику») функционирования исследуемой системы во времени при различных сочетаниях значений параметров системы и внешней среды. Поэтому данный метод позволяет совершенствовать системы поддержки принятия решений, улучшая, тем самым, экономические показатели организаций, уменьшая риск от реализации решений и экономя средства для достижения той или иной цели. Многие крупные компании (Xerox, Motorola, IBM, Intel, Ford) используют программы, предоставляющие возможность имитации принимаемых решений и исследования возможных изменений в экономической системе, возникающих в результате действия различных факторов, т.е. позволяющие выполнять проверку гипотезы «что будет, если…». В настоящее время успешная деятельность практически во всех сферах экономики не возможна без моделирования поведения и динамики развития процессов, изучения особенностей развития объектов, рассмотрения их функционирования в различных условиях. Имитационные модели позволяют проверить, правильно ли мы понимаем процессы в исследуемом объекте, и выявить в различных конкретных случаях параметры порядка. Знание последних и дает возможность строить простые модели сложных явлений. Имитационное моделирование подразделяется на несколько видов:
Агентное моделирование – относительно новое направление в имитационном моделировании, которое используется для исследования децентрализованных систем, динамика функционирования которых определяется не глобальными правилами и законами (как в других парадигмах моделирования), а наоборот, когда эти глобальные правила и законы являются результатом индивидуальной активности членов группы. Цель агентных моделей – получить представление об этих глобальных правилах, общем поведении системы, исходя из предположений об индивидуальном, частном поведении ее отдельных активных объектов и взаимодействии этих объектов в системе. Агент – некая сущность, обладающая активностью, автономным поведением, может принимать решения в соответствии с некоторым набором правил, взаимодействовать с окружением, а также самостоятельно изменяться. Дискретно-событийное моделирование – подход к моделированию, предлагающий абстрагироваться от непрерывной природы событий и рассматривать только основные события моделируемой системы, такие как: «ожидание», обработка заказа», «движение с грузом», «разгрузка» и другие. Дискретно-событийное моделирование наиболее развито и имеет огромную сферу приложений – от логистики и систем массового обслуживания до транспортных и производственных систем. Этот вид моделирования наиболее подходит для моделирования производственных процессов.
Стадии построения имитационной модели Построение имитационной модели сложной системы состоит из ряда взаимосвязанных стадий. 1. Составление модели на содержательном уровне – задача описывается на естественном языке и осуществляется ее системный анализ. 2. Разработка формализованной имитационной модели – модель остается имитационной, только содержательное описание заменяется формулами и элементами алгоритмов. 3. Составление программно-алгоритмической и информационной моделей, предназначенных для реализации имитационной модели на вычислительной технике с использованием языков программирования и моделирования, диалоговых средств общения, инструментальных и экспертных систем. Формулировка транспортной задачи Рассмотрим построение имитационной модели на примере решения транспортной задачи, т.е. определения минимальных затрат при производстве определенных материальных объектов или нахождение оптимальных путей для доставки грузов потребителю. Условие задачи. Пусть имеется m пунктов производства (отправления) груза A = {A1, A2, ... , Am} и и n пунктов потребления назначения (назначения) этого груза B = {B1, B2, ... , Bn}. В каждом пункте производства определены ресурсы груза ai (i=1,m), потребность в грузах в каждом пункте потребления bj (j=1,n) и заданы стоимости перемещения сij единицы груза из каждого i-го пункта производства в каждый j-й пункт потребления (рис. 1).
Рис.1. Постановка транспортной задачи в форме графа Требуется определить, какое количество груза xij необходимо перевезти из каждого i-го пункта отправления в каждый j-й пункт назначения, при выполнении следующих условий: 1. вывезти все грузы поставщиков; 2. удовлетворить потребности всех потребителей в грузах; 3. оптимизировать функцию приведенных затрат на перевозку грузов от поставщиков к потребителям.
Решение транспортной задачи Суммарные ресурсы в пунктах отправления и назначения равны соответственно a = Чтобы вывезти грузы всех поставщиков (условие 1), необходимо, чтобы выполнялось равенство a= Построение математической модели.Таким образом, задача линейного программирования сводится к транспортной задаче, которая в аналитической форме может быть представлена так: Функционал Y= Ограничения
В случае a 1. Если a > b, то вводится дополнительный фиктивный склад потребителя bn1=a–b и устанавливается стоимость перевозки ci,n1= 0, (i=1, m);
Целевая функция.Стоимость всех перевозок определяется как сумма произведений стоимости перевозок единицы товара на количество перевозимого по маршруту груза: Y = c11x11 + c12x12 + … + cijxij + … + cmnxmn, т.е. Y = Если перевозка по данному маршруту не определена, то xij=0. Критерием оптимизации являются минимальные затраты на доставку всего груза потребителю, т.е. Y® min. Задача сводится к нахождению таких xij, которые удовлетворяют ограничениям задачи и минимизируют суммарные затраты Y. В матричной форме данная задача представлена на рис. 2. В крайнем правом столбце и нижней строке матрицы записаны ресурсы соответствующих поставщиков и потребителей, а в клетках проставляется стоимость перевозки грузов.
Рис. 2. Представление транспортной задачи в матричной форме 12 |
|


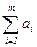 иb =
иb = 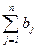 . Если общий объем производства (отправления) груза равен общему объему потребления (назначения), т.е. a = b, то такая задача называется сбалансированной (закрытой). В противном случае имеет место несбалансированная задача (открытая). Кроме того, в общем случае предполагается, что cij
. Если общий объем производства (отправления) груза равен общему объему потребления (назначения), т.е. a = b, то такая задача называется сбалансированной (закрытой). В противном случае имеет место несбалансированная задача (открытая). Кроме того, в общем случае предполагается, что cij 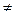 0.
0.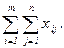 Чтобы удовлетворить заявки всех потребителей (условие 2), необходимо, чтобы выполнялось равенство b=
Чтобы удовлетворить заявки всех потребителей (условие 2), необходимо, чтобы выполнялось равенство b= 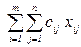 ®min.
®min.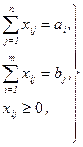
 2. Если a < b, то вводится дополнительный фиктивный склад поставщика am1=b–a и устанавливается стоимость перевозки cm1,j = 0, (j=1, n).
2. Если a < b, то вводится дополнительный фиктивный склад поставщика am1=b–a и устанавливается стоимость перевозки cm1,j = 0, (j=1, n).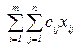 .
.