|
|
Регрессионные модели с переменной структурой(фиктивные переменные) До сих пор в качестве факторов рассматривались экономические переменные, принимающие количественные значения в некотором интервале. Вместе с тем может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровней. Это могут быть разного рода атрибутивные признаки, такие, например, как профессия, пол, образование, климатические условия, принадлежность к определенному региону. Чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, т.е. качественные переменные преобразованы в количественные. Такого вида сконструированные переменные в эконометрике принято называть фиктивными переменными. Рассмотрим применение фиктивных переменных для функции спроса. Предположим, что по группе лиц мужского и женского пола изучается линейная зависимость потребления кофе от цены. В общем виде для совокупности обследуемых уравнение регрессии имеет вид:
где Аналогичные уравнения могут быть найдены отдельно для лиц мужского пола: Различия в потреблении кофе проявятся в различии средних где
В общем уравнении регрессии зависимая переменная Для лиц мужского пола, когда Однако при введении двух фиктивных переменных
Предполагая при параметре
В рассматриваемой матрице существует линейная зависимость между первым, вторым и третьим столбцами: первый равен сумме второго и третьего столбцов. Поэтому матрица исходных факторов вырождена. Выходом из создавшегося затруднения может явиться переход к уравнениям
или
т.е. каждое уравнение включает только одну фиктивную переменную Предположим, что определено уравнение
где Теоретические значения размера потребления кофе для мужчин будут получены из уравнения
Для женщин соответствующие значения получим из уравнения
Сопоставляя эти результаты, видим, что различия в уровне потребления мужчин и женщин состоят в различии свободных членов данных уравнений: Теперь качественный фактор принимает только два состояния, которым соответствуют значения 1 и 0. Если же число градаций качественного признака-фактора превышает два, то в модель вводится несколько фиктивных переменных, число которых должно быть меньше числа качественных градаций. Только при соблюдении этого положения матрица исходных фиктивных переменных не будет линейно зависима и возможна оценка параметров модели. Пример. Проанализируем зависимость цены двухкомнатной квартиры от ее полезной площади. При этом в модель могут быть введены фиктивные переменные, отражающие тип дома: «хрущевка», панельный, кирпичный. При использовании трех категорий домов вводятся две фиктивные переменные: Предположим, что уравнение регрессии с фиктивными переменными составило:
Частные уравнения регрессии для отдельных типов домов, свидетельствуя о наиболее высоких ценах квартир в панельных домах, будут иметь следующий вид: «хрущевки» – Параметры при фиктивных переменных В отдельных случаях может оказаться необходимым введение двух и более групп фиктивных переменных, т.е. двух и более качественных факторов, каждый из которых может иметь несколько градаций. Например, при изучении потребления некоторого товара наряду с факторами, имеющими количественное выражение (цена, доход на одного члена семьи, цена на взаимозаменяемые товары и др.), учитываются и качественные факторы. С их помощью оцениваются различия в потреблении отдельных социальных групп населения, дифференциация в потреблении по полу, национальному составу и др. При построении такой модели из каждой группы фиктивных переменных следует исключить по одной переменной. Так, если модель будет включать три социальные группы, три возрастные категории и ряд экономических переменных, то она примет вид:
где
До сих пор мы рассматривали фиктивные переменные как факторы, которые используются в регрессионной модели наряду с количественными переменными. Вместе с тем возможна регрессия только на фиктивных переменных. Например, изучается дифференциация заработной платы рабочих высокой квалификации по регионам страны. Модель заработной платы может иметь вид:
где
………………………………………………………………………..
Поскольку последний район, указанный в модели, обозначен Мы рассмотрели модели с фиктивными переменными, в которых последние выступают факторами. Может возникнуть необходимость построить модель, в которой дихотомический признак, т.е. признак, который может принимать только два значения, играет роль результата. Подобного вида модели применяются, например, при обработке данных социологических опросов. В качестве зависимой переменной
Модель является вероятностной линейной моделью. В ней Среди моделей с фиктивными переменными наибольшими прогностическими возможностями обладают модели, в которых зависимая переменная |
|
 ,
,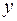 – количество потребляемого кофе;
– количество потребляемого кофе; 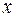 – цена.
– цена. и женского пола:
и женского пола:  .
. и
и  . Вместе с тем сила влияния
. Вместе с тем сила влияния 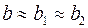 . В этом случае возможно построение общего уравнения регрессии с включением в него фактора «пол» в виде фиктивной переменной. Объединяя уравнения
. В этом случае возможно построение общего уравнения регрессии с включением в него фактора «пол» в виде фиктивной переменной. Объединяя уравнения 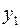 и
и  и, вводя фиктивные переменные, можно прийти к следующему выражению:
и, вводя фиктивные переменные, можно прийти к следующему выражению: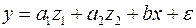 ,
, и
и  – фиктивные переменные, принимающие значения:
– фиктивные переменные, принимающие значения:

 . Переменная
. Переменная  рассматривается как дихотомическая переменная, принимающая всего два значения: 1 и 0. При этом когда
рассматривается как дихотомическая переменная, принимающая всего два значения: 1 и 0. При этом когда  , то
, то  , и наоборот.
, и наоборот.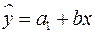 , а для лиц женского пола, когда
, а для лиц женского пола, когда  и
и  :
:  . Иными словами, различия в потреблении для лиц мужского и женского пола вызваны различиями свободных членов уравнения регрессии:
. Иными словами, различия в потреблении для лиц мужского и женского пола вызваны различиями свободных членов уравнения регрессии:  . Параметр
. Параметр  является общим для всей совокупности лиц, как для мужчин, так и для женщин.
является общим для всей совокупности лиц, как для мужчин, так и для женщин. и
и  приведет к вырожденной матрице исходных данных, а следовательно, и к невозможности получения их оценок. Объясняется это тем, что при использовании МНК в данном уравнении появляется свободный член, т.е. уравнение примет вид
приведет к вырожденной матрице исходных данных, а следовательно, и к невозможности получения их оценок. Объясняется это тем, что при использовании МНК в данном уравнении появляется свободный член, т.е. уравнение примет вид .
. независимую переменную, равную 1, имеем следующую матрицу исходных данных:
независимую переменную, равную 1, имеем следующую матрицу исходных данных: .
.
 ,
, .
. .
. – для мужчин.
– для мужчин. .
. ; панельные –
; панельные –  ; кирпичные –
; кирпичные –  .
. . Параметр при
. Параметр при  ,
,

 – экономические (количественные) переменные.
– экономические (количественные) переменные. ,
,


 , то в исследование включено
, то в исследование включено 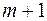 район.
район. .
.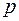 и
и  . Поэтому при решении модели находят оценку условной вероятности события
. Поэтому при решении модели находят оценку условной вероятности события  – характеристики альтернатив (время, цена),
– характеристики альтернатив (время, цена),  – характеристики индивидов (возраст, доход, уровень образования). Модель такого рода позволяет предсказать долю индивидов в генеральной совокупности, которые выбирают данную альтернативу.
– характеристики индивидов (возраст, доход, уровень образования). Модель такого рода позволяет предсказать долю индивидов в генеральной совокупности, которые выбирают данную альтернативу.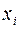 и фиктивных переменных
и фиктивных переменных