|
|
Теория вероятностей и математическая статистика
Основные теоретические сведения
1. Уравнение вида
2. Дифференциальное уравнение
3. Уравнение
4. Уравнение вида
где Если корни
Если
Если
5. Уравнение вида
называется неоднородным линейным уравнением второго порядка. Если Укажем правило нахождения частного решения Пусть 1) 2) 3) Пусть 1) 2) 6. Ряд вида
называется степенным рядом, При
7. Рядом Фурье периодической функции
Коэффициенты Фурье
Пример 1. Найти решение системы дифференциальных уравнений методом характеристического уравнения.
Решение. Частное решение системы будем находить в следующем виде
Составляем характеристическое уравнение и решаем его:
Корню
Полагаем
Корню
Получаем
Общее решение исходной системы имеет вид
Пример 2. Найти область сходимости степенного ряда Решение.Радиус сходимости степенного ряда определяется по формуле:
Так как
то
Степенной ряд сходится абсолютно в интервале Исследуем поведение ряда на концах интервала. При При ряда является полуинтервал Пример 3. Вычислить Решение. Разложение подынтегральной функции в степенной ряд имеет вид:
Интегрируя этот ряд почленно, получим
Полученный числовой ряд есть ряд Лейбница. Погрешность происходящая от отбрасывания всех членов начиная с третьего, будет по абсолютной величине меньше третьего члена:
Вычисляя с точностью до 0,0001, найдем
Пример 4. Разложить в ряд Фурье периодическую функцию, заданную на интервале – периоде.
Решение.Функция f(x) удовлетворяет условию Дирихле, поэтому раскладывается в ряд Фурье.
Вычисляя коэффициенты Фурье функции f(x):
так как
Контрольная работа №2 Задание 1.Найти неопределенные интегралы. Вариант 1. 1. 2. 3. Вариант 2. 1. 2. 3.
Вариант 3. 1. 2. 3. Вариант 4. 1. 2. 3. Вариант 5. 1. 2. 3. Вариант 6. 1. 2. 3. Вариант 7. 1. 2. 3. Вариант 8. 1. 2. 3. Вариант 9. 1. 2. 3. Вариант 10. 1. 2. 3.
Вариант 11. 1. 2. 3. Вариант 12. 1. 2. 3. Вариант 13. 1. 2. 3. Вариант 14. 1. 2. 3. Вариант 15. 1. 2. 3. Вариант 16. 1. 2. 3. Вариант 17. 1. 2. 3. Вариант 18. 1. 2. 3. Вариант 19. 1. 2. 3. Вариант 20. 1. 2. 3. Вариант 21. 1. 2. 3. Вариант 22. 1. 2. 3. Вариант 23. 1. 2. 3. Вариант 24. 1. 2. 3. Вариант 25. 1. 2. 3. Задание №2. Вычислить площадь фигуры, ограниченную заданными линиями. Вариант 1. Вариант 2. Вариант 3. Вариант 4. Вариант 5. Вариант 6. Вариант 7. Вариант 8. Вариант 9. Вариант 10. Вариант 11. Вариант 12. Вариант 13. Вариант 14. Вариант 15. Вариант 16. Вариант 17. Вариант 18. Вариант 19. Вариант 20. Вариант 21. Вариант 22. Вариант 23. Вариант 24. Вариант 25. Задание №3.Исследовать на сходимость ряд. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25.
Задание №4.Решить дифференциальное уравнение:
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25.
Задание №5.Найти все производные второго порядка следующих функций. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. Задание №6 Вычислить криволинейный интеграл 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. Задание №7Исследовать на экстремумы функцию 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25.
Задание №8.Вычислить двойной интеграл ограничена прямыми. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Гусак А.А. Высшая математика : в 2 т. / А.А. Гусак. Минск : ТетраСистемс, 1998. Т.1. 544 с. 2. Гусак А.А. Высшая математика : в 2 т. / А.А. Гусак. Минск : ТетраСистемс, 1998. Т.2. 448 с. 3. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. / В.А. Кудрявцев, Б.П. Демидович. М. : Наука, 1989. 656 с. 4. Пискунов Н.С. Дифференциальное и интегральное исчисления. в 2 т. М. : Наука, 1968. Т 1. 551 с. 5. Пискунов Н.С. Дифференциальное и интегральное исчисления. в 2 т. М. : Наука, 1968. Т 2. 312 с. 6. Шипачев В.С. Высшая математика. М. : Высш. шк., 1996. 480 с. 7. Сборник индивидуальных заданий по высшей математики : в 3ч. / А.П. Рябушко, В.В. Бархатов, В.В. Державец, И.Е. Юруть.. Минск : Высшэйш. шк., 1990. Ч. 1. 270 с. 8. Сборник индивидуальных заданий по высшей математики : в 3ч. / А.П. Рябушко, В.В. Бархатов, В.В. Державец, И.Е. Юруть. Минск: Высшэйш. шк. 1991. Ч. 2. 352 с. 9. Сборник индивидуальных заданий по высшей математики : в 3ч. / А.П. Рябушко, В.В. Бархатов, В.В. Державец, И.Е. Юруть. Минск: Высшэйш. шк. 1991. Ч. 3. 288 с. |
|
 называется дифференциальным уравнением с разделяющимися переменными. Его общим интегралом будет
называется дифференциальным уравнением с разделяющимися переменными. Его общим интегралом будет .
. называется однородным относительно переменных
называется однородным относительно переменных  и
и  , если
, если  – однородная функция нулевого измерения относительно своих аргументов, т.е.
– однородная функция нулевого измерения относительно своих аргументов, т.е.  . данное уравнение с помощью замены
. данное уравнение с помощью замены  сводится к уравнению с разделяющимися переменными.
сводится к уравнению с разделяющимися переменными. называется линейным дифференциальным уравнением. Общее решение уравнения находим по формуле
называется линейным дифференциальным уравнением. Общее решение уравнения находим по формуле .
. , (1)
, (1) и
и  – постоянные числа называется линейным однородным дифференциальным уравнением второго порядка. Квадратное уравнение
– постоянные числа называется линейным однородным дифференциальным уравнением второго порядка. Квадратное уравнение  называется характеристическим уравнением.
называется характеристическим уравнением. ,
,  характеристического уравнения действительны и различны, то общий интеграл уравнения (1) выражается формулой
характеристического уравнения действительны и различны, то общий интеграл уравнения (1) выражается формулой .
. , то общий интеграл уравнения (1) находится по формуле
, то общий интеграл уравнения (1) находится по формуле .
.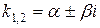 , то общее решение уравнения (1) находится по формуле
, то общее решение уравнения (1) находится по формуле .
. , (2)
, (2) – общее решение соответствующего однородного уравнения,
– общее решение соответствующего однородного уравнения,  – частное решение уравнения (2), то общее решение уравнения (2) имеет вид
– частное решение уравнения (2), то общее решение уравнения (2) имеет вид  .
. , тогда:
, тогда: , если
, если  не является корнем характеристического уравнения;
не является корнем характеристического уравнения; , если
, если 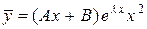 , если
, если  , тогда:
, тогда: , если число
, если число 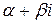 не является корнем характеристического уравнения;
не является корнем характеристического уравнения; , если число
, если число  (3)
(3)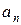 – коэффициенты ряда. Число
– коэффициенты ряда. Число  называется радиусом сходимости ряда, если ряд (3) сходится при
называется радиусом сходимости ряда, если ряд (3) сходится при  и расходится при
и расходится при  .
. ряд может как сходиться, так и расходиться. Интервал
ряд может как сходиться, так и расходиться. Интервал  называется интервалом сходимости ряда. Радиус сходимости
называется интервалом сходимости ряда. Радиус сходимости  .
. ,
, 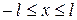 , называется ряд вида
, называется ряд вида .
. вычисляем по формулам
вычисляем по формулам  ,
,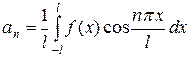 ,
,  .
.
 . Требуется определить постоянные К1, К2 и λ так, чтобы функции x(t), y(t) удовлетворяли заданной системе уравнений. Подставляя их в систему и сокращая на
. Требуется определить постоянные К1, К2 и λ так, чтобы функции x(t), y(t) удовлетворяли заданной системе уравнений. Подставляя их в систему и сокращая на 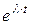 , получим систему уравнений:
, получим систему уравнений:

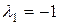 ,
,  – корни характеристического уравнения.
– корни характеристического уравнения. или
или  .
. , тогда
, тогда  . Получаем решение системы:
. Получаем решение системы: .
. или
или 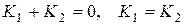 .
. . Получим решение системы:
. Получим решение системы: .
.
 .
.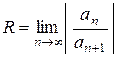 .
. ,
, .
. .
. имеем
имеем  , данный ряд расходится.
, данный ряд расходится. имеем
имеем  , ряд сходится по признаку Лейбница, причем сходится условно. Следовательно, область сходимости
, ряд сходится по признаку Лейбница, причем сходится условно. Следовательно, область сходимости .
. с точностью до
с точностью до  .
. .
.
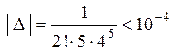 .
. .
.
 .
. ,
, ,
,
 ,
, .
. .
.

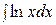




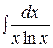






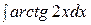






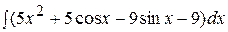
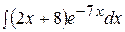

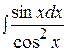

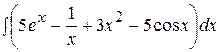











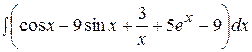









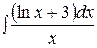


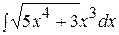








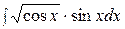



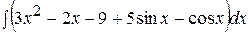


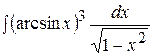

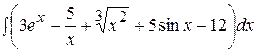

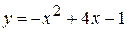 и
и 
 и
и 
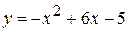 и
и 
 и
и 
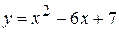 и
и 
 и
и 
 и
и 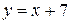


 и
и 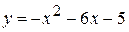 и
и  и
и 

 и
и 
 и
и 
 и
и 

 и
и 
 и
и  и
и 











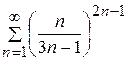






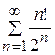



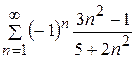

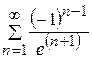


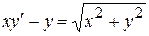







 .
.
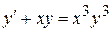







 .
.


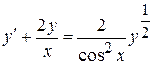











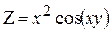





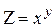





 , если:
, если: ,
,  ,
,  ,
, 
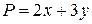 ,
, 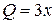 ,
,  ,
, 
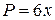 ,
,  ,
,  ,
,  ,
,  ,
, 
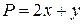 ,
,  ,
,  ,
, 
 ,
,  ,
, 
 ,
,  ,
,  ,
, 
 ,
,  ,
, 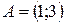 ,
, 
 ,
,  ,
,  ,
, 
 ,
,  ,
,  ,
, 
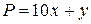 ,
,  ,
,  ,
, 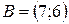
 ,
,  ,
,  ,
, 
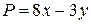 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 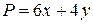 ,
,  ,
, 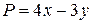 ,
, 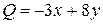 ,
,  ,
,  ,
, 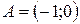 ,
,  ,
,  ,
,  ,
, 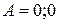 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
 , если:
, если:
























 , где область
, где область