Обратная связь
|
Теория вероятностей. Математическая статистика Предел
|
| ВОПРОС
|
| ОТВЕТ
| |
| Функция y = f(x) имеет пределом
|
| Функция y = f(x) имеет пределом число А при стремлении х к а, если для каждого числа е>0 найдется такое число δ>0, что
|y— A|<е, при | х —a|<δ
| |
| Математическая запись предела
|
| 
| |
| Предел постоянной величины
|
| limА=А
| |
| Предел суммы (разности) конечного числа функций
|
| 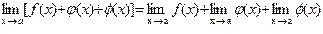
| |
| Предел частного двух функций
|
| 
| |
| Предел произведений конечного числа функций
|
|
 при lim φ(x)≠0
при lim φ(x)≠0
| |
| Чему равен замечательный предел:

|
|

| |
| Чему равен замечательный предел:

|
|

|
Производная. Применение производных для исследования функций
|
| ВОПРОС
|
| ОТВЕТ
| |
| Производной функции f(x)называется
|
| Производной функции f(x)называется предел отношения приращения функции Δу к приращению аргумента Δх в точке хпри стремлении Δх к нулю:
| |
| Математическая запись производной
|
| 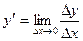
| |
| Производная
постоянной величины у=С:
|
|
ý=0;
| |
| Производная
степенной функции у = хμ:
|
|
ý=μxμ-1
| |
| Производная
показательной функции у = аx:
в частности, если у = ех
|
|
ý=axlna;
ý= еx;
| |
| Производная
логарифмической функции y=logax
|
| 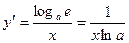 
| |
| Производная
натурального логарифма у = lnх
|
| 
| |
| Производная
тригонометрической функции y=sinx
|
| y'=cosx;
| |
| Производная
тригонометрической функции y=cos x
|
| ý =— sin x;
| |
| Производная тригонометрической функцииy = tgx
|
| 
| |
| Производная тригонометрической функцииy = ctgx
|
| 
| |
| Производная обратной тригонометрии-ческой функции y=arcsinx
|
| 
| |
| Производная обратной тригонометрии-ческой функции y=arccosx
|
| 
| |
| Производная обратной тригонометрии-ческой функции y=arctgx
|
| 
| |
| Производная обратной тригонометрии-ческой функции y=arcctgx
|
| 
| |
| Производная суммы (разности) функций y = w±u
|
| y' = u'±v'
| |
| Производная произведения двух функций y=uv
|
| y' = u'v + v'u.
| |
| Производная частного двух функций y=u/v
|
| 
| |
| Производная сложной функции
y = f1(u), если u = f2(x),
|
| у'x = у'ии'x
| |
| Условие возрастания функции y = f(x)на отрезке [а, b]
|
| f'(x)>0
| |
| Условие убывания функции y=f(x)на отрезке [а, b]
|
| f'(x)<0
| |
| Условие максимума функции y=f(x)при x= а
|
| f'(a)=0 и f'' (a)<0
| |
| Условия функции экстремума
|
| Если при х=а производные f'(а) = 0 и f"(а) = 0, то необходимо исследовать f'(x)в окрестностях точки x = а. Функция у=f(х)при х=а имеет максимум, если при переходе через точку х= а производная f'(x)меняет знак с «+» на «-», в случае минимума — с « - » на «+» Если f'(x)не меняет знака при переходе через точку х = а,то в этой точке у функции экстремума нет
|
Дифференциал функции. Применение
Дифференциала в приближенных вычислениях
|
| ВОПРОС
|
| ОТВЕТ
| |
| Дифференциал независимой переменной равен
|
| ее приращению: dx=Δx
| |
| Дифференциал функции y=f(x)
|
| dy = у' Δх
| |
| Дифференциал суммы (разности) двух функций y=u±v
|
| dy=du±dv
| |
| Дифференциал произведения двух функций у=uv
|
| dy = vdu+udv.
| |
| Дифференциал частного двух функций y=u/v
|
| 
| |
| Приращение функции через дифференциал
|
| Δy = f(x + Δx) - f(x) ≈ dy ≈ f'(x) • Δx
где Δx: — приращение аргумента
| |
| Приближенное вычисление значения функции:
|
| f(x + Δx) ≈ f(x) + f'(x) • Δx
| |
| Дифференциал применяется для вычисления абсолютной и относительной погрешностей при косвенных измерениях u = f(x, у, z .). Абсолютная погрешность результата измерения
|
|

| |
| Относительная погрешность результата измерения
|
|

|

Неопределенный интеграл
|
| ВОПРОС
|
| ОТВЕТ
| |
| первообразной данной функции f(x) называется
|
| Функция F(x),имеющая данную функцию f(x)своей производной или f(x)dxсвоим дифференциалом, называется первообразной данной функции f(x).
| |
| неопределенным интегралом называется
|
| Совокупность всех первообразных функций для дифференциала f(x)dxназывается неопределенным интегралом и обозначается символом ∫ f(x)dx.
| |
| Интеграл ∫xμdx равен
|
| xμ+1/ (μ+1) +C (μ≠-1)
| |
| Интеграл ∫dx/x равен
|
| ln|x|+C
| |
| Интеграл ∫axdx равен
|
| ax/lna +C
| |
| Интеграл ∫exdx равен
|
| ex+C
| |
| Интеграл ∫sin x dx равен
|
| -cos x +C
| |
| Интеграл ∫cos xdx равен
|
| sin x +C
| |
| Интеграл ∫dx/cos2x равен
|
| tgx+C
| |
| Интеграл ∫dx/sin2x равен
|
| -ctgx+C
| |
| Интеграл ∫dx равен
|
| х+С
| |
| Интеграл ∫arc sinxdx равен
|
| 
| |
| Интеграл ∫arc cosxdx равен
|
| - 
| |
| Интеграл ∫arc tgxdx равен
|
| 
| |
| Интеграл ∫arc ctgxdx равен
|
| - 
| |
| Интеграл ∫tgxdx равен
|
| Lncosx+C
| |
| Интеграл ∫ctgxdx равен
|
| - Lnsinx+C
| |
| Интегрирование по частям
|
| ∫ udv = uv—∫ vdu.
| |
| Найти у = ∫Ln хdх.
|
| Полагаем и=Lпх, dv = dx, тогда  ,
v = x
Используя формулу интегрирования по частям, получаем
у = ∫ Ln xdx = x Ln х-∫ dх = xLnx-x+C ,
v = x
Используя формулу интегрирования по частям, получаем
у = ∫ Ln xdx = x Ln х-∫ dх = xLnx-x+C
| |
| Интегрирование методом замены переменных Найти у= ∫ (1+ 2x2)dx
|
| Заменим l+2x=z,  Тогда
y=0,5∫z2dz Тогда
y=0,5∫z2dz
 Возвращаясь к прежней переменной х, окончательно имеем
Возвращаясь к прежней переменной х, окончательно имеем

|
Определенный интеграл
|
| ВОПРОС
|
| ОТВЕТ
| |
| Интегральная сумма
|
| ∑f(ki)Δxi ( от i=1 до n )
где ki — произвольная точка соответствующего отрезка
| |
| Определенный интеграл функции f(x) на отрезке [а, b]
|
| 
| |
| Формула Ньютона — Лейбница
|
|  где F′первообразная функцию f(x), т е
F′(x)=f(x)
где F′первообразная функцию f(x), т е
F′(x)=f(x)
| |
| свойства определенного интеграла

|
| 
| |
| свойства определенного интеграла
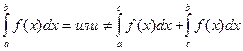
|
| 
| |
| свойства определенного интеграла

|
| 
| |
| Площадь криволинейной трапеции, ограниченной графиком функции f(x), осью абсцисс и прямыми х=а и х=b,
|
| 
| |
| Площадь фигуры, ограниченной двумя кривыми y=.f1(x)и у = f2(x) [ f'2(x)≥f1(x)]и двумя прямыми х=а и х=b,
|
| 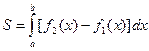
|
Дифференциальные уравнения
|
| ВОПРОС
|
| ОТВЕТ
| |
| Общий вид дифференциального уравнения
|
| F(x ,y,y′,y″,…yn) = О
| |
| Общee решение дифференциального уравнения
|
| y=f(x, C1,C2, , Сn)
| |
| Общий вид дифференциального уравнения первого порядка
|
| F(x,y,y') = 0
| |
| Общее решение дифференциального уравнения первого порядка
|
| y= f(x,C)
| |
| Дифференциальное уравнение типа y'=f(x)
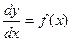 , dy = f(x)dx Общее решение , dy = f(x)dx Общее решение
|
| y=∫f(x)dx=F(x)+C
| |
|
|
|
| |
| 2 Дифференциальное уравнение типа у' = f(y)
 , , 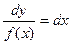 Общее решение
Общее решение
|
| 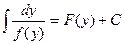
| |
| Дифференциальное уравнение с разделенными переменными
f(x) dx + φ(y)dy = 0
Общее решение
|
| ∫f(x) dx + ∫φ(y)dy = C, F(х) + Ф(у) = С
| |
| Дифференциальное уравнение с разделяющимися переменными
f(x)φ(y)dx+ψ(x)Ф(y)dy=0
Приведем это уравнение к уравнению с разделенными переменными
  Общее решение
Общее решение
|
|  F1(x)+F2(y)=C F1(x)+F2(y)=C
|
Теория вероятностей. Математическая статистика
|
| ВОПРОС
|
| ОТВЕТ
| |
| Относительная частота события
где п — число независимых испытаний, в которых случайное событие А происходит m раз.
|
| 
| |
| Вероятность случайного события
|
| 
| |
| Вероятность появления одного (безразлично какого) из нескольких несовместных событий (теорема сложения вероятностей). Для двух событий
|
| P( А и В) = Р(А) + Р(В).
| |
| Вероятность совместного появления независимых событий (теорема умножения вероятностей) Для двух событий
|
| P(А и В) = Р(А)Р(В].
| |
| Вероятность того, что событие А произойдет L раз при п испытаниях (биномиальное распределение)
|
|
 где Р — вероятность наступления события А.
где Р — вероятность наступления события А.
| |
| Распределением дискретной случайной величины называют
|
| совокупность ее значений: х1, х2, ... и соответствующих вероятностей:
p(x1)=p1, p(x2)=p2 ….
| |
| Условие нормировки для дискретной случайной величины, имеющей п значений
|
| 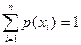
| |
| Среднее значение дискретной случайной величины
|
|
 где тi, — число дискретных случайных величин, имеющих значение xi. где тi, — число дискретных случайных величин, имеющих значение xi.
| |
| Математическое ожидание дискретной случайной величины
|
|

| |
| Дисперсия дискретной случайной величины
|
| D(X) = M{[X-M(X)]2},
D(X) = M(X2)-[M(X)]2,
| |
| Среднее квадратическое отклонение
|
|

| |
| Вероятность того, что непрерывная случайная величина принимает какое-либо значение в интервале (а, b)
|
|
 где f(x) — плотность вероятности (функции распределения вероятностей) где f(x) — плотность вероятности (функции распределения вероятностей)
| |
| Условие нормировки для непрерывной случайной величины
|
|
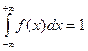
| |
| Функция распределения случайной величины
|
|

| |
| Математическое ожидание непрерывной случайной величины
|
|

| |
| Дисперсия непрерывной случайной величины
|
|

| |
| Нормальный закон распределения (закон Гаусса)
|
|   где а — математическое ожидание случайной величины,
σ - среднее квадратическое отклонение.
где а — математическое ожидание случайной величины,
σ - среднее квадратическое отклонение.
| |
| Функция распределения по нормальному закону
|
|  Значения функции Ф даны в табл Значения функции Ф даны в табл
| |
| Плотность вероятности для проекции скорости молекул газа
на ось Ох при тепловом движении (распределение Максвелла по скоростям)
|
|  где то — масса молекулы, Т — термодинамическая температура газа, k — постоянная Больцмана. где то — масса молекулы, Т — термодинамическая температура газа, k — постоянная Больцмана.
| |
| Плотность вероятности для модуля скорости молекул газа (распределение Максвелла по скоростям)
|
| 
| |
| Средняя, средняя квадратичная и навероятнейшая скорости молекул
|
|  где R — молярная газовая постоянная, М — молярная масса
где R — молярная газовая постоянная, М — молярная масса
| |
| Плотность вероятности нахождения молекулы газа в однородном гравитационном поле (пример распределения Больцмана)
|
| 
| |
| Давление газа (воздуха), находящегося в однородном гравитационном поле, на высоте h (барометрическая формула)
|
| 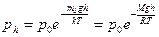 где рh— давление на высоте h=0 где рh— давление на высоте h=0
| |
| Концентрация молекул газа (воздуха), находящегося в однородном гравитационном поле, на высоте h
|
| 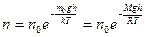 где nо — концентрация молекул газа на высоте h = О
где nо — концентрация молекул газа на высоте h = О
| |
| Интервальная оценка генеральной средней (среднее значение генеральной совокупности)
|
| ‹ xв› -ε< μ < ‹ xв› + ε,
где ‹ xв› — выборочная средняя Эти неравенства выполняются с доверительной вероятностью Р Положительное число ε характеризует точность оценки и называется доверительным интервалом
| |
| При большой выборке (n>30)
|
| 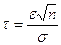 где σ — генеральное среднее квадратическое отклонение Обычно в расчетах берется выборочное среднее квадратическое отклонение
где σ — генеральное среднее квадратическое отклонение Обычно в расчетах берется выборочное среднее квадратическое отклонение
| |
| Связь между τ и P
|
| 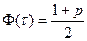 Значения функции Ф(τ) даны в табл
Значения функции Ф(τ) даны в табл
| |
| Интервальная оценка генеральной средней при малой выборке
n≤30
|
| 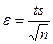 Здесь
Здесь  — исправленная выборочная дисперсия,
где σb2 — выборочная дисперсия
Параметр t (коэффициент Стьюдента) для заданных п и Р находят по табл — исправленная выборочная дисперсия,
где σb2 — выборочная дисперсия
Параметр t (коэффициент Стьюдента) для заданных п и Р находят по табл
|
МЕХАНИКА Кинематика
|
| ВОПРОС
|
| ОТВЕТ
| |
| Средняя скорость точки
|
| определяется отношением пути, пройденного точкой, ко времени, в течение которого этот путь пройден:

| |
| Физическая величина, характеризующая изменение скорости за единицу времени
|
| называется средним ускорением:
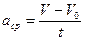 ,
где V и V0 — конечная и начальная скорости движения. ,
где V и V0 — конечная и начальная скорости движения.
| |
| В общем случае мгновенная скорость прямолинейного движения
|
| 
| |
| В общем случае мгновенное ускорение прямолинейного движения
|
| 
| |
| В случае прямолинейного равнопеременного движения скорость равна
|
|
 где V и V0 — конечная и начальная скорости движения.
где V и V0 — конечная и начальная скорости движения.
| |
| Путь, пройденный точкой при равнопеременном движении равен
|
|

| |
| При криволинейном движении точки абсолютная величина полного ускорения равна
|
|
 где
где  тангенциальное (касательное) ускорение; тангенциальное (касательное) ускорение;  нормальное (центростремительное) ускорение, где V0 - скорость движения; R — радиус кривизны траектории. нормальное (центростремительное) ускорение, где V0 - скорость движения; R — радиус кривизны траектории.
| |
| Простейшим видом криволинейного движения является
|
| равномерное движение точки по окружности.
При таком движении тангенциальное ускорение aτ = 0, нормальное ускорение, называемое в этом случае центростремительным,
аn = const.
| |
| Если точка движется по кругу радиуса R с линейной скоростью V, делая за время t n оборотов, то скорость равна
|
|
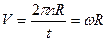 ,
где ,
где  - угловая скорость - угловая скорость
| |
| Кинематическими характеристиками вращательного движения тел служат
|
| угловое перемещение, угловая скорость и угловое ускорение
| |
| Угловым перемещением φ
|
| называется центральный угол, соответствующий дуге, пройденной движущейся точкой.
| |
| Средняя угловая скорость ωср и среднее угловое ускорение εср определяются
|
| аналогично средней скорости и среднему ускорению прямолинейного движения, т. е.
 и и  где ω и ω0 — конечная и начальная скорости углового движения.
где ω и ω0 — конечная и начальная скорости углового движения.
| |
| В общем случае угловая скорость криволинейного движения равна
|
|

| |
| В общем случае угловое ускорение криволинейного движения равна
|
|

| |
| В случае вращательного равнопеременного движения угловая скорость равна
|
| 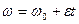
| |
| Угловое перемещение, пройденное точкой при равнопеременном вращательном движении равно
|
| 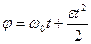
| |
| тангенциальное (касательное) ускорение;  нормальное (центростремительное) ускорение, где V0 - скорость движения; R — радиус кривизны траектории связаны с угловыми характеристиками соотношениями нормальное (центростремительное) ускорение, где V0 - скорость движения; R — радиус кривизны траектории связаны с угловыми характеристиками соотношениями
|
|


| |
| Изменение количества движения тела за определенный промежуток времени равно
|
| Импульсу действующей силы (второй закон Ньютона):
dk = Fdt,
где dk — изменение количества движения. F — равнодействующая всех сил, приложенных к телу массой т; dt — промежуток времени, в течение которого на тело действовала сила
| |
| Количество движения равно
|
| произведению массы тела на скорость его движения v, т. е. k = mv
| |
| Если масса тела постоянна, то второй закон динамики можно представить в виде
|
|
 где а — ускорение, приобретаемое телом массой m под действием силы F.
где а — ускорение, приобретаемое телом массой m под действием силы F.
| |
| Тело массой m, движущееся поступательно со скоростью V, обладает кинетической энергией
|
|

| |
| Потенциальная энергия тела, поднятого над поверхностью Земли (потенциальная энергия тела, находящегося на поверхности Земли, принимается равной нулю)
|
|  ,
где h — высота поднятия тела над поверхностью Земли;g - ускорение свободного падения. ,
где h — высота поднятия тела над поверхностью Земли;g - ускорение свободного падения.
| |
| Работу силы F при перемещении тела на пути s определяют по формуле
|
|

| |
| Работа постоянной силы выражается произведением силы, действующей в направлении перемещения, на величину этого перемещения s:
|
|
А = Fs cos a,
где а — угол между направлением действия силы и направлением перемещения
| |
| Если тело массой m изменило свою скорость под действием силы от V1 до V2, то работа силы равна
|
|

| |
| Мощность определяется по формуле
|
| 
| |
| в случае постоянной мощности, мощность определяется по формуле
|
| 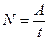 где А — работа , совершаемая за время t
где А — работа , совершаемая за время t
| |
| Центростремительная сила, действующая на тело, движущееся по кривой равна
|
|  где R — радиус кривизны. В случае движения тела по окружности он равен радиусу этой окружности.
где R — радиус кривизны. В случае движения тела по окружности он равен радиусу этой окружности.
| |
| Момент силы относительно оси вращения равен
|
| произведению силы F на
плечо I:
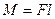 ,
где l— кратчайшее расстояние от оси вращения до линии действия силы. ,
где l— кратчайшее расстояние от оси вращения до линии действия силы.
| |
| Момент инерции J материальной точки равен
|
| произведению массы m материальной точки на квадрат расстояния r этой точки от оси вращения:
J=mr2
| |
| Момент инерции твердого тела равен
|
|
 где интегрирование должно проводиться по всему объему тела
где интегрирование должно проводиться по всему объему тела
| |
| Если для какого-либо тела известен его момент инерции J0 относительно оси, проходящей через центр тяжести, то момент инерции J относительно любой оси, параллельной первой, может быть найден по формуле
|
|
J = J0 + mа2,
где а — расстояние от центра тяжести тела до оси вращения; m — масса тела.
| |
| Момент инерции однородного шара радиусом R, массой m относительно оси, проходящей через центр массы:
|
|

| |
| Момент инерции однородного цилиндра с внутренним радиусом r и внешним R (ось враще ния совпадает с геометрической осью цилиндра), массой m относительно оси, проходящей через центр массы:
|
|

| |
|
|
|
| |
| момент инерции: тонкостенного цилиндра (R≈ г)
|
| J=mR2
| |
| момент инерции: сплошного цилиндра (г=0)
|
| 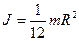
| |
| момент инерции: тонкого стержня длиной l (ось вращения проходит перпендикулярно стержню через его середину)
|
|
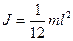
| |
| Изменение момента количества движения dL
|
| пропорционально величине приложенного момента силы и времени его действия (основное уравнение динамики вращательного движения):
dL = Mdt,
где dL — изменение момента количества движения. М — момент силы, приложенной к телу; dt — промежуток времени, в течение которого на тело действовала сила.
| |
| Момент количества движения L равен
|
| произведению момента инерции / на угловую скорость вращения ω0, т. е.
L = Jω0
| |
| Момент импульса (момент количества движения) материальной точки
|
| Li=miviri
| |
| Момент импульса тела
|
| 
| |
| Если момент инерции тела постоянен, то основное уравнение динамики вращательного движения можно записать в виде
|
| Jdω0 = Mdt или М =Jε,
где ε — угловое ускорение.
| |
| Для изолированного тела, способного изменять момент инерции при вращении, закон сохранения момента количества движения можно записать так
|
| L = const или Jω0 = const
| |
| Кинетическая энергия вращающегося тела
|
| 
| |
| Кинетическая энергия тела, вращающегося с угловой скоростью ω вокруг оси, при поступательном движении оси со скоростью v равно
|
|

| |
| Элементарная работа во вращательном движении равна
|
| dA=Mdφ
где М — момент силы, приложенной к телу.
| |
| Работа силы при вращательном движении равна
|
|  где углы φ1 и φ2 соответствуют начальному и конечному положениям радиуса-вектора любой точки твердого тела.
где углы φ1 и φ2 соответствуют начальному и конечному положениям радиуса-вектора любой точки твердого тела.
| |
| Сила, действующая на частицу со стороны окружающей жидкости, при центрифугировании равна
|
| F1 = ρ0Vω2r,
где ρ0 — плотность жидкости, V — объем частицы, ω — угловая скорость вращения, r — расстояние частицы от оси вращения.
| |
| Сила, действующая на частицу при ее движении по окружности при центрифугировании равна
|
| F = ρ1Vω2r,
где ρ1 — плотность вещества частицы.
| |
| При центрифугировании если сила, действующая на частицу со стороны окружающей жидкости F1 не равна силе, действующей на частицу при ее движении по окружности F, т.е. F1> F то
|
| происходит перемещение частицы в направлении к оси вращения
| |
| При центрифугировании если сила, действующая на частицу со стороны окружающей жидкости F1 не равна силе, действующей на частицу при ее движении по окружности F, т.е. F1<.F то
|
| происходит перемещение частицы в направлении от оси вращения
|
|
|

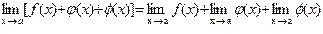

 при lim φ(x)≠0
при lim φ(x)≠0




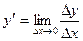
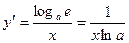














 ,
v = x
Используя формулу интегрирования по частям, получаем
у = ∫ Ln xdx = x Ln х-∫ dх = xLnx-x+C
,
v = x
Используя формулу интегрирования по частям, получаем
у = ∫ Ln xdx = x Ln х-∫ dх = xLnx-x+C
 Тогда
y=0,5∫z2dz
Тогда
y=0,5∫z2dz
 Возвращаясь к прежней переменной х, окончательно имеем
Возвращаясь к прежней переменной х, окончательно имеем


 где F′первообразная функцию f(x), т е
F′(x)=f(x)
где F′первообразная функцию f(x), т е
F′(x)=f(x)


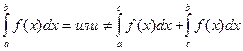




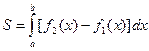
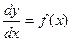 , dy = f(x)dx Общее решение
, dy = f(x)dx Общее решение
 ,
, 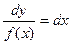 Общее решение
Общее решение
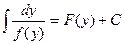
 Общее решение
Общее решение
 F1(x)+F2(y)=C
F1(x)+F2(y)=C


 где Р — вероятность наступления события А.
где Р — вероятность наступления события А.
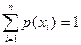
 где тi, — число дискретных случайных величин, имеющих значение xi.
где тi, — число дискретных случайных величин, имеющих значение xi.


 где f(x) — плотность вероятности (функции распределения вероятностей)
где f(x) — плотность вероятности (функции распределения вероятностей)
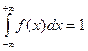




 где а — математическое ожидание случайной величины,
σ - среднее квадратическое отклонение.
где а — математическое ожидание случайной величины,
σ - среднее квадратическое отклонение.
 Значения функции Ф даны в табл
Значения функции Ф даны в табл
 где то — масса молекулы, Т — термодинамическая температура газа, k — постоянная Больцмана.
где то — масса молекулы, Т — термодинамическая температура газа, k — постоянная Больцмана.

 где R — молярная газовая постоянная, М — молярная масса
где R — молярная газовая постоянная, М — молярная масса

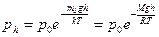 где рh— давление на высоте h=0
где рh— давление на высоте h=0
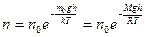 где nо — концентрация молекул газа на высоте h = О
где nо — концентрация молекул газа на высоте h = О
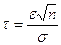 где σ — генеральное среднее квадратическое отклонение Обычно в расчетах берется выборочное среднее квадратическое отклонение
где σ — генеральное среднее квадратическое отклонение Обычно в расчетах берется выборочное среднее квадратическое отклонение
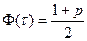 Значения функции Ф(τ) даны в табл
Значения функции Ф(τ) даны в табл
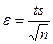 Здесь
Здесь  — исправленная выборочная дисперсия,
где σb2 — выборочная дисперсия
Параметр t (коэффициент Стьюдента) для заданных п и Р находят по табл
— исправленная выборочная дисперсия,
где σb2 — выборочная дисперсия
Параметр t (коэффициент Стьюдента) для заданных п и Р находят по табл

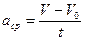 ,
где V и V0 — конечная и начальная скорости движения.
,
где V и V0 — конечная и начальная скорости движения.


 где V и V0 — конечная и начальная скорости движения.
где V и V0 — конечная и начальная скорости движения.

 где
где  тангенциальное (касательное) ускорение;
тангенциальное (касательное) ускорение;  нормальное (центростремительное) ускорение, где V0 - скорость движения; R — радиус кривизны траектории.
нормальное (центростремительное) ускорение, где V0 - скорость движения; R — радиус кривизны траектории.
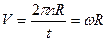 ,
где
,
где  - угловая скорость
- угловая скорость
 и
и  где ω и ω0 — конечная и начальная скорости углового движения.
где ω и ω0 — конечная и начальная скорости углового движения.


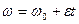
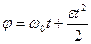


 где а — ускорение, приобретаемое телом массой m под действием силы F.
где а — ускорение, приобретаемое телом массой m под действием силы F.

 ,
где h — высота поднятия тела над поверхностью Земли;g - ускорение свободного падения.
,
где h — высота поднятия тела над поверхностью Земли;g - ускорение свободного падения.



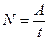 где А — работа , совершаемая за время t
где А — работа , совершаемая за время t
 где R — радиус кривизны. В случае движения тела по окружности он равен радиусу этой окружности.
где R — радиус кривизны. В случае движения тела по окружности он равен радиусу этой окружности.
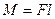 ,
где l— кратчайшее расстояние от оси вращения до линии действия силы.
,
где l— кратчайшее расстояние от оси вращения до линии действия силы.
 где интегрирование должно проводиться по всему объему тела
где интегрирование должно проводиться по всему объему тела


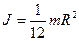
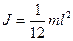



 где углы φ1 и φ2 соответствуют начальному и конечному положениям радиуса-вектора любой точки твердого тела.
где углы φ1 и φ2 соответствуют начальному и конечному положениям радиуса-вектора любой точки твердого тела.