|
|
Программирование алгоритмов разветвляющейся структурыПример. Вычислить значение функции.
а) с использованием условного оператора if-then-else
n:integer;
x:=ln(abs(a-cos(a)));
begin y:=-10.5; n:=1; end
else
end.
x=1.927 c=14.162 y=16.389 n=3
б) c использованием оператора выбора case
var a,b,c,x,y:real;
write(‘Введите а=’); readln(a); x:=ln(abs(a-cos(a)));
if c<=3.5 then k:=2 else k:=3;
Введите а=7.35
y=16.389 k=3
нет
k=2
Суммирование рядов
Задача. Разработать программу вычисления точного Y и прибли-женного S значений функции при изменении её аргумента от xн до xк с шагом Δx. Приближенное значение функции, представленной бесконечным рядом Ниже рассмотрены примеры суммирования бесконечных рядов трех типов: а) текущий член ряда ai вычисляется непосредственно; б) текущий член ряда ai вычисляется по рекуррентной формуле
где в) текущий член ряда ai является произведением двух сомножителей где Примеры а) рассматривается вариант вычисления суммы бесконечного ряда, текущий член ai которого вычисляется непосредственно и имеет вид, например,
Пример 1.
б) рассматривается вариант вычисления суммы бесконечного ряда, текущий член ai которого содержит степенные выражения, факториалы и имеет вид, например.
Пример 2.
Рекуррентная формула
Проверка
в) рассматривается вариант вычисления суммы бесконечного ряда, текущий член ai которого содержит выражения, вычисляемые непосредственно, и выражения с факториалами и степенями и имеет вид, например,
Пример 3.
Решение
Вывод формулы итерации: 1. Определение типа члена ряда.
2. Определение формулы итерации в виде:
Формула итерации:
3. Проверка:
label met; var x,y,s,xn,xk,dx,c,a: real;
readln(xn,xk,dx);
for i:=1 to n do
  да begin c:=-x*x*c; да begin c:=-x*x*c;
a:=c/(2*i+1); if abs(a)<e then goto
met: writeln(‘x=’,x:3:1, ‘ y=’y:8:5,’ s=’,s:8:5,
x:=x+dx;
Результаты Введите xn,xk,dx=0.2 0.8 0.2
x=0.8 y=0.67474 s=0.67480 i=13
Задача. Разработать программу решения 4-х взаимосвязанных задач 1) расчёт элементов квадратной матрицы A=a(i,j), i,j=1,2,… по заданной формуле;
2) вычисление элементов вектора X=x(i) i=1,2,… по заданному правилу;
3) упорядочение элементов матрицы А или вектора Х;
4) вычисление значения функции y по заданной формуле.
Пример. 1)
2)
3) упорядочить элементы второго столбца матрицы А по убыванию значений;
4)
Задание выполнить для n=6. Замечание. Предварительно провести отладку программы при n=3, для чего получить решение задачи вручную (или с помощью калькулятора) и проверить полученные данные на ЭВМ.

 да да
Паскаль-программа program prim5; var a:array[1..10,1..10] of real; x:array [1..10] of real; i,j,k,n:integer; y,s,c:real; begin writeln(‘Введите n’); read(n); {---------------------------------------часть 1-----------------------------------} for i:=1 to n do for j:=1 to n do a[i,j]:=(2*j*i+4*i)/j; writeln(‘ ‘:20,’МАТРИЦА А’); for i:=1 to n do begin for j:=1 to n do write(a[i,j]:8:3); writeln; end; {---------------------------------------часть 2-----------------------------------} for i:=1 to n do begin s:=0; for j:=1 to n do s:=s+sqr(a[i,j]); x[i]:=sqrt(s)/n; end; writeln(‘ ‘:20,’ВЕКТОР Х’); for i:=1 to n do write(x[i]:8:3); {---------------------------------------часть 3-----------------------------------} for i:=1 to n-1 do begin k:=i; for j:=i+1 to n do if a[j,2]>a[k,2] then k:=j; if i<>k then begin c:=a[i,2]; a[i,2]:=a[k,2]; a[k,2]:=c; end; end; writeln(‘ ‘:14,’УПОРЯДОЧЕННАЯ МАТРИЦА’); for i:=1 to n do begin for j:=1 to n do write(a[i,j]:8:3); writeln; end; {---------------------------------------часть 4-----------------------------------} y:=1; for i:=1 to n do begin s:=0; for k:=1 to n do s:=s+x[k]; if x[i]<>0 then y:=y*x[i]*s; end; writeln(‘ЗНАЧЕНИЕ ФУНКЦИИ У=’,y:1:3); end.
Результаты Введите n=6 МАТРИЦА А 6.000 4.000 3.333 3.000 2.800 2.667 12.000 8.000 6.667 6.000 5.600 5.333 18.000 12.000 10.000 9.000 8.400 8.000 24.000 16.000 13.333 12.000 11.200 10.667 30.000 20.000 16.667 15.000 14.000 13.333 36.000 24.000 20.000 18.000 16.800 16.000
ВЕКТОР X 1.555 3.110 4.665 6.220 7.776 9.331
УПОРЯДОЧЕННАЯ МАТРИЦА А 6.000 24.000 3.333 3.000 2.800 2.667 12.000 20.000 6.667 6.000 5.600 5.333 18.000 16.000 10.000 9.000 8.400 8.000 24.000 12.000 13.333 12.000 11.200 10.667 30.000 8.000 16.667 15.000 14.000 13.333 36.000 4.000 20.000 18.000 16.800 16.000
ЗНАЧЕНИЕ ФУНКЦИИ Y=123454118108000.000 Список рекомендуемой литературы
1. Задания для практических и лабораторных занятий по информатике (работы 1-5): Методические указания./ Cост. Т.Г. Умергалин, И.Г. Мухамадеев, Э.В. Писаренко - Уфа: изд-во УГНТУ,1997.-51 с. 2. Основы программирования и работы в интегрированной среде Турбо-Паскаль: Методические указания./ Cост Т.Г. Умергалин, И.Г. Мухамадеев - Уфа: изд-во УГНТУ,1992.-45 с. 3. Емелина Е.И. Основы программирования на языке Паскаль. - М.: Финансы и статистика, 1997.-208 с. 4. Фаронов В.В. Турбо Паскаль: В 3-х кн. Кн. 1. Основы Турбо Паскаля. – М.: Учебно-инженерный центр “МВТУ-ФЕСТО ДИДАКТИК”,1992. – 304 с.
12 |
|


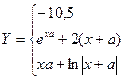


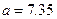
 Паскаль-программа
Паскаль-программа Program prim21;
Program prim21; var a,b,c,x,y:real;
var a,b,c,x,y:real; begin
begin
 c:=x*a; b:=x+a;
c:=x*a; b:=x+a; else
else if c=>3.5 then
if c=>3.5 then
 да begin y:=c+ln(b); n:=3; end
да begin y:=c+ln(b); n:=3; end нет begin y:=exp(c)+2*b; n:=2; end;
нет begin y:=exp(c)+2*b; n:=2; end; writeln(‘x=’,x:1:3,’ c=’,c:1:3,’ y=’,
writeln(‘x=’,x:1:3,’ c=’,c:1:3,’ y=’,
 да y:1:3,’ n=’,n);
да y:1:3,’ n=’,n); нет
нет







 Паскаль-программа
Паскаль-программа
 Program prim22;
Program prim22; k:integer;
k:integer;
 case k of
case k of 1: y:=-10.5;
1: y:=-10.5; да 2: y:=exp(c)+2*b;
да 2: y:=exp(c)+2*b; 3: y:=c+ln(b);
3: y:=c+ln(b); да writeln(‘x=’,x:1:3,’ c=’,c:1:3,’
да writeln(‘x=’,x:1:3,’ c=’,c:1:3,’ =’,y:1:3,’ k=’,k);
=’,y:1:3,’ k=’,k);
 x=1.927 c=14.162
x=1.927 c=14.162










 , вычислять путем суммирования членов ряда до достижения требуемой точности
, вычислять путем суммирования членов ряда до достижения требуемой точности 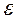 =
=  . То есть прибавлять очередной член ряда до тех пор, пока его значение по абсолютной величине не станет меньше
. То есть прибавлять очередной член ряда до тех пор, пока его значение по абсолютной величине не станет меньше  =1000.
=1000. ,
, ;
;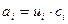 , где
, где  вычисляется непосредственно, а
вычисляется непосредственно, а 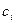 -по рекуррентной формуле. Формула итерации для текущего члена находится в виде:
-по рекуррентной формуле. Формула итерации для текущего члена находится в виде:  ,
, .
. и т.д.
и т.д. ;
;  ;
; ;
; - вычисляется непосредственно;
- вычисляется непосредственно;
 и т.д.
и т.д.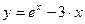 ;
; 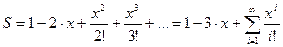 ;
;
 - вычисляется по рекуррентной формуле в виде:
- вычисляется по рекуррентной формуле в виде:
 ,
, 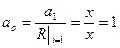 ;
; ;
; - формула верна;
- формула верна;
 и т.д.
и т.д. ;
;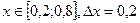 .
.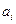 - смешанный тип
- смешанный тип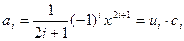 ,где
,где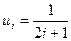 – вычисляется непосредственно, а
– вычисляется непосредственно, а - по рекуррентной формуле.
- по рекуррентной формуле.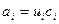 ,
,  ,
, 
 ,
, 
 ,
, 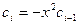 ,
, 
 .
. ,
,  - формула верна.
- формула верна. Блок-схема алгоритма Паскаль-программа
Блок-схема алгоритма Паскаль-программа const n=1000; e=0.0001
const n=1000; e=0.0001

 while x<=xk do
while x<=xk do нет begin
нет begin
 y:=arctan(x); s:=x; c:=x;
y:=arctan(x); s:=x; c:=x;
 met; s:=s+a;
met; s:=s+a; ’ i=’,i);
’ i=’,i); end
end


 end.
end.



 x=0.4 y=0.38051 s=0.38048 i=4
x=0.4 y=0.38051 s=0.38048 i=4
 да x=0.6 y=0.54042 s=0.54044 i=7
да x=0.6 y=0.54042 s=0.54044 i=7





 ;
;  ;
; ;
;  ;
;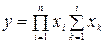 ;
;  .
. Блок-схема алгоритма
Блок-схема алгоритма






 нет
нет




 да
да







 нет
нет





 да
да




