|
|
Относительные уровни издержек на предприятиях 10 глава
откуда следует, что х = 48 годам.
214. На все привилегированные акции дивиденд составит:
6 х 5 % = 30 % от 100 млн руб., или 30 млн руб.
На все обыкновенные акции при этом останется для выплат дивидендов
100 млн руб.– 30 млн руб. = 70 млн руб.
Таким образом, на одну обыкновенную акцию придется дивиденд, равный
70 млн руб.: 28 = 2,5 млн руб.
На одну привилегированную акцию дивиденд равен 5 % от 100 млн руб., т. е. 5 млн руб.
215. 1) Курс акций (Ка) рассчитывается по формуле:
где Д – дивиденд, СП – ссудный процент. ;
Курсовая стоимость акции 30 тыс. руб. 2) Учредительская прибыль (УП) рассчитывается по формуле:
где СЦк и СЦн – суммарная цена по курсу и по номиналу соответственно.
Стоимость единицы продукции равна:
1) При росте производительности труда в три раза будет выпускаться 30 единиц продукции в день, и стоимость единицы продукции станет
а стоимость массы продукции – 30 х 1 = 30 тыс. руб.
2) При увеличении интенсивности труда в два раза 10 единиц продукции будет производиться за полдня, а в день будет произведено 20 единиц продукции. Следовательно, стоимость единицы продукции станет
а стоимость массы продукции – 20 x 1,5 = 30 тыс. руб.
217. 1) Норма прибыли (НП) рассчитывается по формуле:
где П – прибыль, З – затраты. С учетом того, что З = В - П, где В – величина выручки, получим:
Сумма эмиссии равна: П + 4 % П = 50 + 2 = 52 млн руб. 2) Общая стоимость привилегированных акций: 100 х 100 тыс. руб. = 10 млн руб. При этом на обыкновенные акции остается 52 - 10 = 42 млн руб., что дает возможность выпустить 42 : 0,5 = 84 обыкновенные акции.
218. 1) Курс акций рассчитывается по формуле (см. решение задачи 215):
Курсовая цена акции при этом 200 тыс. руб. 2) Учредительская прибыль рассчитывается по формуле (см. решение задачи 215):
219. Если бы у партнеров было 8 общих счетов, Семенов израсходовал бы их за 12 х 8 = 96 месяцев. А Семенов и Федоров за 96 месяцев израсходовали бы деньги с Теперь понятно, что за эти же 96 месяцев Федоров израсходовал бы деньги с 12 - 8 = 4 счетов. Отсюда получается, что один счет Федоров способен израсходовать за 220. 1 каменщик выложит 2 м стены за 4 часа, 1 м – за 2 часа, 5 м – за 10 часов; 2 каменщика выложат 5 м стены за 5 часов. 221. Все три проекта вполне реальны. Первый проект изучается странами Аравийского полуострова. Второй проект не экономичен: на каждый подъем и спуск аэростата расходуется много энергии. Третий проект запатентован и опробуется в нашей стране. 222. 1) Прибыль рассчитывается по формулам (см. решение задачи 171):
Для того чтобы 6,1 % составили 1 млн руб., нужно получить доход (сумму выручки от реализации книги), равный
Для этого цена одной книги при тираже 100 тыс. экз. должна быть:
С учетом НДС: 164 + 20 % = 197 руб. 2) Авторский гонорар равен 3–5 % от 16,4 млн руб., т. е. 492-820 тыс. руб. 3) На бумагу, картон и другие материалы будет выделено 20 % от 16,4 млн руб., т. е. 3,28 млн руб. 4) Типографские расходы составят 30 % от 16,4 млн руб., т. е. 4 млн 920 тыс. руб. Издательские расходы составят 10–12 % от 16,4 млн руб., т. е. 1 млн 640 тыс.– 1 млн 968 тыс. руб. 5) Торговым организациям придется заплатить 25 % от 16,4 млн руб., т. е. 4 млн 100 тыс. руб. 6) Расходы на маркетинг, включая рекламу, равны 1 % от 16,4 млн руб., т. е. 164 тыс. руб. 7) При установлении цены книги 300 руб. ее цена без учета НДС составит Сумма выручки от реализации книги будет 250 руб. х 0,1 млн экз. = 25 млн руб. Чистая прибыль, равная 6,1 % от 25 млн руб., составит 1 млн 525 тыс. руб.
223. 9 часов. 224. Предположим, рассматривается экономия энергетических ресурсов, эквивалентных 100 тоннам топлива. Тогда в результате реализации первого предложения можно будет обойтись 65 тоннами топлива (100 - 35 %), после реализации второго предложения – 32,5 тонны (65 - 50 % от 65), после реализации третьего – 27,7 тонны (32,5 - 15 % от 32). Таким образом, общая экономия составит 100-27,7 = 72,3%. 225. Поскольку каждый должен вложить равную долю – 150 тыс. руб., то долг третьего компаньона первому составляет 230 - 150 = 80 тыс. руб., а второму – 220-150 = 70 тыс. руб. 226. Доля каждого предприятия составляет Отсюда стоимость 1 блока равна:
Из этого следует, что первое предприятие затратило 70 блоков по 3 тыс. у. д. ед., т. е. 210 тыс. у. д. ед.; второе – 40 блоков по той же цене, т. е. 120 тыс. у. д. ед.; третье, как известно, затратило 110 тыс. у. д. ед. Очевидно, что третье предприятие должно первому 100 тыс. у. д. ед. (210-110) и второму 10 тыс. у. д. ед. (120-110). 227. Наливаем в соответствующую емкость ровно 8 литров вина, из которой отливаем в 5-литровую ровно 5 (при этом в 8-литровой емкости остается ровно 3 литра). Из 5-литровой емкости вино переливаем в 12-литровую и в освободившийся сосуд наливаем оставшиеся в 8-литровой емкости 3 литра. Снова из 12-литровой заполняем вином 8-литровую емкость, из которой заливаем доверху 5-литровую (в которой уже есть 3 литра). При этом в 8-литровой емкости остается ровно 6 литров.
228. Обозначим новый результат фермера – количество ежедневно вспахиваемой земли – через х. Тогда величина участка будет равна 8х (теперь он вспахивает его за 8 дней), и условие задачи можно записать так:
Из этого следует, что 1) х = 10 га, 2) величина участка равна 8х = 80 га. 229. Принимая количество автобусов, выпускаемых в день до реконструкции предприятия, можно записать условие задачи в виде следующего уравнения:
Отсюда х = 1, а количество автобусов, выпускаемых в день после реконструкции, равно х + 1 = 2. 230. Принимая количество изделий, выпускаемых в день по норме, за х, можно записать условие задачи в виде следующего уравнения:
откуда х = 2. Количество изделий, выпускаемых в день, фактически равно х + 3 = 5.
231. Принимая вес, потерянный яблоками после сушки, за х, можно записать условие задачи следующим образом:
Откуда х = 3, а искомый вес 4 т яблок после сушки равен 4 - 3 = 1 т. 232. Последовательность решения задачи такова: 1) Одна корова большого стада (70 коров) могла бы питаться травой 1680 дней (24 дня х 70 коров). 2) Одна корова малого стада (30 коров) могла бы питаться травой 1800 дней (60 дней х 30 коров). 3) Следовательно, за 36 дней (60 - 24) успевает нарасти трава, достаточная для питания одной коровы в течение 120 дней (1800-1680). 4) Значит, и за последующие 36 дней (96 -60) нарастет столько же травы, сколько хватит одной корове на 120 дней. 5) А всего количество дней, в течение которых могла бы питаться травой одна корова искомого стада, составит:
1800 + 120 = 1920 дней. 6) Зная, что коровы искомого стада будут питаться травой 96 дней, нетрудно найти, сколько в этом стаде коров: 1920 дней : 96 дней = 20 коров. 233. Первоначальное количество зеленой краски обозначим через х, тогда количество желтой составит 1 - х. После добавления 1 - х зеленой и х желтой краски количество красок разных цветов уравнялось (стало равным по 1). Следовательно, по 50 % краски каждого цвета.
234. В тонне сахара при влажности 15 % содержится 150 кг воды и 850 кг сухого вещества. После просушки количество воды уменьшилось на 80 кг и стало равно 70 кг. Следовательно, теперь влажность сахара составляет:
235. Вес жидкости в изделии до его сушки составлял 6 кг. Обозначая потери жидкости при сушке через х, можно записать условие задачи так:
Откуда х = 5,45 кг. Следовательно, вес изделия после сушки равен: 60 - 5,45 = 54,55 кг.
236. В одной тонне переработанного сырья по условию задачи содержится 0,17 т жидкости и 0,83 т сухого вещества. С учетом этого обстоятельства и принимая за х вес испарившейся в процессе переработки жидкости, можно записать условие задачи так:
Откуда х= 1,77 т. Следовательно, для того чтобы получить одну тонну продукта, нужно переработать сырья 1 + 1,77 = 2,77 т. 237. В 100 т морской воды по условию задачи содержится 6 т соли. С учетом этого обстоятельства и принимая за х количество пресной воды, необходимое для опреснения, можно записать условие задачи так:
Откуда х = 500 т.
238. В слитке сплава по условию задачи содержится 4 кг золота. С учетом этого обстоятельства и принимая за х количество золота, которое нужно добавить к слитку, можно записать условие задачи так:
Откуда х = 20 кг.
239. Принимая первоначальный вес сахара за х, а вес сахара после просушки за x1, можно записать условие задачи так:
Следовательно, вес высушенного сахара стал на 9 % меньше первоначального. 240. Раньше 5 деталей из 100 были с браком, теперь 1 деталь из 100. Следовательно, брак сократился на
241.Примем старое количество единиц продукции, выпускаемых в единицу времени, за 1. При этом время, затрачиваемое на единицу продукции, равно 1. Новое количество единиц продукции стало 1,5. Значит, теперь время, затрачиваемое на единицу продукции, равно
243. Первый экскаватор проработал на 4 часа меньше нормы и в результате недоработал 40 % задания. Значит, первый экскаватор способен выполнить 100 %задания за
А за 8 часов первый экскаватор отработает 80 % задания. Это означает, что второй экскаватор за 8 часов выполнил 100 - 80 = 20 % задания. А 100 % задания второй экскаватор выполнит за
244. Принимая работу, выполненную бригадой № 1 в час, за единицу, можно записать, что обе бригады в час выполняют:
А за 10 часов обе бригады выполняют:
Следовательно, бригада № 1 смогла бы самостоятельно выполнить данную работу за 23 : 1 = 23 часа, бригада № 2 - за 23 : 1,3 = 17,7 часа.
245. Принимая сторону садового участка до увеличения за 1, получим его периметр, равный 4, а площадь – 1. С увеличением периметра на 20 % его стороны также вырастут на 20 % и станут равны 1,2. Площадь при этом будет равна (1,2)2 = 1,44, т. е. вырастет на 44 %.
246. Принимая сторону садового участка до увеличения за единицу, получим его площадь, равную единице. Площадь участка с увеличением на 40 % его сторон станет равна 1,4 х 1,4 = 1,96, т. е. вырастет на 96 %.
247. Принимая сторону прямоугольного садового участка до увеличения за единицу, получим его площадь, равную единице. С изменением сторон участка его площадь станет равна 1,3 х 0,7 = 0,91, т. е. уменьшится на 9 %.
248. Находим, какие доли дома строительные организации строят за один год, и суммируем эти доли:
Исходя из того, что эта суммарная доля строится за 365 дней, рассчитываем (из пропорции), за сколько дней строится единица дома:
249.
250. Поскольку копия легче натуры в 8 миллионов раз и сделана из того же металла, то ее объем должен быть меньше объема натуры тоже в 8 миллионов раз. Но объемы тел относятся, как кубы их высот. Следовательно, копия должна быть ниже натуры в
Высота Эйфелевой башни около 300 м, поэтому высота копии должна быть 251. Поскольку объемы тел относятся, как кубы их линейных размеров, большая емкость должна быть в 252. Объем меньшего блока будет в 53 = 125 раз меньше. Следовательно, он будет весить
253. Обозначим через х количество спирта, который отлили в первый раз, и количество смеси, отлитой во второй раз. Тогда после первого отливания в емкости останется 100 - х спирта, а после доливания в нее воды в каждом литре смеси будет содержаться
литров спирта. После следующего отливания х литров смеси в емкости останется 100 - х литров смеси, в которой будет содержаться
литров спирта. Затем после второго доливания воды в емкости будет 100 литров смеси, из которых
Известно, что это соответствует 49-процентному раствору спирта:
Откуда х = 30 литров. 254.Примем площадь большого луга за единицу. Так как этот луг полдня косила вся артель и еще полдня – пол-артели, то, значит, за полдня пол-артели скашивает – большого луга. Следовательно, участок, не докошенный половиной артели на малом лугу, равен Это и есть дневная норма одного косца. А количество косцов в среднем можно найти, разделив то, что они выкосили за один день
255. Обозначим через х искомое количество граммов компонента коктейля с 50 % спирта, а через у – с 20 % спирта. Тогда условие задачи можно записать в виде следующего уравнения:
Из этого уравнения следует, что у = 2х, т. е. количество 50-процентного компонента коктейля должно быть в 2 раза меньше, чем 20-процентного. Так, в килограмме коктейля должно быть 333 г 50-процентного компонента и 667 г – 20-процентного.
256. Обозначив через х первоначальное количество топлива в баке «КамАЗа» и через у – в баке «Икаруса», можно составить по условиям задачи следующие два уравнения:
Совместное решение уравнений (1) и (2) приводит к ответу:
ПРИЛОЖЕНИЕ К РЕШЕНИЯМ
Таблица сложных процентов
|
|
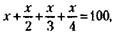


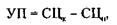

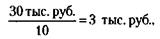
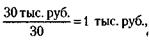

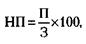
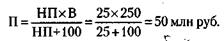

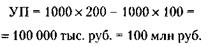
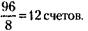
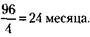
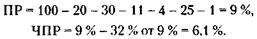
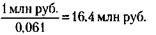
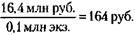
 руб.
руб. блоков, которые стоят 110 тыс. у. д. ед.
блоков, которые стоят 110 тыс. у. д. ед.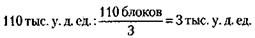
 – старый результат фермера.
– старый результат фермера.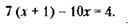
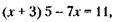
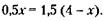
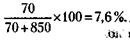
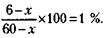
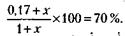

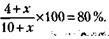
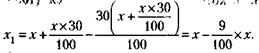
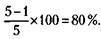
 = 0,67, т. е. сократилось на 33 %.
= 0,67, т. е. сократилось на 33 %.

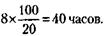

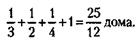
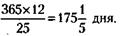
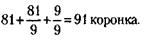
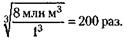
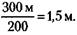
 = 3 раза выше и шире. Поверхности же подобных тел относятся как квадраты линейных размеров, т. е. поверхность большей емкости в З2 = 9 раз больше, а значит, и в 9 раз тяжелее.
= 3 раза выше и шире. Поверхности же подобных тел относятся как квадраты линейных размеров, т. е. поверхность большей емкости в З2 = 9 раз больше, а значит, и в 9 раз тяжелее.
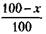
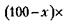
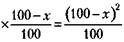
 литров составит спирт. Следовательно, процентное содержание спирта теперь равно
литров составит спирт. Следовательно, процентное содержание спирта теперь равно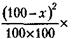
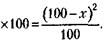
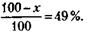
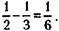
 на дневную норму косца:
на дневную норму косца: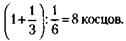
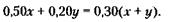
 (1) (2)
(1) (2)