|
|
Структурный подход к разработке алгоритмовРеальные алгоритмы и вычислительные процессы представляют собой совокупность всех рассмотренных базовых структур. Все базовые структуры имеют один вход и один выход. Таким образом, любую базовую структуру можно представить в виде функционального модуля, также имеющего один вход и один выход (рис. 25). Для графического изображения функциональных модулей в схемах алгоритмов используется символ предопределенного процесса.

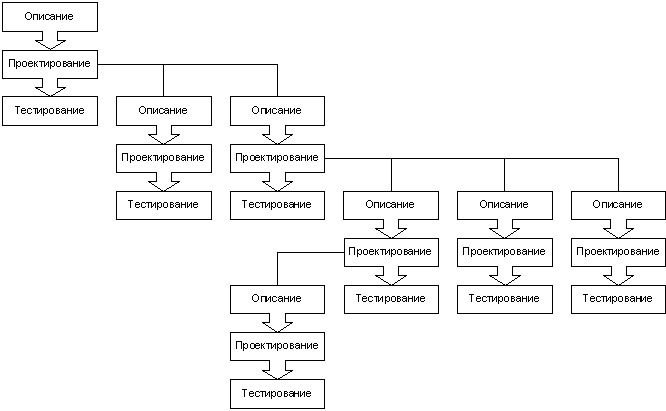
Рисунок 25 -Преобразование базовых структур Совокупность функциональных модулей, в свою очередь, может образовывать рассмотренные выше базовые структуры, которые также могут быть представлены в виде функциональных модулей (в качестве примера на рис. 6 приведено преобразования базовой структуры следование, состоящей из функциональных модулей в один функциональный модуль). Говоря другими словами, одна базовая структура может быть вложена в другую базовую структуру. Последовательное объединение базовых структур в функциональные модули в конечном итоге приводит к тому, что любой алгоритм может быть представлен одним функциональным блоком-модулем. При этом преобразование является дуальным, т.е. возможно обратное преобразование. При разработке любого алгоритма первоначально определяются исходные данные, требуемый результат и основные этапы, приводящие к решению поставленной задачи. При дальнейшей разработке необходимо придерживаться принципа постепенной детализации функциональных модулей, из которых составлялся первоначальный вариант алгоритма. Такая разработка алгоритмов получила название нисходящего (“сверху вниз”) проектирования, пример которого показан на рис. 26.
Рисунок 26 - Нисходящее проектирование
Процесс проектирования начинается с составления спецификации и проектирования головного алгоритма. Затем для каждого функционального модуля головного алгоритма в свою очередь определяются спецификации и выполняется проектирование. Процесс продолжается до достижения приемлемого уровня детализации. При этом, в отличие от восходящего проектирования, заключающегося в объединении функциональных модулей в единый алгоритм, изменение в спецификациях, вызванных изменениями в более высокой иерархии алгоритма, менее вероятно. Таким образом, функциональный модуль представляет собой совокупность логически связанных операций или функциональных модулей, выполняющих некоторое законченное действие.

Рисунок 27 – Преобразование неструктурного алгоритма
В теории алгоритмов доказано, что любой алгоритм можно представить композицией всего лишь четырех базовых структур: СЛЕДОВАНИЕ, ВЕТВЛЕНИЕ, ЦИКЛ-ДО и ЦИКЛ-ПОКА. Строгое структурное проектирование определяет использование только этих структур (при этом следует отметить, что рассмотренная выше структура обход не является базовой). Однако в практике проектирования алгоритмов часто возникают типовые ситуации, такие, например, как досрочный выход из цикла, обход и прочие. Они легко преобразуются в структурные схемы, однако часто при этом теряется наглядность алгоритма (рис. 27). Поскольку нестандартные алгоритмы также имеют один вход и выход, то нестрогое структурное проектирование допускает их разумное использование. В качестве примера структурного подхода рассмотрим решение следующей задачи: Вывести на печать таблицу значений функции
Разработка алгоритма начинается с выделения основных этапов. Первоначально можно выделить два этапа: ввод исходных данных и вычисление таблицы значений функции. Проанализировав задачу и определив исходные данные для ее решения, составим спецификацию на алгоритм для первого уровня детализации. Назначение: построение таблицы значений функции. Метод решения: неизвестен (определяется функциональным модулем). Входные данные: n, y, xmin, xmax, Dx. Выходные данные: нет (определяются функциональным модулем). Литература: нет. Построим алгоритм по данной спецификации (рис. 28, а). Выполним детализацию функционального модуля 3. Построение таблицы значений функции f(x,y) состоит из цикла с параметром x. В теле цикла, в зависимости от значения x, вычисление ведется по одному из двух выражений, то есть внутри цикла имеет место ветвление (на данном этапе можно было бы ограничиться лишь циклом, однако предлагаемый уровень детализации не ухудшает наглядность алгоритма). Назначение: построение таблицы значений функции. Метод решения: ветвление в цикле. Входные данные: n, y - для вычисления выражений; xmin, xmax, Dx - параметры цикла. Выходные данные: значения f(x,y) для каждого значения х. Литература: нет. Алгоритм, раскрывающий функциональный модуль 3 и разработанный с учетом вышеприведенной спецификации, приведен на рис. 28, б. Дальнейшей детализации требуют блоки 3 и 4. Алгоритмы для расчета суммы в обоих случаях идентичны и представляют собой цикл, в котором выполняется суммирование и вычисление очередного значения y. Назначение: вычисление значения функции. Метод решения: суммирование в цикле. Входные данные: n - верхний предел суммирования; x - значение первой переменной; y - значение второй переменной. Выходные данные: значение f(x,y). Литература: нет. Перед началом цикла (рис. 28, в, г) обнуляется значение переменной f, а значение переменной z, введенной для рекуррентного подсчета yi, приравнивается значению y. Переменная z введена для того, чтобы не изменилось исходное значение y.

Рисунок 28 – Подетальная разработка алгоритма
|
|
 , где значение x изменяется в диапазоне от
, где значение x изменяется в диапазоне от 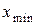 до
до  с шагом
с шагом  ;
; 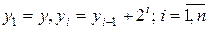 ; для функции, имеющей вид:
; для функции, имеющей вид: