|
|
Интерференция в плоскопараллельной пластинеОбщие методические указания
При решении и оформлении задач необходимо соблюдать следующие требования: 1. Записать краткое условие задачи, выразить все известные величины в одной и той же системе единиц (как правило, в СИ). При необходимости ввести дополнительные постоянные физические величины. 2. Решение задач следует сопровождать краткими, но исчерпывающими объяснениями. При необходимости дать чертеж или график. 3. Решать задачу надо в общем виде, т.е. выразить искомую величину в буквенных обозначениях величин, заданных в условии задачи. Произвести вычисления по расчетной формуле с соблюдением правил приближенных вычислений. Результаты контроля аудиторной и самостоятельной работы студентов на практических занятиях учитываются лектором при приеме экзаменов и дифференцированных зачетов.
ИНТЕРФЕРЕНЦИЯ СВЕТА
Основные формулы и законы
• Скорость света и длина волны в среде
где • Оптическая длина пути световой волны
где • Оптическая разность хода двух световых волн
• Зависимость разности фаз
где • Условие интерференционных максимумов
• Условие интерференционных минимумов
· Координаты максимумов и минимумов интенсивности в опыте Юнга
где • Ширина интерференционной полосы
· Оптическая разность хода при интерференции в тонких плёнках в проходящем свете:
в отражённом свете:
где • Радиусы светлых колец Ньютона в отраженном свете (или темных в проходящем свете)
где • Радиусы темных колец Ньютона в отраженном свете (или светлых в проходящем свете)
• В случае «просветления оптики» интерферирующие лучи в отраженном свете гасят друг друга при условии
где
Задания Опыт Юнга 1.1. Расстояние от щелей до экрана в опыте Юнга равно 1 м. Определить расстояние между щелями, если на отрезке длиной 1 см укладывается 10 темных интерференционных полос. Длина волны равна 0,7 мкм. [0,63 мм]. 1.2. Две когерентные световые волны приходят в некоторую точку пространства с разностью хода 2,25 мкм. Каков результат интерференции в этой точке, если свет: а) красный (l= 750 нм), б) зеленый (l= 500 нм)? [а) усиление; б) ослабление]. 1.3. Разность хода двух интерферирующих лучей монохроматического света 0,3l. Определить разность фаз колебаний. [108°]. 1.4.Расстояние между двумя щелями в опыте Юнга равно 1 мм, расстояние от щелей до экрана 3 м, расстояние между максимумами яркости смежных интерференционных полос на экране 1,5 мм. Определить длину волны источника монохроматического света. [500 нм]. 1.5.В опыте Юнга расстояние между щелями равно 1 мм, а расстояние от щелей до экрана равно 3 м. Определить: 1) положение первой светлой полосы; 2) положение третьей темной полосы, если щели освещать монохроматическим светом с длиной волны 0,5 мкм. [1) ±1,5 мм; 2) ±5,25 мм]. 1.6.Расстояние между двумя щелями в опыте Юнга равно 0,5 мм. Длина волны света равна 0,6 мкм. Определить расстояние от щелей до экрана, если ширина интерференционных полос равна 1,2 мм. [1 м]. 1.7.Во сколько раз изменится ширина интерференционных полос на экране в опыте с зеркалами Френеля, если фиолетовый светофильтр (0,4 мкм) заменить красным (0,7 мкм). [1,75]. 1.8.Во сколько раз увеличится расстояние между соседними интерференционными полосами на экране в опыте Юнга, если зеленый светофильтр (l=0,5 мкм) заменить красным (l=0,65 мкм)? [В 1,3 раза]. 1.9.В опыте Юнга отверстия освещались монохроматическим светом длиной волны 600 нм, расстояние между отверстиями 1 мм и расстояние от отверстий до экрана 3 м. Найти положение трех первых полос. [1,8 мм; 3,6 мм; 5,4 мм]. 1.10.В опыте с зеркалами Френеля расстояние между мнимыми изображениями источника света равно 0,5 мм, расстояние от них до экрана равно 5 м. В желтом свете ширина интерференционных полос равна 6 мм. Определить длину волны света. [0,6мкм]. 1.11.Если в опыте Юнга на пути одного из интерферирующих лучей поместить перпендикулярно этому лучу тонкую стеклянную пластинку (n=1,5), то центральная светлая полоса смещается в положение, первоначально занимаемое пятой светлой полосой. Длина волны света равна 0,5 мкм. Определить толщину пластины [5 мкм]. 1.12.В опыте Юнга расстояние от щелей до экрана равно 3 м. Определить угловое расстояние между светлыми соседними полосами, если третья светлая полоса на экране отстоит от центра интерференционной картины на 4,5 мм. [5·10ˉ4 рад].
Интерференция в плоскопараллельной пластине 1.13.На мыльную пленку с показателем преломления n=1,33 падает по нормали монохроматический свет с длиной волны 0,6 мкм. Отраженный свет в результате интерференции имеет наибольшую яркость. Какова возможная наименьшая толщина пленки? [0,113 мкм]. 1.14.На тонкую пленку в направлении нормали к ее поверхности падает монохроматический свет с длиной волны 500 нм. Отраженный от нее свет максимально усилен вследствие интерференции. Определить минимальную толщину пленки, если показатель преломления материала пленки равен 1,4. [89 нм]. 1.15.На тонкую глицериновую пленку толщиной 1,5 мкм нормально к ее поверхности падает белый свет. Определить число длин волн лучей видимого участка спектра (0,4 ≤ λ ≤ 0,8 мкм), которые будут ослаблены в результате интерференции в проходящем свете. Показатель преломления глицерина равен 1,47. [5]. 1.16.На стеклянную пластинку нанесен тонкий слой прозрачного вещества с показателем преломления n=1,3. Пластинка освещена параллельным пучком монохроматического света с длиной волны 640 нм, падающим на пластинку нормально. Какую минимальную толщину должен иметь слой, чтобы отраженный пучок имел наименьшую яркость? [0,123 мкм]. 1.17.Пучок параллельных лучей с длиной волны 0,6 мкм падает под углом 30˚ на мыльную пленку с показателем преломления n=1,33. При какой возможной наименьшей толщине пленки отраженные лучи будут максимально ослаблены интерференцией? [0,243 мкм]. 1.18.Пучок параллельных лучей с длиной волны 0,6 мкм падает под углом 30˚ на мыльную пленку с показателем преломления n=1,33. При какой возможной наименьшей толщине пленки отраженные лучи будут максимально усилены интерференцией? [0,122 мкм]. 1.19.Пучок белого света падает нормально на стеклянную пластинку, толщина которой равна 0,4 мкм. Показатель преломления стекла равен 1,5. Какие длины волн, лежащие в пределах видимого спектра (0,4 ≤ λ ≤ 0,7 мкм), усиливаются в отраженном пучке? [0,48 мкм]. 1.20.На мыльную пленку с показателем преломления n=1,33 падает белый свет под углом 45˚. При какой наименьшей толщине пленки отраженные лучи будут окрашены в желтый цвет (λ=6.10-7м)? [0,13 мкм]. 1.21.Темной или светлой будет в отраженном свете мыльная пленка толщиной d = 0,1λ? Пленка находится в воздухе, показатель преломления пленки равен 1,3. Считать, что пучок света падает на пленку нормально. [темной]. 1.22.Зимой на стеклах трамваев и автобусов образуются тонкие пленки наледи, окрашивающие все видимое сквозь них в зеленоватый цвет. Оценить, какова наименьшая толщина этих пленок (показатель преломления наледи принять равным 1,33). [~0,5 мкм]. 1.23.На поверхность стеклянного объектива (n1=1,5) нанесена тонкая пленка, показатель преломления которой n2=1,2 («просветляющая» пленка). При какой наименьшей толщине этой пленки произойдет максимальное ослабление отраженного света в средней части видимого спектра? [0,115 мкм]. 1.24.На линзу с показателем преломления n = 1,58 нормально падает монохроматический свет с длиной волны 0,55мкм. Для устранения потерь света в результате отражения на линзу наносится тонкая пленка. Определить: 1) оптимальный показатель преломления для пленки; 2) толщину пленки. [1) 1,26; 2) 109 нм]. 1.25.Тонкая пленка с показателем преломления n=1,5 освещается светом с длиной волны 600 нм. При какой минимальной толщине пленки исчезнут интерференционные полосы? [100 нм]. Интерференция в клине 1.26.На стеклянный клин (n=1,5) с малым углом нормально к его грани падает параллельный пучок лучей монохроматического света с длиной волны 0,698 мкм. Определить угол между поверхностями клина, если расстояние между двумя соседними интерференционными минимумами в отраженном свете равно 2 мм. [ 1.27.На тонкий стеклянный клин (n=1,5) нормально падает монохроматический свет. Угол клина равен 1.28.На стеклянный клин (n=1,5) падает нормально пучок света с длиной волны 0,582 мкм. Угол клина равен 1.29.Между двумя плоскопараллельными стеклянными пластинками (n=1,5) положили очень тонкую проволочку. Проволочка находится на расстоянии 75 мм от линии соприкосновения пластинок и ей параллельна. В отраженном свете с длиной волны 0,5 мкм на верхней пластинке видны интерференционные полосы. Определить толщину проволочки, если на протяжении 30 мм насчитывается 16 светлых полос. [10 мкм]. 1.30.Между двумя плоскопараллельными стеклянными пластинками (n=1,5) на расстоянии 10 см от границы их соприкосновения находится проволока диаметром 0,01 мм, образуя воздушный клин. Пластины освещаются нормально падающим светом с длиной волны 0,6 мкм. Определить ширину интерференционных полос, наблюдаемых в отраженном свете. [3 мм]. 1.31.Монохроматический свет падает нормально на поверхность воздушного клина, причем расстояние между интерференционными полосами равно 0,4 мм. Определить расстояние между интерференционными полосами, если пространство между пластинами, образующими клин, заполнить прозрачной жидкостью с показателем преломления n=1,33. [0,3 мм]. Кольца Ньютона 1.32.Радиус второго темного кольца Ньютона в отраженном свете равен 0,4 мм. Определить радиус кривизны плосковыпуклой линзы, взятой для опыта, если она освещается светом с длиной волны 0,64 мкм. [125 мм]. 1.33.Между стеклянной пластинкой и лежащей на ней плосковыпуклой линзой находится жидкость. Найти показатель преломления жидкости, если радиус третьего темного кольца Ньютона при наблюдении в отраженном свете с длиной волны 0,6 мкм равен 0,82 мм. Радиус кривизны линзы равен 0,5 м. [1,34]. 1.34.На стеклянную пластинку положена выпуклой стороной плосковыпуклая линза. Сверху линза освещена монохроматическим светом длиной волны 500 нм. Найти радиус кривизны линзы, если радиус четвертого темного кольца Ньютона в отраженном свете равен 2 мм. [2 м]. 1.35.Плосковыпуклая стеклянная линза с радиусом кривизны 0,5м лежит выпуклой стороной на стеклянной пластинке. Радиус пятого темного кольца Ньютона в отраженном свете равен 1,1 мм. Определить длину световой волны. [0,484 мкм]. 1.36.Установка для наблюдения колец Ньютона освещается нормально падающим монохроматическим светом с длиной волны 600 нм. Определить толщину воздушного промежутка в том месте, где в отраженном свете наблюдается первое светлое кольцо. [0,15 мкм]. 1.37.Расстояние между вторым и первым тёмными кольцами Ньютона в отраженном свете равно 1 мм. Определить расстояние между десятым и девятым темными кольцами. [0,39 мм]. 1.38.Диаметр второго светлого кольца Ньютона при наблюдении в отраженном свете с длиной волны 0,6 мкм равен 1,2 мм. Определить радиус кривизны плосковыпуклой линзы, взятой для опыта. [0.4м]. 1.39.Плосковыпуклая линза с радиусом кривизны 0,3 м выпуклой стороной лежит на стеклянной пластинке. Радиус четвертого темного кольца Ньютона в проходящем свете равен 0,7 мм. Определить длину световой волны. [0,47 мкм]. 1.40.Плосковыпуклая линза с радиусом кривизны 4 м выпуклой стороной лежит на стеклянной пластинке. Определить длину волны падающего монохроматического света, если радиус пятого светлого кольца в отраженном свете равен 3 мм. [0,5 мкм]. 1.41.Установка для наблюдения колец Ньютона освещается нормально падающим монохроматическим светом с длиной волны 550 нм. Определить толщину воздушного промежутка в том месте, где в отраженном свете наблюдается четвертое темное кольцо. [1,1 мкм]. 1.42.Установка для наблюдения колец Ньютона освещается нормально падающим монохроматическим светом с длиной волны 600 нм. Пространство между линзой и стеклянной пластинкой заполнено жидкостью, и наблюдение ведется в проходящем свете. Радиус кривизны линзы равен 4 м. Определить показатель преломления жидкости, если радиус второго светлого кольца равен 1,8 мм. [1,48]. 1.43.Плосковыпуклая линза выпуклой стороной лежит на стеклянной пластинке. Радиус третьего светлого кольца в проходящем свете с длиной волны 0,6 мкм равен 0,9 мм. Определить радиус кривизны линзы. [0,45 м]. 1.44.Плосковыпуклая линза с радиусом сферической поверхности 12,5 см прижата к стеклянной пластинке. Диаметр десятого темного кольца Ньютона в отраженном свете равен 1 мм. Определите длину волны света. [0,2 мкм]. 1.45.Установка для наблюдения колец Ньютона освещается монохроматическим светом, падающим нормально. При заполнении пространства между линзой и стеклянной пластинкой прозрачной жидкостью радиусы темных колец в отраженном свете уменьшились в 1,21 раза. Определить показатель преломления жидкости. [1,46]. 1.46.Найти радиус центрального темного пятна колец Ньютона, если между линзой и пластинкой налит бензол (n=1,5). Радиус кривизны линзы равен 1 м. Показатели преломления линзы и пластинки одинаковы. Наблюдение ведется в отраженном свете с длиной волны 589 нм. [0,63 мм].
|
|

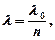
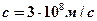 – скорость света в вакууме;
– скорость света в вакууме;  – абсолютный показатель преломления среды, который показывает, во сколько раз скорость света в среде меньше, чем в вакууме;
– абсолютный показатель преломления среды, который показывает, во сколько раз скорость света в среде меньше, чем в вакууме;  – длина волны в вакууме.
– длина волны в вакууме.
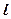 – геометрическая длина пути световой волны в среде с показателем преломления
– геометрическая длина пути световой волны в среде с показателем преломления 
 от оптической разности хода
от оптической разности хода  световых волн:
световых волн:
 – длина световой волны.
– длина световой волны.

 ;
;  ,
, = 0, 1, 2… – номер интерференционной полосы;
= 0, 1, 2… – номер интерференционной полосы;  – расстояние между двумя когерентными источниками, находящимися на расстоянии
– расстояние между двумя когерентными источниками, находящимися на расстоянии  от экрана
от экрана  .
.
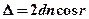 или
или  ,
, или
или  ,
, – угол падения;
– угол падения; 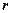 – угол преломления.
– угол преломления.

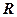 – радиус кривизны линзы.
– радиус кривизны линзы.

 – показатель преломления стекла;
– показатель преломления стекла;  ].
].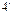 . Определить длину световой волны, если расстояние между двумя соседними интерференционными максимумами в отраженном свете равно 0,2 мм. [698 нм].
. Определить длину световой волны, если расстояние между двумя соседними интерференционными максимумами в отраженном свете равно 0,2 мм. [698 нм]. . Какое число темных интерференционных полос приходится на единицу длины клина? [5 полос на 1 см].
. Какое число темных интерференционных полос приходится на единицу длины клина? [5 полос на 1 см].