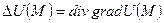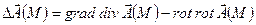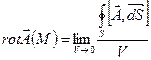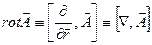|
|
При адиабатическом расширении без совершения внешней работы внутренняя энергия газа не меняется.Для идеального газа это означает Т1 = Т2 (температура не изменяется). Для реального газа Реальный газ при адиабатическом расширении ввакуум охлаждается.
53.Жидкости и их описание. Жидкость является агрегатным состоянием вещества, промежуточным между газообразным и твердым. В газах нет закономерности во взаимном расположении молекул (хаотическое расположение). В твердых телах наблюдается дальний порядок — молекулы образуют кристаллическую решетку. В жидкостях дальний порядок отсутствует, а имеет место ближний порядок в расположении молекул — их упорядоченное расположение повторяется на расстояниях, сравнимых с межатомными. Тепловое движение молекулы в жидкости это ее колебание около определенного положения равновесия в течение некоторого времени, после чего молекула скачком переходит в новое положение, отстоящее от исходного на расстояние порядка межатомного. Радиус г молекулярного действия — расстояние (порядка 10-9 м), при котором можно пренебречь силами притяжения между молекулами жидкости.
Сфера радиусом rназывается сферой молекулярного действия. Силы, действующие на молекулу А внутри объема жидкости со стороны окружающих молекул, в среднем скомпенсированы. Для молекулы В, расположенной на поверхности, равнодействующая сил 54. Поверхностное натяжение. Молекулы поверхностного слоя жидкости обладают большей потенциальной энергией, чем молекулы внутри жидкости. Эта дополнительная энергия, называемая поверхностной энергией, пропорциональна площади поверхности: ΔE = σΔS, где σ—поверхностное натяжение. Так как равновесное состояние характеризуется минимумом потенциальной энергии, то жидкость при отсутствии внешних сил будет принимать такую форму, Поверхностный слой жидкости аналогичен растянутой упругой пленке, в которой действуют силы натяжения. Пусть под действием сил поверхностного натяжения поверхность жидкости стянулась (см. рисунок), при этом силы, действующие на элемент Δl контура, совершают работу ΔA = fΔlΔx, где f— сила поверхностного натяжения, действующая на единицу длины контура поверхности жидкости. Поскольку эта работа совершается за счет уменьшения поверхностной энергии ΔА=ΔЕ, то σ =f, т.е. поверхностное натяжение о равно силе поверхностного натяжения приходящейся на единицу длины контура, ограничивающего поверхность. Единица поверхностного натяжения — ньютон на метр (Н/м) или джоуль на квадратный метр (Дж/м2). 55. Смачивание. Смачиванием называется явление искривления свободной поверхности жидкости при соприкосновении жидкости споверхностью твердого тела. Поверхность жидкости, искривленная на границе с твердым телом, называется мениском. Линия, по которой мениск пересекается ствердым телом, называется периметром смачивания. Явление смачивания характеризуется краевым углом θ между поверхностью твердого тела и мениском в точках их пересечения (в точках периметра смачива Если θ = 0, смачивание считается идеальным (полным). Случай θ = π— это идеальное (полное) несмачивание. Если силы притяжения между молекулами твердого тела и жидкости больше, чем силы притяжения молекул жидкости друг к другу, то жидкость будет смачивающей. Если молекулярное притяжение в жидкости превышает силы притяжения молекул жидкости к молекулам твердого тела, то жидкость не смачивает твердое тело. 56. Давление под искривленной поверхностью жидкости. Сферическая выпуклая поверхность производит на жидкость дополнительное давление, вызванное силами внутреннего натяжения, направленными внутрь жидкости, натяжения направлена из жидкости и давление внутри жидкости Избыточное давление внутри мыльного пузыря радиуса R вызывается действием обоих поверхностных слоев тонкой сферической мыльной пленки:
В общем случае избыточное давление для произвольной поверхности жидкости описывается формулой Лапласа: где R1, и R2 — радиусы кривизны двух любых взаимно перпендикулярных сечений поверхности жидкости в данной точке. Радиус кривизны положителен, если центр кривизны соответствующего сечения находится внутри жидкости, и отрицателен, если центр кривизны находится внежидкости.
57. Капиллярные явления. Капиллярами называются узкие цилиндрические трубки сдиаметром менее миллиметра. Капиллярностью называется явление изменения уровня жидкости в капиллярах. Жидкость в капилляре поднимается или опускается на такую высоту h, при которой давление столба жидкости (гидростатическое давление) ρgh
уравновешивается избыточным давлением Δр: Высота поднятия (глубина опускания) жидкости в капилляре: где ρ— плотность жидкости, r— радиус капилляра, R— радиус кривизны мениска, g—ускорение свободного падения. Высота поднятия (опускания) жидкости в капилляре обратно пропорциональна его радиусу.
58. Кристаллические и аморфные твердые тела. Твердым теломназывается агрегатное состояние вещества, характеризующееся постоянством формы и объема, причем тепловые движения частиц в них представляют собой хаотические колебания частиц относительно положений равновесия. Твердые тела подразделяются на кристаллические и аморфные. Кристаллические тела— это твердые тела, имеющие упорядоченное, периодически повторяющееся расположение частиц. Структура, для которой характерно регулярное расположение частиц с периодической повторяемостью в трех измерениях, называется кристаллической решеткой.
Точки, в которых расположены частицы, а точнее — средние равновесные положения, около которых частицы совершают колебания, называются узлами кристаллической решетки. Характерной особенностью кристаллов является их анизотропность— зависимость физических свойств (упругих, механических, тепловых, электрических, магнитных, оптических) от направления. Анизотропия кристаллов объясняется тем, что плотность расположения частиц по разным направлениям не одинакова. Если кристаллическое тело состоит из единственного кристалла, оно называется монокристаллом.Если твердое тело состоит из множества беспорядочно ориентированных кристаллических зерен, оно называется поликристаллом.В поликристаллах анизотропия наблюдается только для отдельных мелких кристалликов. Твердые тела, физические свойства которых одинаковы по всем направлениям (изотропны), называются аморфными.Для аморфных тел, как и для жидкостей, характерен ближний порядок в расположении частиц, но, в отличие от жидкостей, подвижность частиц в них довольно мала. Органические аморфные тела, молекулы которых состоят из большого числа одинаковых длинных молекулярных цепочек, соединенных химическими связями, называются полимерами (например, каучук, полиэтилен, резина).
59. Типы кристаллов. В зависимости от рода частиц, расположенных в узлах кристаллической решетки, и характера сил взаимодействия между ними кристаллы подразделяются на четыре типа: ионные, атомные, металлические, молекулярные. Ионные кристаллы. В узлах кристаллической решетки располагаются
Атомные кристаллы. В узлах кристаллической решетки располагаются нейтральные атомы, удерживающиеся в узлах решетки ковалентными связями квантово-механического происхождения (у соседних атомов обобществляются валентные электроны, наименее связанные с атомом). Пример атомных кристаллов — алмаз и графит. В алмазе каждый атом углерода связан с четырьмя такими же атомами, которые располагаются на одинаковых расстояниях от него в вершинах тетраэдра. В графите атомы углерода упакованы в плоские слои, связанные между собой слабыми ван-дер-ваальсовыми силами. Металлические кристаллы. В узлах кристаллической решетки располагаются положительные ионы металла. При образовании кристаллической решетки валентные электроны, слабо связанные с атомами, отделяются от атомов и коллективизируются: они уже принадлежат не одному атому, как в случае ионной связи, и не паре соседних атомов, как в случае ковалентной связи, а всему кристаллу в целом. Молекулярные кристаллы. В узлах кристаллической решетки располагаются нейтральные молекулы вещества, силы взаимодействия между которыми обусловлены незначительным взаимным смещением электронов в электронных оболочках атомов. Эти силы называются ван-дер-ваальсовыми, тат как они имеют ту же природу, что и силы притяжения между молекулами, приводящими к отклонению газов от идеальности. Примеры молекулярных кристаллов — органические соединения (например, парафин), инертные газы (Ne, Ar, Кr, Хе) и атмосферные газы СО2, О2, N2 в твердом состоянии, лед, и т.д. 60.Дефекты в кристаллах. Дефектами кристаллической решетки называются отклонения от упорядоченного расположения частиц в узлах решетки. Дефекты делятся на макроскопические, возникающие в процессе образования и роста кристаллов (например, трещины, поры, инородные макроскопические включения), и микроскопические, обусловленные микроскопическими отклонениями от периодичности.
Линейные дефекты нарушают дальний порядок. Особое место среди линейных дефектов занимают дислокации— линейные дефекты, нару-
шающие правильное чередование атомных плоскостей. Различают краевые (край атомной плоскости, обрывающейся в кристалле (а)) и винтовые (атомные плоскости образуют винтовую поверхность (б) дислокации.
61 .Теплоемкость твердых тел.
Рассмотрим идеальную кристаллическую решетку, в узлах которой частицы, принимаемые за материальные точки, колеблются вблизи положений равновесия в трех взаимно перпендикулярных направлениях (три колебательные степени свободы, каждая из которых обладает энергией kТ). Внутренняя энергия моля твердого тела где NA—число Авогадро, R—молярная газовая постоянная. Молярная теплоемкость твердого тела:
Если твердое тело является химическим соединением (например NaCl), то число частиц в моле равно nNA, где п— число атомов в молекуле (для NaCl число частиц в моле равно 2NА, поскольку в одном моле NaCl содержится NА атомов Na и NА атомов Cl). Молярная теплоемкость твердых химических соединений
Отклонения от закона Дюлонга и Пти (особенно при низких температурах) объясняются исходя из квантовых представлений.
62. Изменение агрегатного состояния.
И в жидкостях и в твердых телах всегда есть некоторое число молекул, энергия которых достаточна для преодоления притяжения к другим молекулам, и которые способны покинуть поверхность жидкости или твердого тела. Такой процесс для жидкости называется испарением (или парообразованием), для твердых тел — сублимацией (или возгонкой). Конденсацией называется переход вещества вследствие его охлаждения или сжатия из газообразного состояния в жидкое. Если число молекул, покидающих жидкость за единицу времени через единичную поверхность, равно числу молекул, переходящих из пара в жидкость, то наступает динамическое равновесие между процессами испарения и конденсации. Пар, находящийся в равновесии со своей жидкостью, называется насыщенным. Плавлением называется переход вещества из кристаллического (твердого) состояния в жидкое. Плавление происходит при определенной, В процессе плавления теплота Q, сообщаемая веществу, идет на совершение работы по разрушению кристаллической решетки, и поэтому Tпл =const (рис.(а)) до расплавления всего кристалла. Количество теплоты L, необходимое для расплавления 1кг вещества, называется удельной теплотой плавления. Если жидкость охлаждать, то процесс пойдет в обратном направлении (рис.(б), Q'— количество теплоты, отдаваемое телом при кристаллизации): сначала температура жидкости понижается, затем при постоянной температуре, равной Тпл, начинается кристаллизация. Для кристаллизации вещества необходимо наличие центров кристаллизации — кристаллических зародышей, которыми могут быть как кристаллики образующегося вещества, так и любые инородные включения. Если в чистой жидкости нет центров кристаллизации, то она может быть охлаждена до температуры, меньшей температуры кристаллизации, образуя при этом переохлажденную жидкость (рис.(б) - пунктир). Аморфные тела являются переохлажденными жидкостями.
63.Фазовые переходы. Фазойназывается термодинамически равновесное состояние вещества, отличающееся по физическим свойствам от других возможных равновесных состояний того же вещества. Переход вещества из одной фазы в другую — фазовый переход — всегда связан с качественными изменениями свойств веществ. Фазовый переход первого рода— это переход, сопровождающийся поглощением или выделением теплоты (например, плавление, кристаллизация). Он характеризуется постоянством температуры, изменениями энтропии и объема. Фазовый переход второго рода— переход не связанный с поглощением или выделением теплоты и изменением объема. Он характеризуется постоянством объема и энтропии, но скачкообразным изменением теплоемкости. Фазовые переходы второго рода связаны с изменением симметрии: выше точки перехода система обладает более высокой симметрией, чем ниже точки перехода. Примеры Фазовых переходов второго рода: переход ферромагнитных веществ при определенных давлениях и температуре в парамагнитное состояние; переход металлов и сплавов при низких температурах в сверхпроводящее состояние; превращение обыкновенного жидкого гелия в сверхтекучий. 64.Диаграмма состояния. Если система является однокомпонентной, т.е. состоящей из химически однородного вещества или его соединения, то понятие фазы совпадает с понятием агрегатного состояния.
Кривые на диаграмме называются кривыми фазового равновесия, каждая точка на них соответствует условиям равновесия двух сосуществующих фаз. Тройной точкойназывается точка, в которой пересекаются кривые фазового равновесия и которая, следовательно, определяет условия (температуру Ттри давление ртр) одновременного равновесного сосуществования трех фаз вещества. Тройная точка воды соответствует температуре 273,16 К (или 0,01°С по шкале Цельсия) и является основной реперной точкой для построения термодинамической температурной шкалы.
65.Уравнение Клапейрона-Клаузиуса Уравнение Клапейрона-Клаузиуса: Здесь L— теплота фазового перехода (например, в случае плавления — удельная теплота плавления), (V2 — V1)— изменение объема вещества при переходе его из первой фазы во вторую, Т— температура перехода (например, в случае плавления — температура плавления Гпл). Поскольку L и Т всегда положительны, то наклон кривой равновесия определяется знаком (V2 — V1). Так при испарении и сублимации объем всегдавозрастает, поэтому dp/dT>0. При плавлении у большинства веществ объем возрастает, следовательно dp/dT > 0, т.е. увеличение давления приводит к повышению температуры плавления (сплошная КП на рисунке). Для некоторых веществ (вода, Ge, чугун) объем жидкой фазы меньше объема твердой фазы, т.е. dp/dT<0; следовательно, увеличение давления сопровождается понижением температуры плавления (штриховая линия на рисунке).
66.Анализ диаграммы состояния. Диаграмма состояния, позволяет судить, в каком состоянии находится данное вещество при определенных р и Т, а также какие фазовые переходы будут происходить в том или ином процессе.
При изобарном нагреве 4-5-6 в точке 5 начинается плавление, 6— кипение. При изобарном нагреве 7-8 твердое тело превращается в газ, минуя жидкую фазу. При изотермическом сжатии 9-10 вещество пройдет три состояния: газ-жидкость-кристалл. Кривая испарения заканчивается критической точкой (К). Поэтому возможен непрерывный переход вещества из жидкого состояния в газообразное и обратно в обход критической точки, без пересечения кривой испарения (переход 11-12), т.е. такой переход, который не сопровождается фазовыми превращениями. Это возможно потому, что различие между газом и жидкостью является чисто количественным (оба эти состояния, например, являются изотропными). Переход же кристаллического состояния в жидкое или газообразное может быть только скачкообразным (в результате фазового перехода), поэтому кривые плавления и сублимации не могут обрываться, как это имеет место для кривой испарения в критической точке. Кривая плавления уходит в бесконечность, а кривая сублимации идет в точку, где р=0 и Т=0.
ПРИЛОЖЕНИЕ Основные понятия математического аппарата физики. 1.Понятие производной функции. Функция f называется дифференцируемой в точке
Этот предел называется производной функции f в точке
2.Производные некоторых элементарных функций.
3. Частная производная. Пусть функция f определена в некоторой окрестности точки
этот предел называется частной производной функции f (по 4.Полный дифференциал функции f в точке
5.Определенный интеграл. Пусть функция f(x) определена и ограничена на отрезке [a,b]. Разобьем этот отрезок на "элементарные" отрезки введением и точек Обозначим через dx длину элементарного отрезка Число Функция f(x) называется интегрируемой на отрезке [a,b], если существует число I со следующим свойством: для любого ε>0 найдется такое δ(ε)>0, что при любом разбиении на отрезки dx, для которого dx<δ , выполняется неравенствo Число I называется определенным интегралом функции f(x) на отрезке [а,b] и обозначается: 6.Вектор. Геометрический вектор В прямоугольной декартовой системе координат каждый вектор 7. Скалярное произведение векторов.
Скалярное произведение векторов
где φ - угол между векторами 8. Векторное произведение векторов.
Под векторным произведением векторов Обозначение: 9.Скалярное поле. Если каждой точке М пространства ставится в соответствие скалярная величина U, то возникает скалярное поле U(M) (например, поле температуры неравномерно нагретого тела, поле плотности в неоднородной среде, поле электростатического потенциала). Если М имеет декартовы координаты (x,y,z), то пишут U = U(x,y,z) или 10. Векторное поле Если каждой точке М ставится в соответствие вектор
где 11.Производная по направлению. Пусть скалярное поле Значение этой производной существенно зависитот выбора направления 12.Градиент. Градиентом поля Тогда Часто вектор gradU обозначают также
13.Поток поля через поверхность. Разобьем данную поверхность S на n элементарных площадок размером 1) Поток скалярного поля: 2) Скалярный поток векторного поля: 3) Векторный поток векторного поля: 14.Производная по объему. Под производными по объему скалярного или векторного полей в точке М понимают величины трех типов, которые получают следующим образом. (1) Точка М окружается замкнутой поверхностью S, которая охватывает область с объемом V. (2) Вычисляется интеграл
отношения этого интеграла к объему V, когда S стягивается в точку М, так что V стремится к нулю. 15. Дивергенция векторного поля. Дивергенцией(обозначается
Величина Дивергенция Для пространственной области G, ограниченной замкнутой поверхностью S:
17.Оператор Лапласа. Пусть U(M) — скалярное поле, тогда оператор Лапласа
или в декартовых координатах:
Оператор Лапласа векторного поля: 18.Ротор векторного поля. Ротором (вихрем) векторного поля
Обозначается: 19.Теорема Стокса. Циркуляция векторного поля
Примечание. В этом приложении приведены определения некоторых математических понятий, часто используемых в курсе физики. Материал носит справочный характер, поскольку предполагается, что данные понятия известны читателю.
ГРЕЧЕСКИЙ АЛФАВИТ |
|
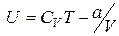 , поэтому
, поэтому 
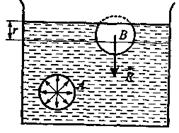
 направлена внутрь жидкости. Результирующие силы всех молекул поверхностного слоя оказывают на жидкость молекулярное (внутреннее) давление.
направлена внутрь жидкости. Результирующие силы всех молекул поверхностного слоя оказывают на жидкость молекулярное (внутреннее) давление. чтобы при заданном объеме она имела минимальную поверхность, т.е. форму шара.
чтобы при заданном объеме она имела минимальную поверхность, т.е. форму шара. ния). Жидкость называется смачивающей твердое тело, если краевой угол острый: 0≤θ<π/2 (рис.а) и несмачивающей, если π/2< θ < π (рис.б).
ния). Жидкость называется смачивающей твердое тело, если краевой угол острый: 0≤θ<π/2 (рис.а) и несмачивающей, если π/2< θ < π (рис.б).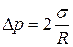 , где R— радиус сферы. Если поверхность жидкости вогнутая, то результирующая сила поверхностного
, где R— радиус сферы. Если поверхность жидкости вогнутая, то результирующая сила поверхностного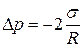 .
.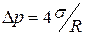 .
.
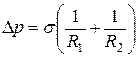

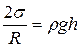
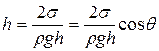
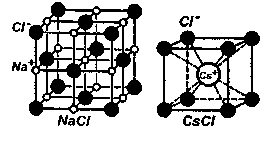 поочередно ионы противоположного знака. Структуры решеток двух наиболее характерных ионных кристаллов — NaCl (решетка представляет собой две одинаковые гранецентрированные кубические решетки, вложенные друг в друга; в узлах одной из этих решеток находятся ионы Na+, в узлах другой — ионы Сl-) и CsCl (кубическая объемно-центрированая решетка — в центре каждой элементарной ячейки находится ион) — показаны на рисунке. Связь, обусловленная кулоновскими силами притяжения между разноименно заряженными ионами называется ионной.
поочередно ионы противоположного знака. Структуры решеток двух наиболее характерных ионных кристаллов — NaCl (решетка представляет собой две одинаковые гранецентрированные кубические решетки, вложенные друг в друга; в узлах одной из этих решеток находятся ионы Na+, в узлах другой — ионы Сl-) и CsCl (кубическая объемно-центрированая решетка — в центре каждой элементарной ячейки находится ион) — показаны на рисунке. Связь, обусловленная кулоновскими силами притяжения между разноименно заряженными ионами называется ионной.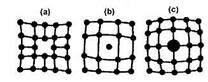 Микродефекты делятся на точечные и линейные. Точечные дефекты бывают трех типов: 1) вакансия— отсутствие атома в узле кристаллической решетки (а); 2) междоузельный атом — атом, внедрившийся в междоузельное пространство (b); 3) примесный атом— атом примеси, либо замещающий атом основного вещества в кристаллической решетке (примесь замещения (с)), либо внедрившийся в междоузельное пространство (примесь внедрения). Точечные дефекты нарушают только ближний порядок в кристаллах.
Микродефекты делятся на точечные и линейные. Точечные дефекты бывают трех типов: 1) вакансия— отсутствие атома в узле кристаллической решетки (а); 2) междоузельный атом — атом, внедрившийся в междоузельное пространство (b); 3) примесный атом— атом примеси, либо замещающий атом основного вещества в кристаллической решетке (примесь замещения (с)), либо внедрившийся в междоузельное пространство (примесь внедрения). Точечные дефекты нарушают только ближний порядок в кристаллах.
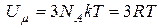
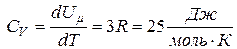 — закон Дюлонга и Пти — молярная теплоемкость химически простых тел в кристаллическом состоянии одинакова (равна 3R) и не зависит от температуры.
— закон Дюлонга и Пти — молярная теплоемкость химически простых тел в кристаллическом состоянии одинакова (равна 3R) и не зависит от температуры.
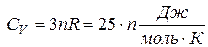
 т.е. равна сумме атомных теплоемкостей элементов, составляющих это соединения.
т.е. равна сумме атомных теплоемкостей элементов, составляющих это соединения.
 возрастающей с увеличением внешнего давления, температуре плавления Tпл.
возрастающей с увеличением внешнего давления, температуре плавления Tпл. Для наглядного изображения фазовых
Для наглядного изображения фазовых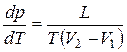 позволяет определить наклоны кривых равновесия.
позволяет определить наклоны кривых равновесия.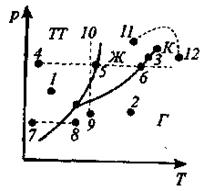 Например, при условиях, обозначенных: точкой 1 вещество — в твердом состоянии (TТ), 2— в газообразном (Г). 3— одновременно в жидком (Ж) и газообразном.
Например, при условиях, обозначенных: точкой 1 вещество — в твердом состоянии (TТ), 2— в газообразном (Г). 3— одновременно в жидком (Ж) и газообразном. , если существует предел разностного отношения функции f в точке
, если существует предел разностного отношения функции f в точке 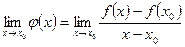

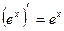
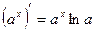
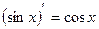
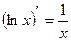
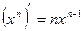

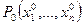 . Функция f называется дифференцируемой по
. Функция f называется дифференцируемой по  , если существует предел разностного отношения
, если существует предел разностного отношения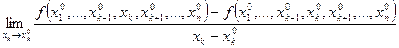
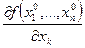 или
или 
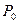 :
:
 - следующим образом:
- следующим образом: 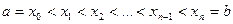
 . В каждом элементарном отрезке выберем произвольное число
. В каждом элементарном отрезке выберем произвольное число 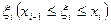 .
.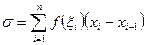 называется интегральной суммой.
называется интегральной суммой. независимо от выбора
независимо от выбора 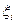 .
.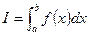 . Здесь х называется переменной интегрирования, a и b — соответственно нижним и верхним пределами интегрирования.
. Здесь х называется переменной интегрирования, a и b — соответственно нижним и верхним пределами интегрирования.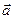 — это направленный отрезок в пространстве. Длина вектора
— это направленный отрезок в пространстве. Длина вектора 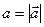 .
.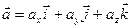 , где i,j,k — единичные векторы (орты) по осям координат x,y,z. Числа
, где i,j,k — единичные векторы (орты) по осям координат x,y,z. Числа  называются прямоугольными декартовыми координатами вектора
называются прямоугольными декартовыми координатами вектора 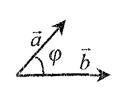
 есть число
есть число 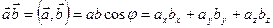

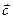 , имеющий длину
, имеющий длину 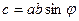 (площадь параллелограмма, построенного на
(площадь параллелограмма, построенного на 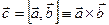 .
. с векторным аргументом (радиусом вектором)
с векторным аргументом (радиусом вектором) 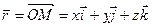 .
. , то говорят о векторном поле
, то говорят о векторном поле 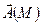 (например, поле скоростей движущейся жидкости, гравитационное поле Солнца, поле электрической напряженности, поле магнитной напряженности). В декартовых координатах:
(например, поле скоростей движущейся жидкости, гравитационное поле Солнца, поле электрической напряженности, поле магнитной напряженности). В декартовых координатах: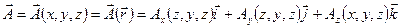
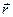 - радиус-вектор. Компоненты Ax,Ay,Az образуют три скалярных поля и однозначно определяют
- радиус-вектор. Компоненты Ax,Ay,Az образуют три скалярных поля и однозначно определяют 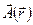 — векторную функцию векторного аргумента.
— векторную функцию векторного аргумента.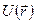 имеет в некоторой точке М0 значение U0, и пусть при перемещении
имеет в некоторой точке М0 значение U0, и пусть при перемещении 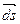 по направлению вектора
по направлению вектора 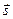 мы приходим из точки М0 в точку М, где скалярное поле имеет значение Us. Приращение U при этом перемещении равно
мы приходим из точки М0 в точку М, где скалярное поле имеет значение Us. Приращение U при этом перемещении равно 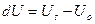 . Предел отношения этого приращения dU к численной величине перемещения ds называется производной скаляра U в точке М0 по направлению
. Предел отношения этого приращения dU к численной величине перемещения ds называется производной скаляра U в точке М0 по направлению 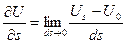

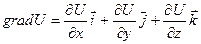
 , где
, где 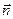 - единичный вектор в направлении
- единичный вектор в направлении 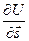 или
или  , где
, где 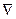 ("набла") обозначает символический вектор, называемый оператором Гамильтона или набла-оператором:
("набла") обозначает символический вектор, называемый оператором Гамильтона или набла-оператором: 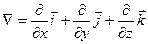
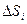 . Внутри каждой площадки выберем точку
. Внутри каждой площадки выберем точку  - и в этой точке построим нормальный к поверхности единичный вектор
- и в этой точке построим нормальный к поверхности единичный вектор  направление которого
направление которого 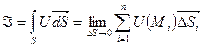
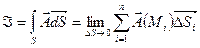

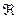 по поверхности S:
по поверхности S:
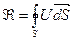 , или
, или 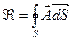 , или
, или 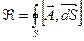 . (3) Определяется предел
. (3) Определяется предел 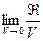
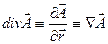 ) векторного поля
) векторного поля 
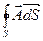 есть скалярный поток векторного полячерез замкнутую поверхность S, которая окружает точку М и охватывает область G с объемом V.
есть скалярный поток векторного полячерез замкнутую поверхность S, которая окружает точку М и охватывает область G с объемом V.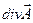 есть мера источников поля
есть мера источников поля 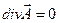 , то векторное поле
, то векторное поле 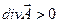 принято называть источникамиполя, а те, в которых
принято называть источникамиполя, а те, в которых 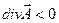 — стокамиполя. 16.Формула Гаусса-Остроградского.
— стокамиполя. 16.Формула Гаусса-Остроградского.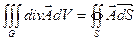
 определяется следующим образом:
определяется следующим образом: