|
|
Методические указания к изучению отдельных темКафедра физической, коллоидной химии и управления качеством
ХИМИЯ, часть 2
Методические указания к изучению дисциплины и выполнению контрольной работы для студентов всех форм обучения и МИППС направления 20.03.01– Техносферная безопасность
Составитель: канд. хим. наук, доцент Л.В. Боровская
УДК 541.13(07)
Химия. Часть 2. Методические указания к изучению дисциплины и выполнению контрольной работы для студентов всех форм обучения и МИППС направления 20.03.01– Техносферная безопасность. / Сост. Л.В. Боровская. ФБГОУ Кубан. гос.технол. ун-т. Кафедра физической, коллоидной химии и управления качеством.– Краснодар: 2015 –56 с. Режим доступа: http://moodle.kubstu.ru (по паролю)
Содержит теорию, вопросы для самопроверки, вопросы и задачи для выполнения контрольной работы с примерами решения по дисциплине "Химия, часть 2" направления 20.03.01– Техносферная безопасность. Указана методическая литература, рекомендуемая для самостоятельного выполнения контрольной работы.
Методические указания к изучению отдельных тем
1.1. ТЕМА 1: ОСНОВЫ ХИМИЧЕСКОЙ ТЕРМОДИНАМИКИ Термодинамический метод является одним из самых мощных методов физической химии. Он дает точные соотношения между энергией и свойствами системы, не требуя каких-либо сведений о строении молекул или механизме процессов. Термодинамика применяется к системам, находящимся в равновесии, и рассматривает только начальные и конечные состояния Она не описывает протекания процессов во времени, она только отвечает на вопрос, насколько глубоко должна пройти данная реакция, прежде чем будет достигнуто равновесие. Приступая к изучению законов химической термодинамики, усвойте основные понятия и определения, которыми она пользуется. К таким понятиям относятся термодинамическая, открытая и закрытая, изолированная, гомогенная, одно- и многокомпонентная системы. Интенсивные свойства системы, которые количественно независимы от объема и массы системы, принято называть термодинамическими параметрами состояния. Когда система под влиянием различных воздействий переходит от начального равновесного состояния к конечному, изменение любого ее свойства не зависит от пути процесса. Бесконечно малое изменение любого свойства — это полный дифференциал, интеграл от которого не зависит от пути интегрирования. Так как теплота и работа являются формами передачи энергии между внешней средой и системой и относятся к определенному процессу, они не могут быть функциями состояния системы. Бесконечно малое количество теплоты и работы обозначают dQ и dW. Для бесконечно малого изменения состояния системы математическое выражение первого закона термодинамики примет вид dQ = dU+dW = dU+pdv+dW`, где dW — сумма всех элементарных работ, равная работе преодоления внешнего давления pdV и прочих сил, а dW` (так называемая полезная работа). Теплота, получаемая системой, считается положительной, а отданная — отрицательной. Необходимо усвоить разницу понятий «теплота процесса» и «тепловой эффект процесса». Теплота процесса — это количество теплоты, выделенной и поглощенной в любом процессе. Тепловой эффект процесса·—это количество теплоты, которая поглощается или выделяется в процессе, протекающем термодинамически необратимо при постоянном объеме или давлении, если к тому же температура исходных веществ и продуктов реакции одинаковая и полезная работа равна нулю. Для понимания всех термодинамических расчетов, с которыми на протяжении курса придется встречаться, следует знать, какие процессы называют обратимыми и какие — необратимыми. Во всяком обратимом процессе равновесная система проходит через последовательный ряд равновесных состояний. Поэтому в таком процессе осуществляется максимальная работа, если она производится системой над внешней средой, и минимальная — в обратном случае. Отсюда вытекают характерные особенности обратимого процесса: его двусторонность, отли-чие внешних сил от внутренних на бесконечно малую величину, малое различие температуры равновесной системы и внешней среды при протекании неизотермического процесса, бесконечно медленное протекание процесса, отсутствие расхода энергии на разные потери. Каким бы путем система ни вернулась в исходное состояние, ее свойства останутся неизменными, и только в обратимом процессе допускается возможность возвращения системы в первоначальное состояние без каких-либо изменении не только в самой системе, но и во внешней среде. В обратимом процессе в каждый момент состояния системы известны все ее параметры, поэтому имеется возможность, исходя из уравнения состояния, выразить любой параметр системы через другие параметры, что крайне необходимо при интегрировании дифференциальных уравнений для расчета изменения свойств системы. Полученные уравнения позволяют рассчитать изменения свойств при необходимом процессе, если он проте-кает от одного и того же начального к одному и тому же конечному состоянию. Чтобы понять, что происходит в системе при изменении температуры и давления, необходимо знать, что внутренняя энергия системы склады-вается из кинетической энергии молекулярного движения, из энергии взаимного притяжения и отталкивания частиц, составляющих систему, из химической внутримолекулярной энергии, энергии электронного возбуждения, внутриядерной энергии, лучистой энергии и гравитационной энергии, обусловленной тяготением частиц друг к другу. В отличие от первого закона термодинамики второй закон применим к явлениям, представляющим собой результат действия большого числа частиц, т.е. к явлениям, к которым применимы законы вероятности. Статистическая природа второго закона позволяет определять наиболее вероятный путь процесса. Наряду с другими формулировками второго закона термодинамики, которые носят частный характер, обращаем внимание на формулировку, согласно которой за счет любого самопроизвольного процесса можно получить работу. Если при этом процесс будет протекать термодинамически обратимо, то работа будет максимальной, определяющей движущую силу процесса. Исходя из основного уравнения второго начала термодинамики
надо уметь показать, что: 1) только в изолированной системе энтропия как функция состояния определяет направленность процессов и состояние равновесия независимо от характера процесса; 2) в неизолированных системах при соответствующих условиях направленность процессов, их состояние равновесия и движущая сила процесса определяются с помощью термодинамических потенциалов: А — энергия Гельмгольца (изохорно-изотермический потенциал при V, Т — const), G — энергия Гиббса (изобарно-изотермический потенциал при ρ и Т — const), U —внутренняя энергии (изохорно-изоэнтропийный потенциал, V и S—const), Η — энтальпия (изобарно-изоэнтропийный потенциал, ρ и S—const). Все термодинамические потенциалы являются свойствами системы при любых условиях, но направленность процессов они определяют только при постоянстве соответствующих двух параметров. Для практических расчетов пользуются абсолютными значениями энтропии в стандартном состоянии, вычисленными при помощи постулата Планка (энтропия чистых твердых веществ, образующих идеальные кристаллы, при абсолютном пуле равна нулю) и сведенными в таблицы. В справочниках, как правило, энтропия дастся при 298 К и обозначается Стандартным состоянием вещества называют состояние, в котором это вещество находится под давлением 1,0133*105 Па. От этих значений энтропии легко перейти к абсолютным значениям при любой температуре. Стандартное значение энтропии при температуре Т обозначается Другие термодинамические функции приводят в виде изменения В курсе физической химии приходится часто встречаться с понятием «химический потенциал», введенным в термодинамику Гиббсом. Химический потенциал какого-либо компонента в смеси равен частной производной термодинамического потенциала системы по количеству молей данного вещества:
В каждом отдельном случае частная производная берется при постоянстве тех параметров, при которых термодинамический потенциал определяет направленность процесса, а также при постоянстве числа молей в системе всех веществ, кроме того вещества, для которого определяется химический потенциал. Таким образом, химический потенциал показывает, насколько изменится термодинамический потенциал системы при соответствующих условиях, если в бесконечно большой объем се прибавить 1 моль данного вещества. Подобно тому, как температура является движущей силой при теплопередаче, химический потенциал — движущая сила, определяющая переход массы. Отсюда следует, что если данный компонент присутствует в равновесной системе в нескольких сосуществующих фазах, то значение его химического потенциала будет одинаковым в каждой фазе. Вопросы для самопроверки к теме 1: 1. Какие формулировки 1–го закона термодинамики Вы знаете приведите их математическую запись. 2. Энергия системы (работа и теплота). Qp, Qv и связь DH с DU (на примере реакций CO2+MgO=MgCO3, NaOH+HCl=NaCl+H2O при температуре 90оС). 3. Как читается закон Гесса и для каких целей применяются следствия из закона? Примените закон для расчета тепловых эффектов Qp и Qv реакций (на примере реакции горения бензола и образования нитробензола или реакции CaC03=CaO+CO2). 4. Что такое теплота образования и сгорания, калорийность пищи (на примере фруктозы С6Н12О6 или глюкозы С12Н22О11)? 5. Как звучат формулировки 2–го закона термодинамики, приведите их математическую запись. 6. Покажите, при каких условиях энтропия может служить как критерий направленности процесса (на примере реакции S+O2=SO2). 7. Почему энергия Гиббса и энергия Гельмгольца могут выступать как критерии направленности самопроизвольного процесса?Напишите соотношение между DF и DG (на примере реакции MgCO3=MgO+CO2).
1.2 ТЕМА 2: ХИМИЧЕСКОЕ РАВНОВЕСИЕ Учение о химическом равновесии является одним из основных разделов курса физической химии. В нем на основе первого и второго законов термодинамики, имеющих общий характер, а также тепловой теоремы Нернста и постулата Планка, называемых третьим законом термодинамики, решаются вопросы, связанные с расчетом химического равновесия, устойчивости веществ и направленности процесса. А также выясняются оптимальные условия режима в процессе химического превращения, позволяющие добиться максимального выхода желаемых веществ. Необходимо знать как, не прибегая к исследованию химического превращения, связанного с затратой больших средств, на основании термических и термохимических данных для исходных веществ и продуктов реакции теоретически предсказать возможность осуществления данного процесса и произвести расчеты выходов при различных условиях его протекания. Вот почему усвоить этот раздел — значит не только осмысленно выводить уравнения изотермы, изохоры, изобары химической реакции, понять сущность третьего закона термодинамики, но и уметь производить расчеты констант химического равновесия, выраженных различным образом, расчеты выходов продуктов реакций при различных условиях опыта, тепловых эффектов реакции на основании экспериментальных данных по изучению равновесного состояния реакции. Только при этих условиях можно научиться решать кардинальные вопросы синтеза новых веществ и интенсификации существующих производств.
Вопросы для самопроверки к теме 2: 1. Химическое равновесие, константа равновесия Кр, Кс, КN, принцип Ле-Шателье (на примере реакции Н2О2=Н2+О2 при температуре 300 К). 2. Уравнение изотермы химической реакции. Связь между Кp, Кc , КN (на примере реакции СО+1/2О2=СО2). 3. Как влияет понижение давления на равновесие в реакции 2С12+2Н20(г)= 4НС1+02, если все вещества находятся в идеальном газообразном состоянии? 4. Как записать выражение константы равновесия для следующей реакции: 1/З А(г)+1/4 В(г) =1/5 С(т)+ 1/7D(г) ? 5. Для реакции H2+1/202 =H2O при 298 К Кр=З,41*1037 Па-1/2. В какую сторону смещено равновесие при 298 К в стандартных условиях? 6. Как влияет повышение давления на равновесие в реакции 2С12 + 2Н20(г)= 4НС1+O2, если все вещества находятся в идеальном газообразном состоянии? 7. Как влияет повышение температуры на равновесие эндотермической реакции 2С12 + 2Н20(г)= 4НС1+O2, если все вещества находятся в идеальном газообразном состоянии?
1.3 ТЕМА 3: ФАЗОВОЕ РАВНОВЕСИЕ И УЧЕНИЕ О РАСТВОРАХ Ознакомившись с сущностью физико-химического анализа, его значением, освоившись с понятиями «фаза», «компонент», «степени свободы», обратите внимание на следующее. Фаза не является понятием, адекватным понятию агрегатного состояния. В однокомпонентных системах могут находиться в равновесном состоянии две фазы одинакового агрегатного состояния серы, например, моноклинная, ромбическая. В тех случаях, когда число компонентов в системе меньше числа веществ, выбор веществ в качестве компонентов произволен. Когда же в равновесной системе имеются две фазы с тождественным составом, то независимо от числа веществ система будет вести себя как однокомпонентная. Так, азеотропная смесь, состоящая из любого числа веществ,— система однокомпонентная, так как состав пара и жидкости одинаковый. Такой вывод является следствием из правила фаз Гиббса, а не эмпирическим правилом. Число степеней свободы определяется числом компонентов и фаз, находящихся в равновесной системе. Оно может быть равным нулю, единице, двум, трем и т. д. Необходимо в каждом отдельном случае умегь сделать практические выводы в зависимости от числа степеней свободы, помня, что выбор параметра в качестве степени свободы произволен. Следует пользоваться правилом фаз при изучении однокомпонентных (диаграммы состояния воды, серы), двухкомпонентных и простейших трехкомпонентных систем (жидкие смеси, сплавы и растворы твердых веществ в жидких растворителях) На изучении опытных данных диаграмм состав — давление, состав — температура кипения бинарных безгранично смешивающихся жидких смесей основаны два закона Коновалова и три закона Вревского, а на изучении двух- и трехкомпонентных систем — правило рычага. Изучая перегонку смесей, уясните, что различные виды перегонки (перегонка в равновесии, простая перегонка и ректификация) основаны на различии состава пара и жидкости. Необходимо приобрести навыки чтения диаграмм состав·—свойство различных бинарных жидких смесей, диаграмм плавкости и простейших диаграмм трехкомпонентных систем Чтение диаграммы заключается в безошибочном определении в любой точке на диаграмме числа компонентов, степеней свободы, фаз их состава и массового соотно-шения, а также в определении температур начала и конца кристаллизации, плавления, кипения и конденсации. Надо знать, на основании каких экспериментальных данных строятся различные диаграммы Для разбавленных растворов нелетучих веществ изучаются: · осмотическое давление · понижение давления пара растворителя над раствором · понижение температуры замерзания раствора · повышение температуры кипения раствора. Надо уметь показать взаимосвязь между этими свойствами, знать термодинамический вывод закона Рауля, уравнений для расчета понижения температуры замерзания и повышения температуры кипения раствора, уравнений для расчета криоскопической и эбуллиоскопической постоянных. Выводы уравнений будут более осмысленны, если вы поймете, что жидкость закипает, когда давление пара над раствором становится равным внешнему давлению, а замерзание, т. е. появление первых кристаллов твердой фазы, происходит, когда давление насыщенных паров над твердой фазой и жидкостью будет одинаковым. Во всех уравнениях, выражающих связь между концентрацией идеального· раствора и каждым его свойством, значение свойства не зависит от природы растворителя (осмотическое давление, относительное понижение давления пара) или не зависит от природы растворенного вещества (изменение температур замерзания и кипения растворов), а определяется только числом частиц растворенного вещества. Это обстоятельство послужило основанием для физической теории растворов и позволило понять свойства разбавленных растворов электролитов, в уравнения расчета которых вводится изотонический коэффициент Вант-Гоффа, учитывающий увеличение числа частиц вследствие диссоциации. Необходимо освоить химическую теорию растворов, в развитии которой большая роль принадлежит Д И. Менделееву. На положениях этой теории основаны современные представления о процессах растворения, при этом всегда учитывается влияние полярности молекул растворителя на растворимость данного вещества. Следует различать понятия дифференциальной и интегральной теплоты растворения и разбавления.
Вопросы для самопроверки к теме 3: 1. Объясните, что такое фазовое равновесие, раскройте правило фаз Гиббса, приведите диаграмму состояния в координатах Р,Т для однокомпонентных систем на примере воды. 2.Какие фазовые переходы Вы знаете? Для каких систем применяется уравнение Клапейрона – Клаузиуса, дайте его анализ (на примере воды и аммиака). 3.Как определяются тепловые эффекты фазовых переходов? 4. Каковы границы применимости закона Рауля ? (Покажите на примере водного раствора сахара). Положительные и отрицательные отклонения от закона. 5. Что такое криоскопия и эбулиоскопия растворов? Одинаковы ли температуры повышения кипения раствора у электролитов и неэлектролитов? Влияет ли природа растворителя и растворенного вещества на понижение температуры замерзания и повышения температуры кипения раствора (на примере водных растворов глицерина и хлорида кальция)? Использование этих явлений в технологии. 7. Что такое коэффициент распределения в трехкомпонентной системе? Метод определения коэффициента распределения и установление факта диссоциации и ассоциации в системе (на примере системы вода+NaCl+растительное масло).
1.4. ТЕМА 4: ЭЛЕКТРОХИМИЯ Электрохимия занимается изучением закономерностей, связанных с взаимным превращением химической и электрохимической форм энергии. Химические реакции сопровождаются обычно поглощением или выделением теплоты — тепловым эффектом реакции, а не электрической энергии. В электрохимии рассматриваются реакции или протекающие за счет подведенной извне электрохимической энергии, или служащие источником ее получения. Такие реакции называются электрохимическими. Очевидно, что электрохимические реакции с термодинамической точки зрения не идентичны химическим, поэтому электрохимия должна рассматриваться как самостоятельный раздел физической химии, выделившийся в самостоятельную науку. Чтобы понять процесс образования ионов в растворе, обратите внимание на величину энергии гидратации, сопоставив ее с величинами тепловых эффектов реакций. Изучая удельную и эквивалентную электрические проводимости, влияние различных факторов на их значение, уясните, что величину удельной и эквивалентной электрической проводимости различных электролитов определяют валентность ионов, их абсолютная скорость и число ионов в единице объема (в случае удельной электрической проводимости) и в объеме, содержащем килограмм-эквивалент массы (в случае эквивалентной электрической проводимости). Тοгда станет понятным влияние на удельную и эквивалентную электрическую проводимость размера иона (кристаллографического радиуса), степени сольватации, природы растворителя, температуры, концентрации электролита и неэлектролита, вязкости раствора и, особенно в случае сильных электролитов, наличия электростатического взаимодействия между ионами, приводящего к образованию ионных атмосфер. Переходя к изучению свойств сильных электролитов, необходимо знать, какие экспериментальные данные явились основанием для появления теории сильных электролитов. Рассматривая основные положения электростатистической теории сильных электролитов по Дебаю и Гюккелю, обратите внимание на неточности, допущенные при расчете коэффициента активности соли и ионов, которые привели к тому, что полученные уравнения для расчета коэффициента активности применимы только к разбавленным растворам. При изучении гальванических элементов обратив внимание на то, что скачок потенциала всегда возникает при соприкосновении двух проводников одного и того же или разного рода. Выясните, какие факторы определяют значение потенциалов. Уясните разницу между понятиями «потенциал на границе металл — раствор» и «электродный потенциал». Необходимо ознакомиться с принятой классификацией электродов (первого, второго рода и редокс-электроды) и различными типами гальванических элементов. Выводу уравнения Нернста для расчетов электродных потенциалов и ЭДС любого гальванического элемента должна предшествовать запись уравнения протекающего в нем процесса. В концентрационных элементах ток возникает за счет выравнивания концентрации ионов или вещества электрода, а в химических элементах — за счет химической реакции. Необходимо знать метод и схему измерения электрической проводимости и ЭДС гальванических элементов, а также применение кондуктометрического метода для титрования окрашенных растворов, определения константы диссоциации, произведения растворимости, энергии Гиббса и теплоты диссоциации; применение потенциометрии для определения рН растворов, активности ионов растворов; определение изменения термодинамических параметров химической реакции.
Вопросы для самопроверки к теме 4:
1. Что такое удельная и эквивалентная электропроводность? Законы Кольрауша, границы их применимости (на примере растворов соляной и муравьиной кислот). Абсолютные скорости движения ионов и их подвижность; причина аномальных значений подвижности ионов Н+ и ОН–. 2. Какова связь между константой диссоциации и эквивалентной электропроводностью (уравнение Оствальда)? на примере реакции диссоциации муравьиной кислоты. 3. Что такое кондуктометрическое титрование (на примере титрование смеси, содержащей а)CH3CH2COOH+HCl; б) H2SO4 + HCl или технического раствора, содержащего одновременно CuSO4 и HCl)? Объяснение кривых титрования. 4. Как работает гальванический элемент? Устройство, условная запись, уравнение Нернста для расчета электродного потенциала и ЭДС (на любом примере). 5. Что такое условные электродные потенциалы (на примере свинцового электрода)? Ряд напряжений. 6. Что такое электроды первого и второго рода, окислительно-восстановительные, примеры (устройство, условная запись, уравнение Нернста для расчета их электродного потенциала)? 7. Индикаторные электроды: устройство, условная запись, уравнение Нернста для расчета их электродного потенциала (на примере определения концентрации Н+ 0,1н раствора соляной кислоты). 8. Хлорсеребряный и водородный электроды - как электроды сравнения, использование их, уравнение Нернста для них. 9. Какие экспериментальные данные нужны для определения основных термодинамических свойств методом ЭДС (на примере элемента, в котором протекает реакция Cu+ CrSO4
1.5. ТЕМА 5: ХИМИЧЕСКАЯ КИНЕТИКА И КАТАЛИЗ Химическая кинетика — это учение о химическом процессе, его механизме и закономерностях протекания во времени. Изучение материала этого раздела позволяет более успешно решать вопросы интенсификации производства. Рекомендуем после ознакомления с основными понятиями (механизм, скорость реакции, молекулярность и порядок реакции, константа скорости химической реакции) и классификацией химических реакций перейти к изучению основных положений, теорий химической кинетики (теория Аррениуса, теория активных столкновений, теория переходного состояния). Чтобы яснее понять влияние различных факторов на кинетику химической реакции, следует усвоить, что константа скорости зависит ог числа активных молекул, отнесенных к единицам концентрации реагирующих веществ, и от продолжительности нахождения активных молекул в зоне взаимодействия. Обратите особое внимание на кинетику сложных реакций (фотохимические, цепные, гомогенно-каталитические реакции). При количественном описании указанных сложных реакций научитесь применять принцип стационарных концентраций, а при описании цепных реакций изучите теорию Семенова. Обращаем ваше внимание на сложность гетерогенных реакций, состоящих из нескольких стадий. Стадия, протекающая медленнее всех, определяет механизм и скорость гетерогенной реакции, поэтому очень важно знать, на основании каких экспериментальных данных можно определить лимитирующую стадию гетерогенной реакции. Это позволит находить действенные меры для ускорения этих реакций. Учитывая, что в большинстве многотонажных химических производств реакции протекают в присутствии катализатора, следует особое внимание уделять учению о катализе. Надо понять, что если катализатор сохраняет свои свойства неизменными после реакции, то он не может смещать состояния равновесия химической реакции, а только ускоряет момент наступления равновесия.
Вопросы для самопроверки к теме 5: 1. Что такое скорость и константа скорости химической реакции, влияние концентрации реагирующих веществ; молекулярность и порядок (на примере гидролиза 3% водного раствора сахарозы в присутствии 1н HCl)? 2. Как влияет концентрация реагирующих веществ на молекулярность и порядок химической реакции и каков механизм реакции (на примере реакции H2SO4+NaOHизбыток=?). 3. Напишите уравнения константы скорости и периода полупревращения (на примере реакции нулевого порядка СаСО3=СаО+СО2). 4. Перечислите экспериментальные методы определения порядка, константы скорости и периода полураспада (на примере реакции гидролиза 15% раствора сахарозы в присутствии 2н раствора HCl). 5. Как влияет температура на величину скорости и константы скорости реакции? Правило Вант - Гоффа. Энергия активации, ее графическое представление. Уравнение Аррениуса в дифференциальной и интегральной формах. Использование его для определения энергии активации (на примере реакции NaOH+H2SO4= ?). 6. Что такое катализаторы? Причина влияния катализатора на скорость и константу скорости. 12 |
|

 .
.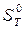 ·
· ,
,  и т. д., f указывает, что это функция образования.
и т. д., f указывает, что это функция образования.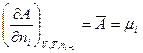
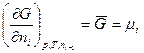
 CuSO4+Cr).
CuSO4+Cr).