|
|
Интегрирование по частям в определенном интегралеДля определенных интегралов имеет место формула интегрирования по частям, аналогичная той, которая была получена для неопределенного интеграла Пусть По формуле Н-Л
Откуда а обобщенная формула интегрирования по частям перейдет в такую:
При этом по прежнему функции Пример 1.
Пример 2 Замена переменного под знаком определенного интеграла Пусть требуется вычислить
Докажем относительно такой замены теорему Th2. Пусть выполнены следующие условия: 1. Уравнения (Обозначим их соотвественно 2. Функция 3. При изменении Тогда имеет место равенство:
Называемое формулой замены переменной под знаком определенного интеграла Доказательство Пусть
Тогда по формуле Ньютона-Лейбница (которая здесь применима, т.к. функция
(т.к. по условию Сопоставляя равенства (2) и (3) мы и получим доказываемую формулу (1)
Замечание. При использовании формулы (1) ф-ю Пределы Лишь бы выполнялись условия 2 и 3 th. Условие th3 окажется, в частности, наверняка выполненным, если ф-я Поэтому на практике замену переменного осуществляют с помощью монотонных функций. Если ф-я
Интегрирование четных и нечетных функций. Th Пусть Тогда Док-во
Пример 1.
Пример 2. Решение. Ф-я
Т.О., подынтегральная ф-я представляет собой произведение четной и нечетной функции, т.е является Замечание. Если ф-я f(x) периодическая с периодом Т то Пример 3. Решение. Подынтегральная ф-я является периодической с периодом Т=
Поэтому от верхнего и нижнего пределов интегрирования можно отнять число π:
Пример 4. Вычислить интеграл.
Решение.
Мы разложили ин-л J в сумму двух интегралов Т.О., чтобы под знаком первого ин-ла стояла нечетная ф-я, а под знаком второго интеграла – четная функция. Тогда
Геометрические приложения опр-го ин-ла. Df1.Фигурой называется
Df2. Фигура наз. квадрируемой (им. Площадь (меру)) если:
p – вписанные в S – многоугольники. Df3. Если фигура S квадрируема, то ее площадью наз-ся
Th1. Фигура “S” квадрируема ó, когда
Th2.
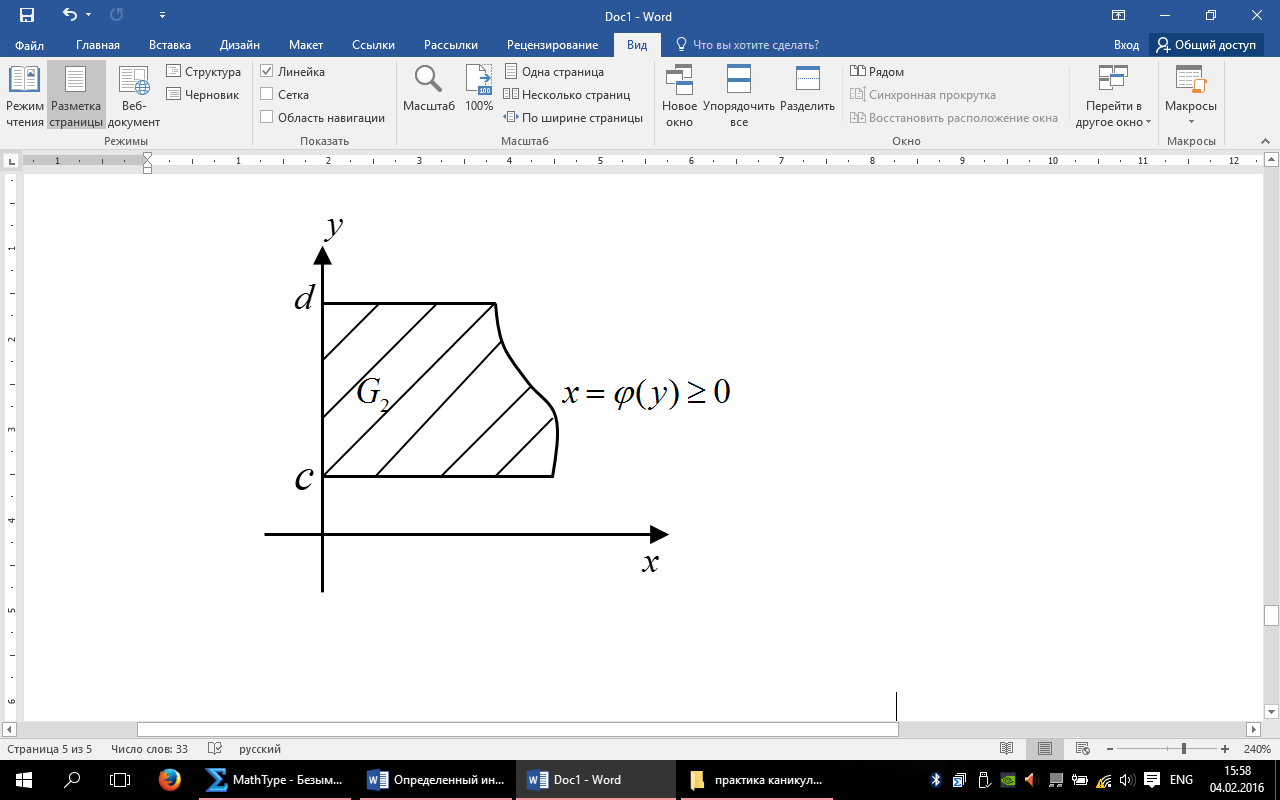
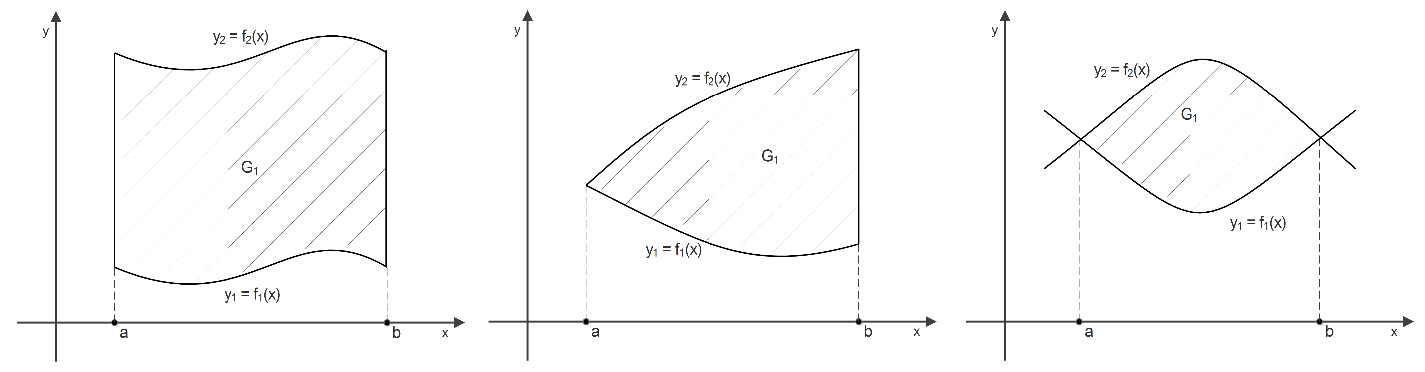
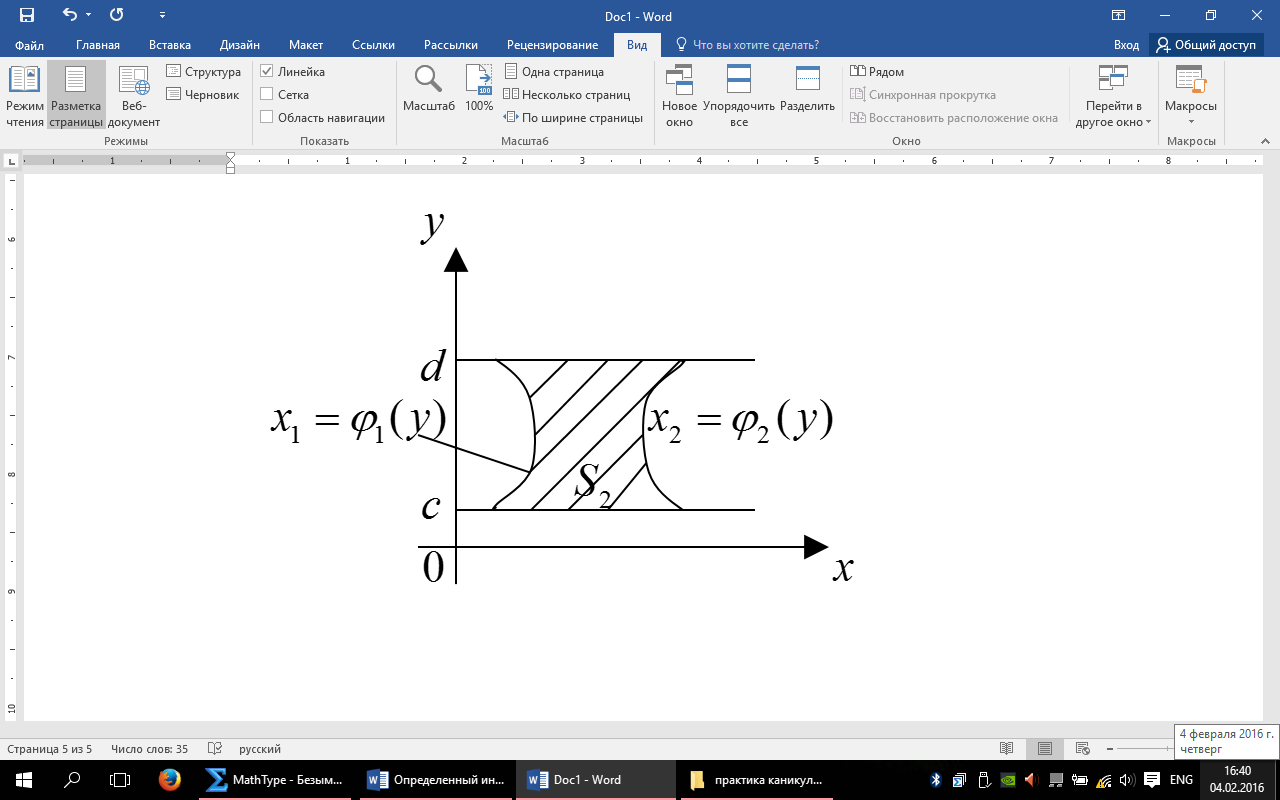
Следствие Если Df4. Криволинейной трапецией. I) 1-го рода (типа) II) 2-го рода (типа) наз-ся I) Где [a,b] – произвольный отрезок на R.
Произвольный отрезок на R, Примеры.

Th3. II) При рассмотрении задачи приводящей к понятию опр-го ин-ла был рассмотрен вопрос о вычислении площади криволинейной трапеции.
Где
Было установлено, что
Частные случаи кр-й огран-ой тр-ии 2-го рода
Огран-ной: Прямыми x=0 , y=c , y=d. Кривой Тогда Пользуясь этими результатами можно вычислить площади разнообразных фигур. Так например
Аналогично и для случая кр.тр. 2го рода.
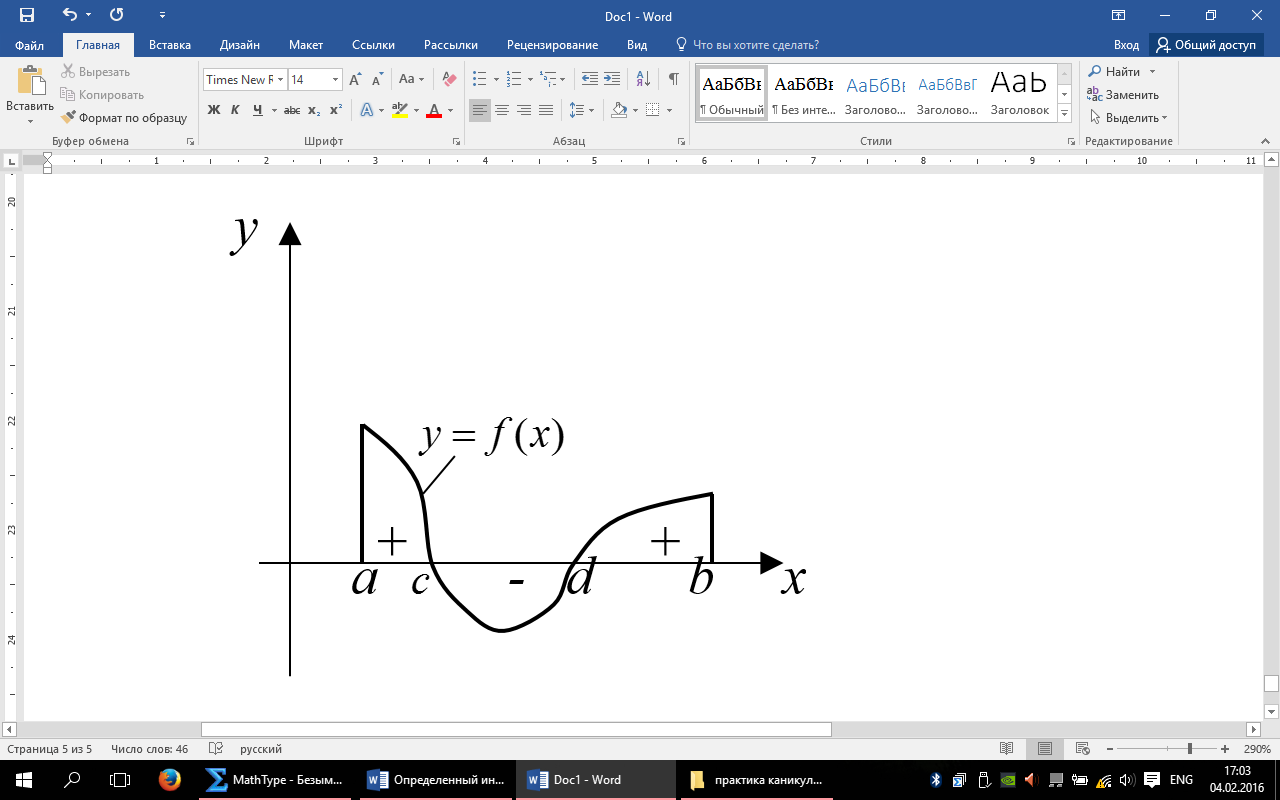
Если

Если Следующим образом.
При x<c f(x)>0; x>c f(x)<0 f(c)=0 x>d f(x)>0 f(d)=0
Df5.
Криволинейным сектором наз-ся
S-площадь криволинейного сектора. Th4.
(б/д) Ур-е кривой задано в параметрической форме
Замечание.
Замечание Если граница фигуры задана параметрическими уравнениями
То площадь фигуры вычисляется по одной из трех формул
Длина дуги кривой Df1 Кривой называется множество Df2 Дугой называется кривая Примеры
Кривая, для которой
Df3 Длиной дуги (АВ) называется Sup|Г|, если Sup Г<∞, то дуга Г вписана в (АВ) спрямляема (имеет длину). Обозначение. Если Г-ломаная, то Утверждение 1) Дуга (АВ) спрямляема 2) Дуга (АВ) спрямляема Гn –ломаная вписанная в дугу (АВ) Df4
Ломанной вписанной в дугу (АВ) называется Обозначается Df5Если
Следствие 1 Если Следствие 2 Если
Или короче Дифференциал дуги Пусть в формуле
Замечание. Пусть дуга кривой AB=1. Задана x=x(t), y=y(t), z=z(t),
Диф-л функции l(t) наз-ся диф-лом дуги кривой AB и обозначается dl. А) если задана дуга кривой Где Если AB лежит в плоскости xoy , т.р.
Б) если плоская кривая AB в полярной системе координат
|
|
 на
на  имеем:
имеем: 

 и кроме того
и кроме того
 или
или  ч.т.д.
ч.т.д.
 и все встречающиеся производные предполагаются непрерывными.
и все встречающиеся производные предполагаются непрерывными.


 от
от  . Иногда, как в неопределенном интеграле бывает удобно произвести замену перестановкой «х» на новую переменную t, которые связаны между собой соотношением:
. Иногда, как в неопределенном интеграле бывает удобно произвести замену перестановкой «х» на новую переменную t, которые связаны между собой соотношением:
 и
и  имеют решения
имеют решения и
и  , так что
, так что  ,
,  )
) (имеет непрерывную производную
(имеет непрерывную производную  на
на  )
) на отрезке
на отрезке  значение функции
значение функции  не выходит из отрезка
не выходит из отрезка  (т.е
(т.е  ) и следовательно сложная функция
) и следовательно сложная функция  определена
определена  (или
(или  ).
). (1)
(1)
 на
на  , тогда по формуле Ньютона-Лейбница имеем
, тогда по формуле Ньютона-Лейбница имеем  (2), рассмотрим на
(2), рассмотрим на 
 функцию
функцию  переменного t определенную соотношением
переменного t определенную соотношением  и
и  . Вычислим ее производному по правилу сложной функции:
. Вычислим ее производному по правилу сложной функции: что функция
что функция  является первообразной для функции
является первообразной для функции  на сегменте
на сегменте  .
. ) имеем:
) имеем: (3)
(3) )
) (1) ч.т.д
(1) ч.т.д следует стараться выбрать так, чтобы новый интеграл был более простым для вычисления, чем первоначальный.
следует стараться выбрать так, чтобы новый интеграл был более простым для вычисления, чем первоначальный. нового интеграла определяются из уравнений:
нового интеграла определяются из уравнений:  и
и  . При этом эти уравнения могут иметь по несколько корней, тогда за
. При этом эти уравнения могут иметь по несколько корней, тогда за  можно принять любой корень уравнения
можно принять любой корень уравнения  любой корень уравнения
любой корень уравнения  будет монотонной на [a,b]
будет монотонной на [a,b] на симметричном относительно начала координат сегменте.
на симметричном относительно начала координат сегменте.



 четна. Докажем, что ф-я
четна. Докажем, что ф-я  нечетна;
нечетна;
 – нечетная ф-я, поэтому J=0
– нечетная ф-я, поэтому J=0

 , т.к
, т.к



 .
.
 замкнутая ограниченная область на плоскости.
замкнутая ограниченная область на плоскости.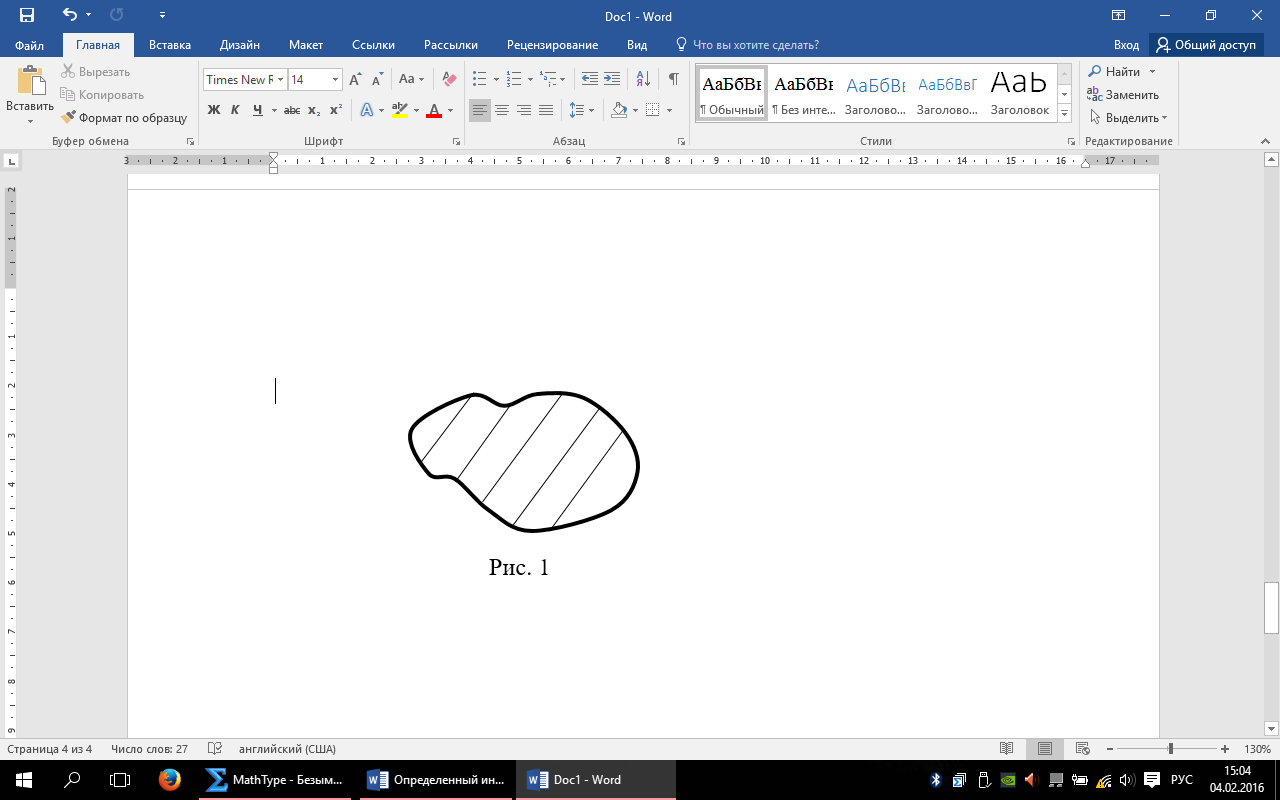

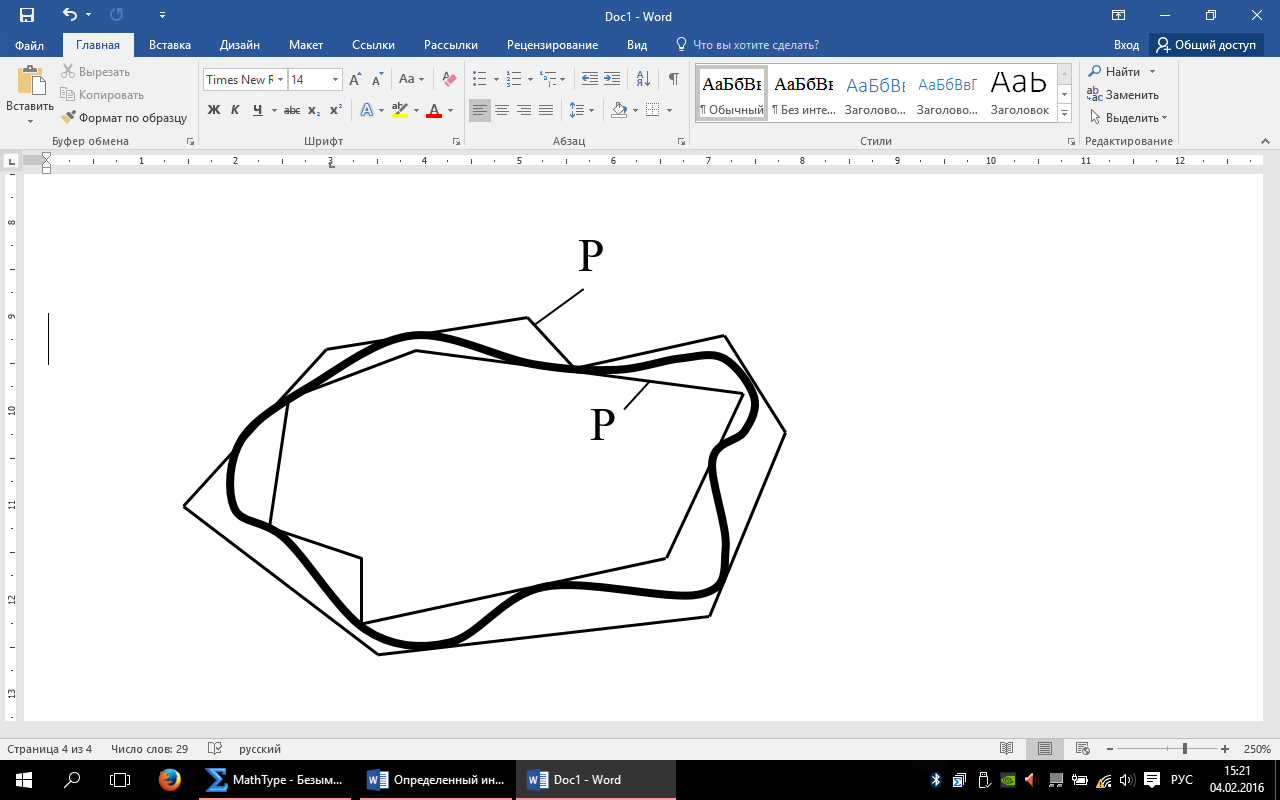

 , где S-данная фигура P-описанные около S многоугольники
, где S-данная фигура P-описанные около S многоугольники

 последовательности
последовательности


 , т.е
, т.е
 - разбиение G, причем две из трех фигур
- разбиение G, причем две из трех фигур  квадрируемы, то квадрируема и третья фигура, причем:
квадрируемы, то квадрируема и третья фигура, причем:


 я замкнутая фигура (область)
я замкнутая фигура (область)  определяемая равенством:
определяемая равенством:
 - произвольные непрерывные на [a,b] удовлетворяющие условиям ф-ции:
- произвольные непрерывные на [a,b] удовлетворяющие условиям ф-ции: 


 удовлетворяющие условиям:
удовлетворяющие условиям: 



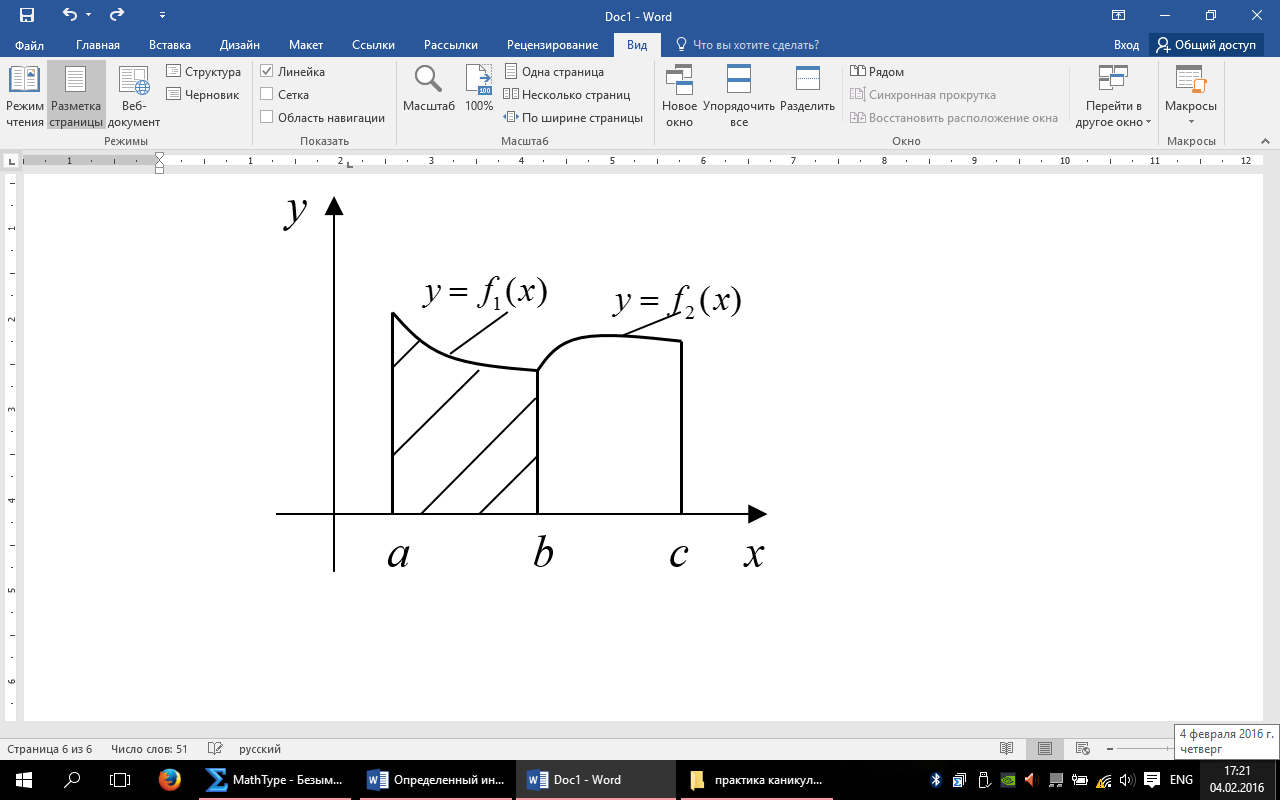
 криволинейная трапеция I)
криволинейная трапеция I)  рода (типа).
рода (типа). рода (типа) – квадрируема.
рода (типа) – квадрируема.









 и не является знакопостоянной на [a,b] , то
и не является знакопостоянной на [a,b] , то  опр-ся
опр-ся

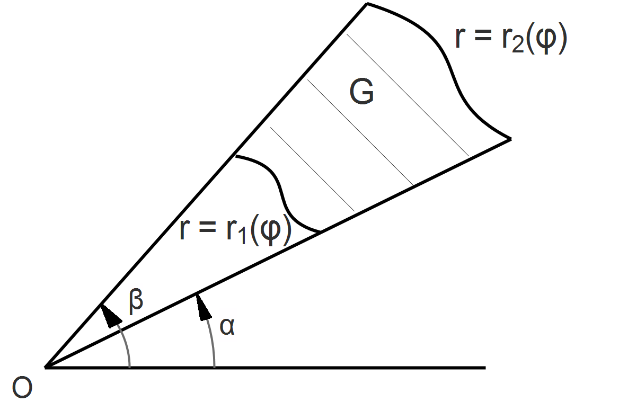
 фигура S, определяемая равенством:
фигура S, определяемая равенством: 
 – произвольный отрезок на [0,2π].
– произвольный отрезок на [0,2π]. - произвольные непрерывные функции на
- произвольные непрерывные функции на  удовлетворяющие условиям
удовлетворяющие условиям 
 криволинейный сектор.
криволинейный сектор.
 Эти функции непрерывны, тогда
Эти функции непрерывны, тогда


 (**)
(**)



 где [α,β] – произвольный отрезок на прямой
где [α,β] – произвольный отрезок на прямой  - произвольная непрерывная вектор- функция – годограф.
- произвольная непрерывная вектор- функция – годограф.
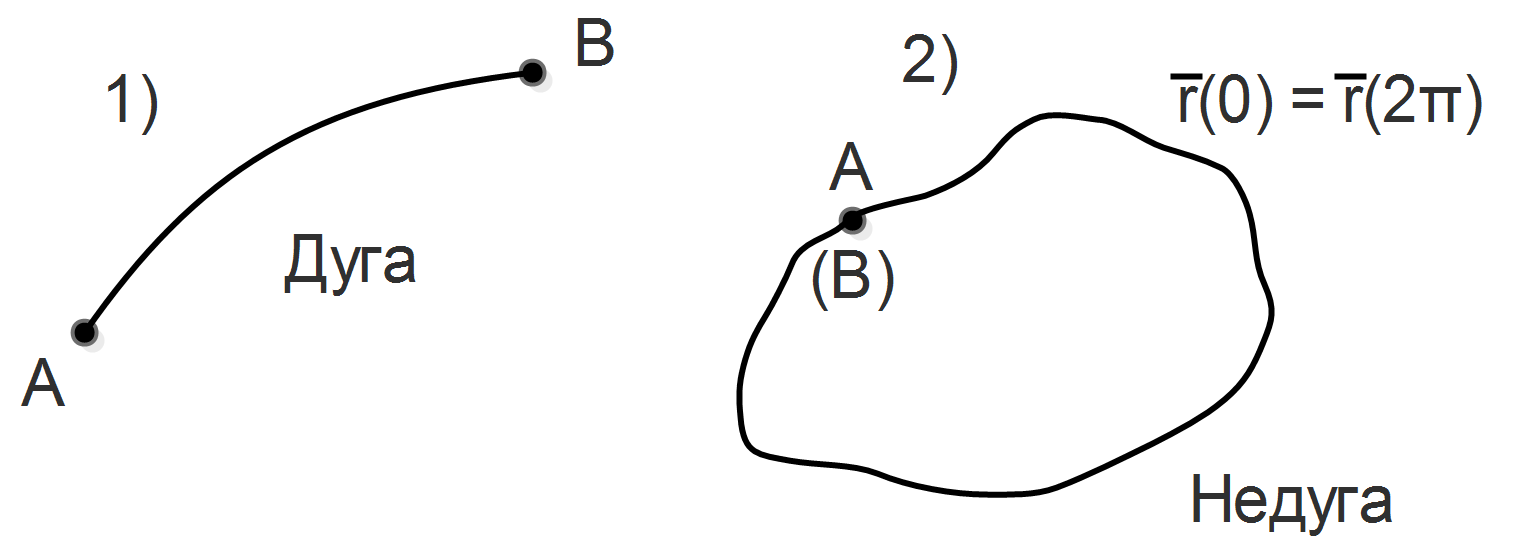
 называется замкнутой (с самопересечением)
называется замкнутой (с самопересечением)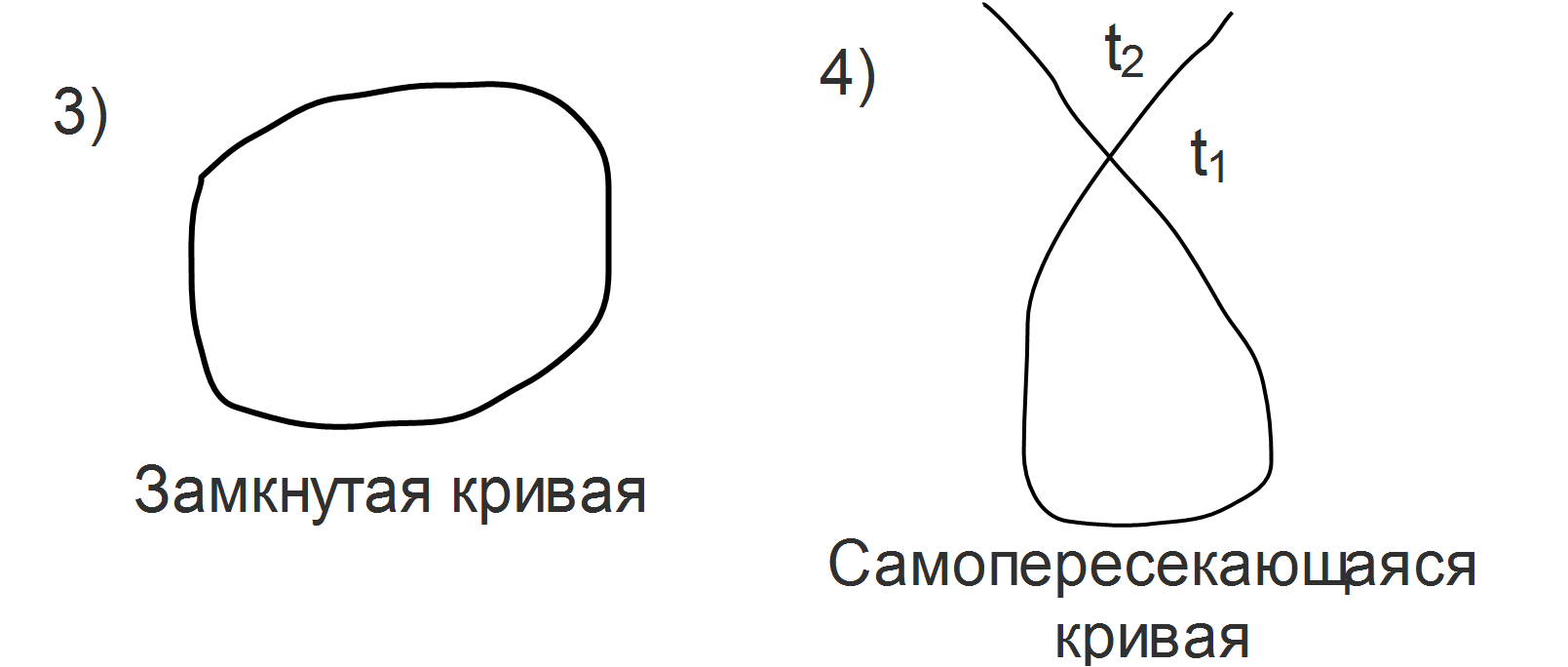
 - max. длина ее звеньев.
- max. длина ее звеньев. , когда
, когда  если
если  , где l-некоторое заданное число l>0, которое равно длине дуги (АВ)
, где l-некоторое заданное число l>0, которое равно длине дуги (АВ) последовательность Гn:
последовательность Гn: 
 -длина дуги
-длина дуги -дуга, где
-дуга, где  -непрерывные диф-мые на [α,β] функции, то
-непрерывные диф-мые на [α,β] функции, то
 где
где  -непрерывная диффиренцируемая на (АВ), то
-непрерывная диффиренцируемая на (АВ), то 

 где r- полярный радиус,
где r- полярный радиус,  -непрерывная диф-ема на [α,β] функция, то
-непрерывная диф-ема на [α,β] функция, то



 нижняя граница «а» остается постоянной, а верхняя граница изменяется. Обозначим верхнюю границу буквой «х», а переменную интегрирования, что бы не смешивать ее с верхней границей – буквой t. Если при этом учесть, что длина дуги «l» есть функция верхней границы, то нашу формулу можно записать в виде:
нижняя граница «а» остается постоянной, а верхняя граница изменяется. Обозначим верхнюю границу буквой «х», а переменную интегрирования, что бы не смешивать ее с верхней границей – буквой t. Если при этом учесть, что длина дуги «l» есть функция верхней границы, то нашу формулу можно записать в виде: , согласно теореме о производной интеграла по верхней границе эта функция диф-ма, и ее производная
, согласно теореме о производной интеграла по верхней границе эта функция диф-ма, и ее производная  дифференциал дуги
дифференциал дуги или, в сокращенной записи,
или, в сокращенной записи,  т.к.
т.к.  ; то
; то  , или
, или  геометр. Смысл дифференциала дуги: дифференциал дуги dl равен длине отрезка касательной от (.) М касания с абсцисой х до (.) М1 с абсцисой х+dx
геометр. Смысл дифференциала дуги: дифференциал дуги dl равен длине отрезка касательной от (.) М касания с абсцисой х до (.) М1 с абсцисой х+dx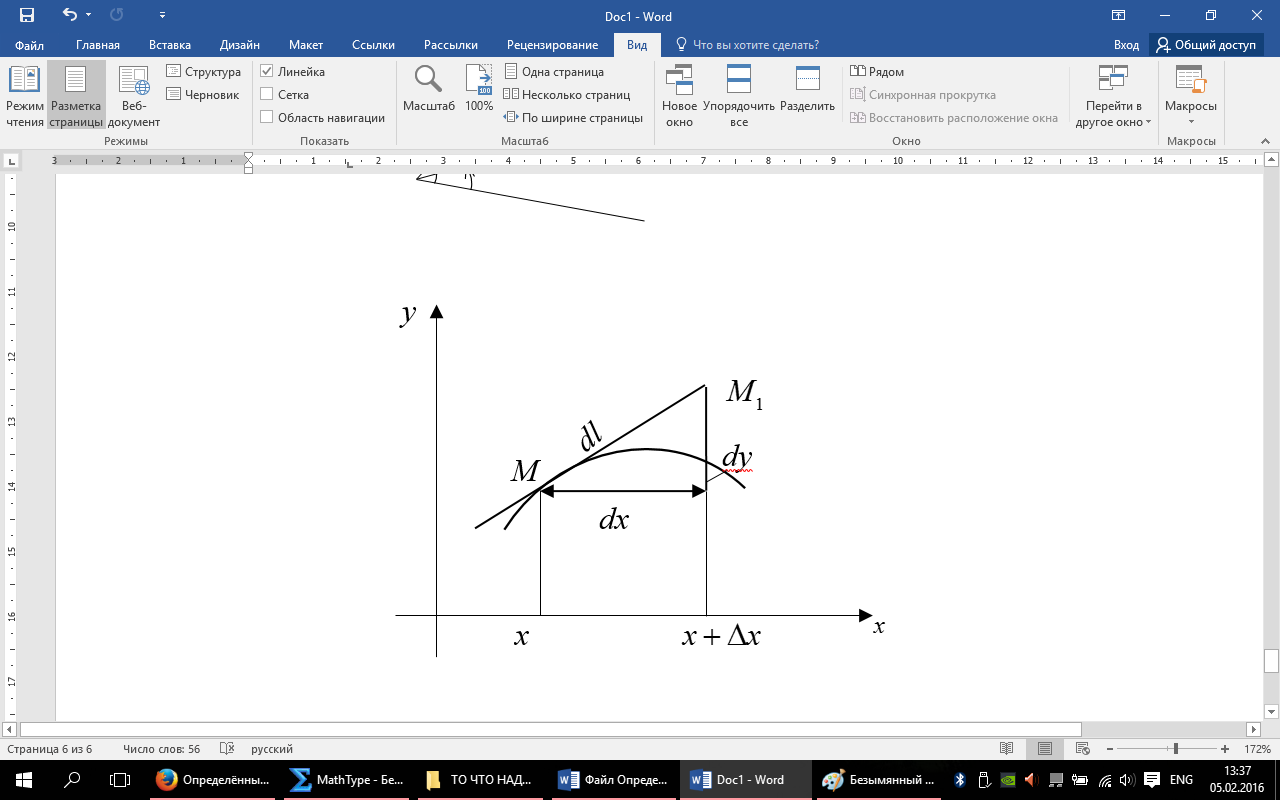
 . Эти функции непрерывно дифференцируемы на
. Эти функции непрерывно дифференцируемы на  . Рассмотрим функцию
. Рассмотрим функцию  длину части кривой AB от начальной (.) A
длину части кривой AB от начальной (.) A до
до 

 то
то 

 , то
, то
