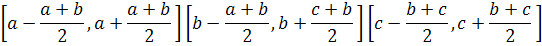|
|
Упрощенный алгоритм нечеткого вывода1. Формирование базы правил Используется правило вида: ЕСЛИ « Где
2. Фаззификация входных переменных Особенности фаззификации совпадают с рассмотренными выше 3. Агрегированния подусловий Как правило, используется логическая операция min-конъюнкция 4. Активизация подзаключений Находятся значения степеней истинности подзаключений с помощью функции min
5. Аккумуляция Фактически отсутствует, т.к. расчеты осуществляются с обычными действительными числами, а не с функциями принадлежности 6. Дефаззификация Используется модифицированный вариант в форме метода центра тяжести для одноточечных множеств
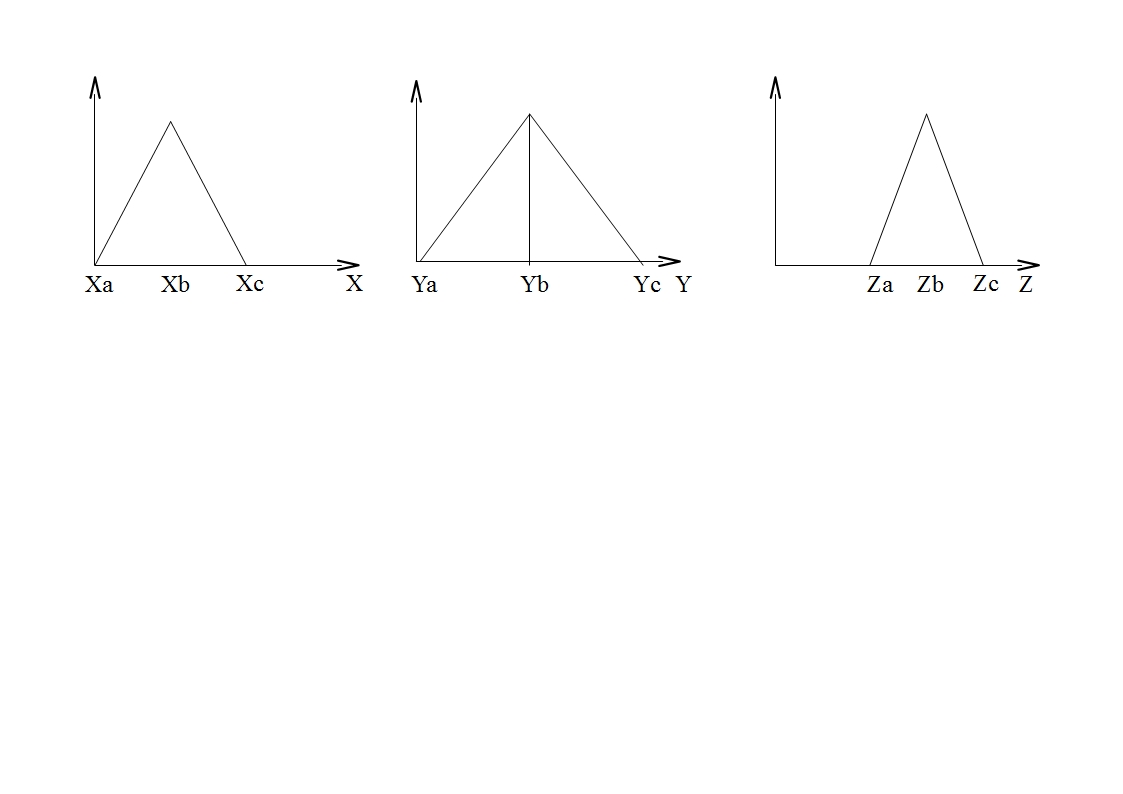
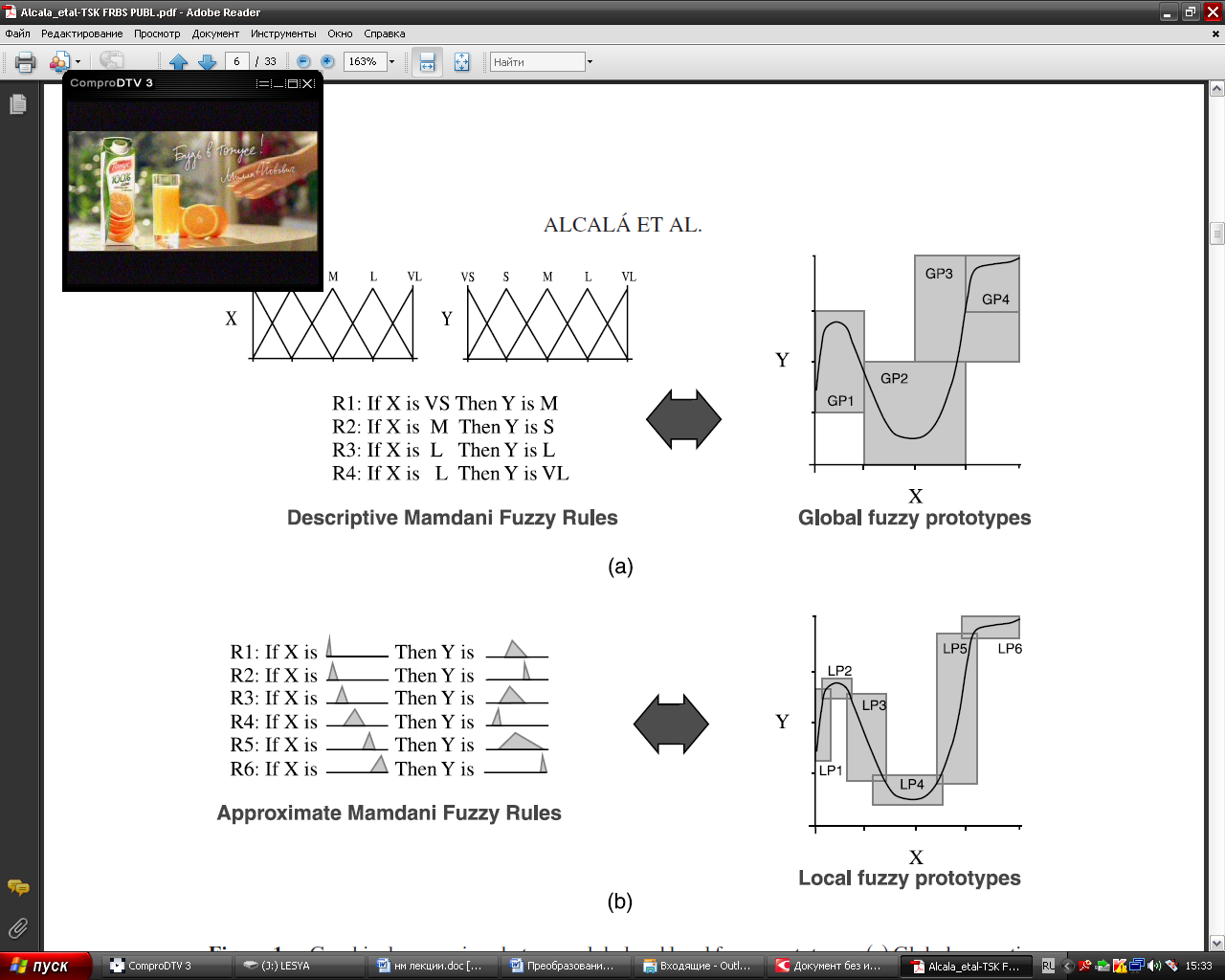
При решении практических задач нечеткого моделирования могут одновременно использоваться несколько алгоритмов нечеткого вывода с целью получения наиболее адекватных результатов. Ниже рассматриваются примеры применения некоторых из этих алгоритмов в задачах нечеткого управления. Разница между представлением результатов полученных с помощью алгоритма Мамдани и Сугена Наглядно разницу можно представить для задачи аппроксимации одномерной функции. Представление Мамдани: Данную функцию можно аппроксимировать с помощью алгоритма Мамдани. Для этого промежуток х разобьем на 6 диапазонов. На каждом из диапазонов поведение функции приблизительно одинаково.
Для каждого из интервалов создаем свое правило. Правила представим в виде треугольной функции:
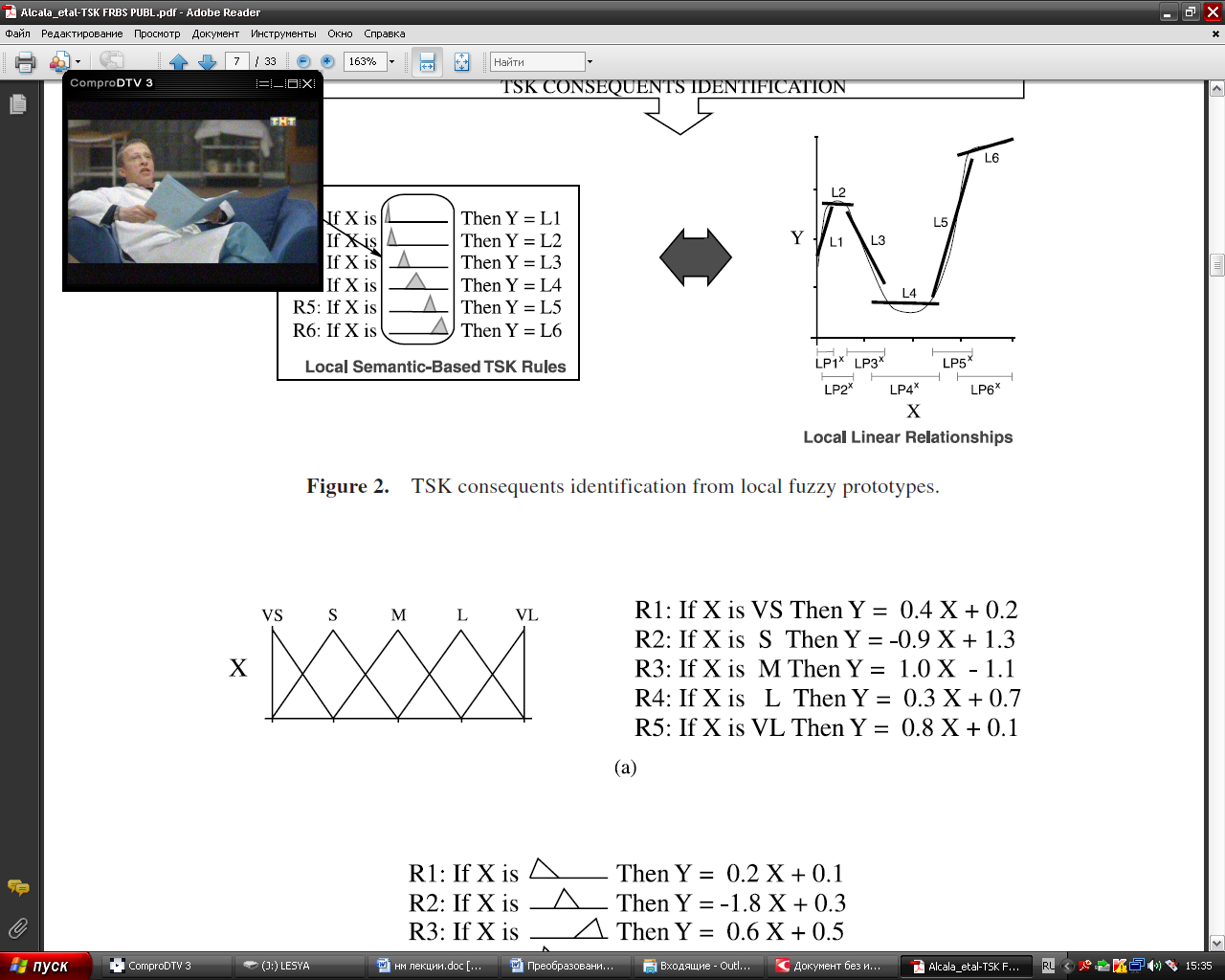
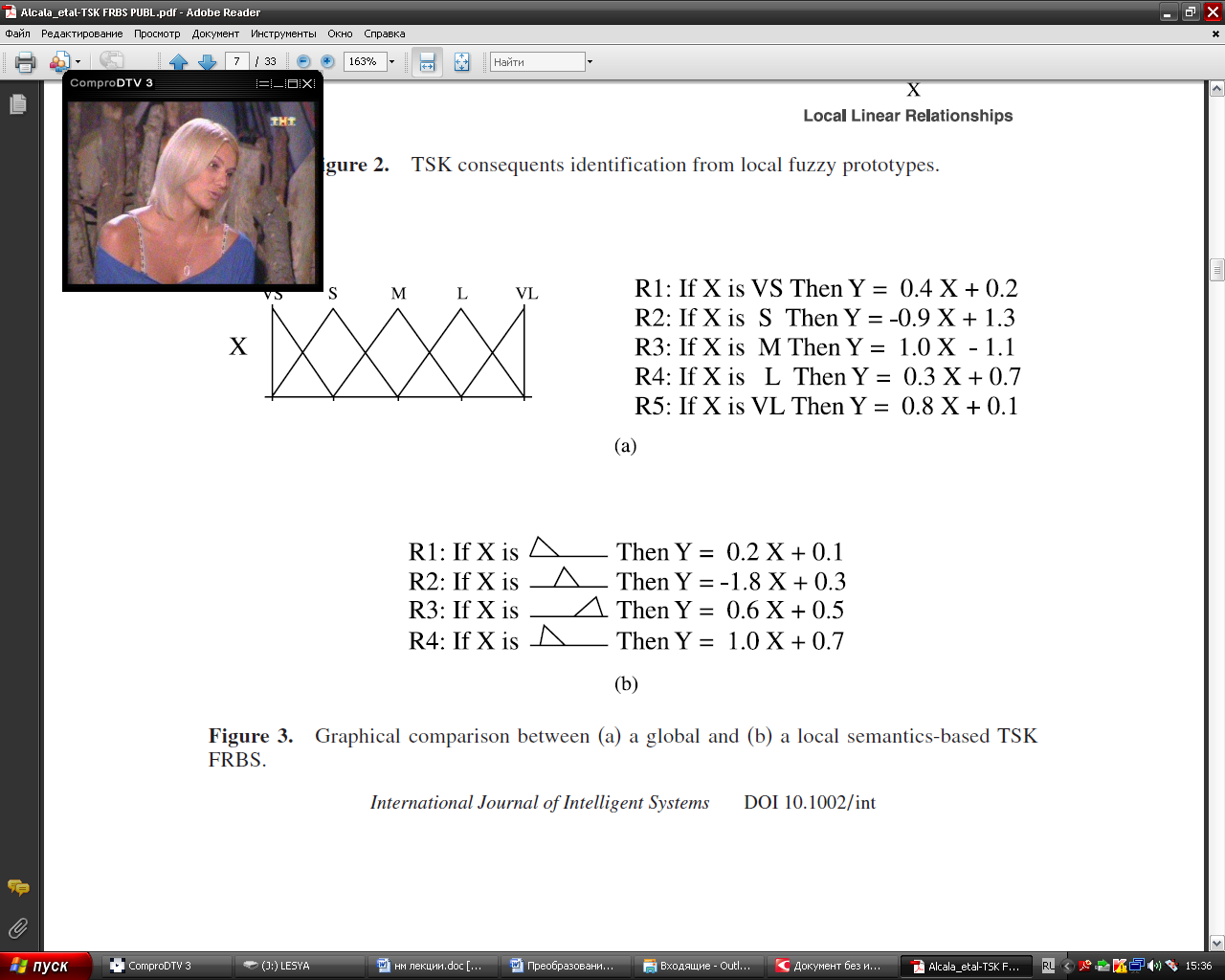
Представление Сугено Эту же функцию можно описать кусочно - линейно с помощью правил по Сугэно. На этих же интервалах представляем участки функции в виде линии.
Преобразование данных для увеличения различимости классов Очень часто бывает, что зависимость представлена точками. При этом плотность заполнения точками различных участков зависимости не будет одинакова. Наиболее часто встречающейся в природе закон распределения – нормальный. Это значит что в центре входного диапазона число точек будет намного выше, чем на краях входного диапазона. И функцию в центре нужно аппроксимировать намного точнее, чем на краях. Это значит, что число правил в центре должно быть больше и точность результата в центре будет больше и имеет большую важность. Это является недостатком, т.к. для любого алгоритма точность на всем промежутке поиска имеет одинаковое значение. Данный недостаток можно исправить если привести распределение данных по входным переменным к равномерному виду. В областях скученности данные необходимо растянуть, в пустых местах - сжать. Преобразование значений исходной входной величины
Физически величине
S(x) является функцией дифференциальной вероятности или функцией распределения величины Для восстановления исходных значений х выполняется обратное преобразование, т.е. находится значение
Для равномерного распределения входных данных вполне логичным будет описание их с помощью лингвистических правил, где термы лингвистических переменных будут создаваться автоматически (например равными треугольниками).
Genetic Fuzzy Systems В настоящее время все более популярными становятся методы автоматического получения набора нечетких правил. Одним из способов автоматического получения нечетких правил является их построение с помощью эволюционных алгоритмов. Также эволюционные алгоритмы могут использоваться для настройки уже построенного набора нечетких правил. В настоящее время направление GFS приобретает все большую популярность.
Построение правил Правила строятся с помощью генетических алгоритмов, используя уже готовые терм-множества. В случае если предметная область хорошо изучена и по каждой из входных переменных созданы экспертами терм-множества ГА могут использоваться для оптимального выбора терма при построении правила.
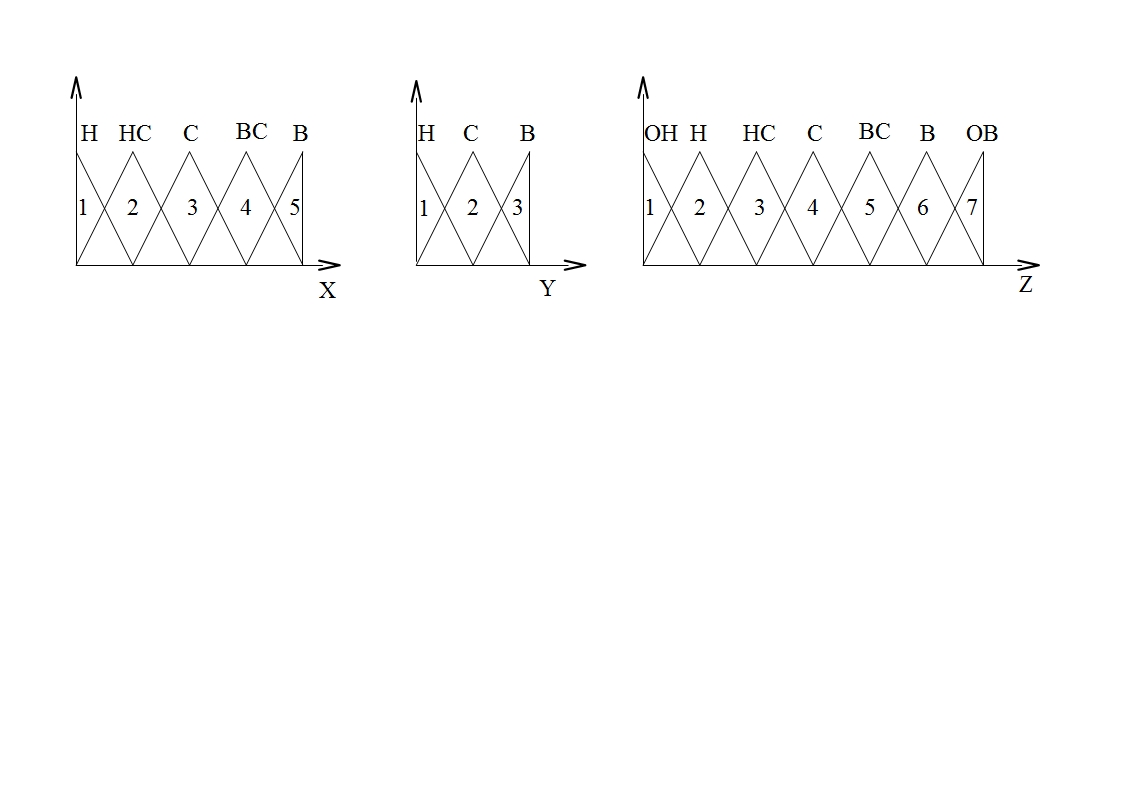
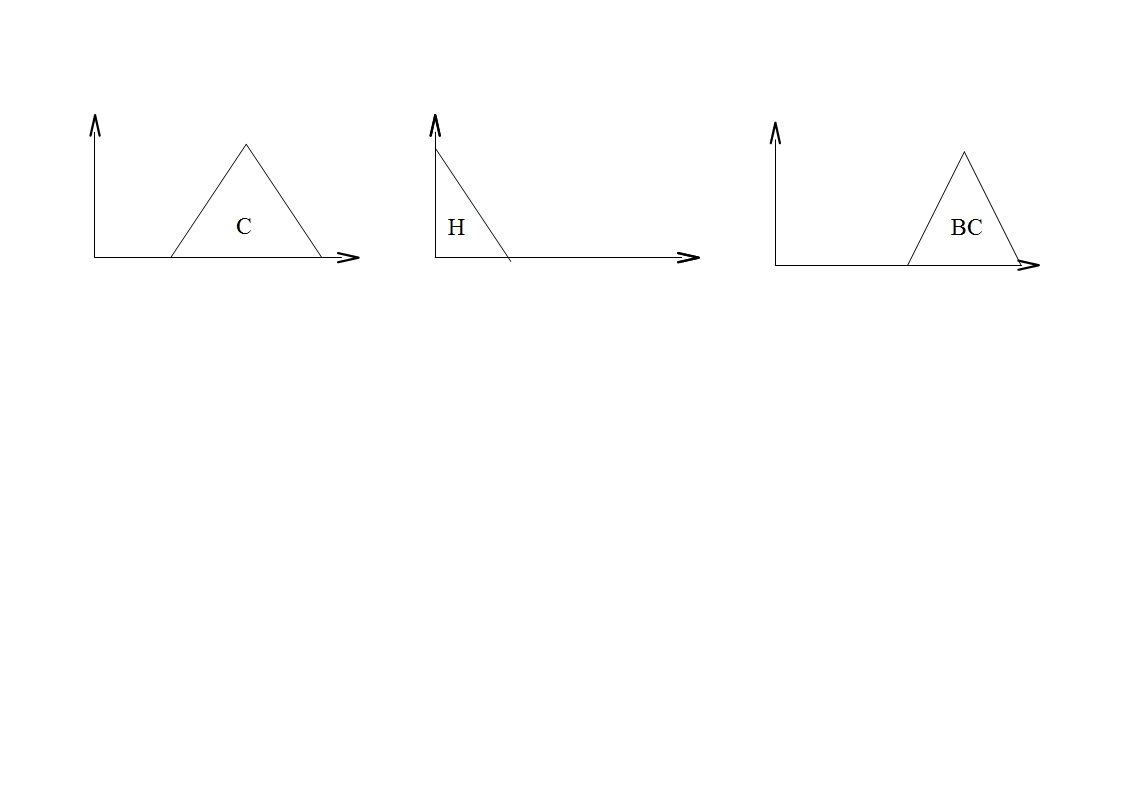
В общем случае число термов в каждом из терм-множеств может отличаться. Для кодировки правила будет логично присвоить каждому из термов свой номер. Правила для данного примера будут состоять из трех чисел. Например, последовательность 3, 1, 5 кодирует следующее правило: ЕСЛИ x1=С и x2=Н то y=ВС
Вид правила также зависит от вида выбранной кодировки правила (смотри выше). Правила могут быть закодированы тремя различными способами: · Все правила хранятся вместе. При этом номер выходного терма хранится в правиле и может быть изменен. · Для каждого из выходных термов создается свой набор правил. Для данного примера будем иметь 7 наборов правил. Каждое из правил кодируется двумя числами – входными ограничениями для x1 и x2. ТО y = ОН: ЕСЛИ x1 = С и x2 = Н 31 ЕСЛИ x1 = В и x2 = Н 51 ЕСЛИ x1 = В и x2 = В 53 · Правила кодируются также как и в первом способе, однако, часть вывод не является независимой и не может быть изменена. Она получается автоматически на основании части условия путем выбора наилучшего терма для заданного условия.
Хромосома генетического алгоритма целочисленная, состоит из n+1 числа, где n – число подусловий или входных переменных и 1 – число выходных переменных. В случае кодировки правил вторым способом хромосома состоит их n чисел. Фитнесс функция генетического алгоритма является мерой точности отклонения полученного с помощью правила результата от того результата, который должен быть получен, т.е. в генетических нечетких системах используется обучение с учителем. Имеем обучающий набор из L точек. Каждая из точек в общем случае содержит n+1 вещественных числа, где n – число входных переменных. После нормировки числа зачастую представляются на интервале от 0 до 1. n=2
Для l точки обучающей выборки и множества из m правил может быть построена прогнозная точка для выходной переменной.
На основании входной точки (x1 , y1) с помощью набора правил может быть получена выходная точка z1, которая в общем случае не будет совпадать с реальным значением z1. Для L входных точек может быть получено L значений В простейшем случае фитесс-функция должна минимизировать среднеквадратичное отклонение величины
Т.е. при получении фитнесс-функции работают одновременно все правила, причем работают они L раз, где L – число точек обучающей выборки. Создание популяции правил может происходить случайно. Операторы кроссинговера используются такие, которые применимы для целочисленного кодирования хромосом (лаб.работа №1 по ГА). Операторы мутации или случайное создание подусловия, или инкремент (декремент) номера терма. Фитнесс-функция – точность, получаемая с помощью только одного данного правила. Пример
Допустим, имеются правила:
С помощью операции репродукции отобрано 2 пары:
Получены потомки для которых найдена своя функция:
Затем потомки могут быть добавлены в исходную популяцию, а затем она должна быть сокращена или потомки могут полностью заменить исходную популяцию. Недостаток: Крайне низкое пространство поиска генетического алгоритма. Для данного примера возможно 5*3*7=105 правил. Точность описания предметной области крайне низкая и пространства поиска у генетического алгоритма практически нет. Целесообразность применения генетического алгоритма в данном случае отсутствует. Кодирование с помощью термов хотя и является логичным и интуитивно понятным, однако, не может выдать достаточно точный результат. Точность описания набора данных будет заранее низкая. Однако, такой подход имеет право на жизнь, хотя и с некоторыми дополнениями для улучшения точности. Подход, при котором в правилах кодируются номера термов, называется дискриптивным. Существует также другой подход, при котором в правиле кодируется непосредственно форма функции принадлежности. Такой подход называется аппроксимативным. Для треугольных правил для кодирования одного подусловия необходимо три вещественных числа:
В аппроксимативном подходе форма функции принадлежности кодируется непосредственно в правиле. Для кодирования одного правила с двумя подусловиями и одним заключением необходимо девять вещественных чисел, тогда генетический алгоритм будет работать с вещественными числами и использовать операторы рекомбинации, применимые для вещественного кодирования хромосомы(min max кроссинговер и неравномерная мутация) – см. ЛР№2 по ГА. Такой подход позволяет получать намного лучшую точность, однако, интерпретируемость результатов крайне не высока, т.к. результаты нельзя описать словами. Существует также комбинированный метод, который включает в себя преимущества обоих методов: · На первом этапе Выбираются термы из терм множеств xa xb xc ya yb yc za zb zc
· На втором этапе Коэффициенты a, b, c функций принадлежности могут меняться, подстраиваясь под конкретный набор данных Задается разрешенный диапазон изменения координат треугольника. Для координат a, b и c:
Правило будет состоять из двух частей: 1 часть. Определяет выбор терма из терм-множества. Для каждого подусловия задается одно число – номер терма. 2 часть. Уточняет вид функции принадлежности каждого из подусловий. Каждое из подусловий кодируется тремя вещественными числами. Для трех подусловий правило в этом случае будет состоять из 12 чисел: nx ny nz | xa xb xc ya yb yc za zb zc Первые три числа целые, последние девять чисел - вещественные. Генетический алгоритм работает отдельно с каждой из двух частей правила. Генетический алгоритм с целочисленным кодированием хромосомы осуществляет грубый подбор терма для подусловий. После того, как терм выбран, начинает работать генетический алгоритм с вещественным кодированием хромосомы для того, чтобы максимально подстроить форму функции принадлежности. В случае замены какого либо номера терма из первой части правила соответствующие координаты a, b и c второй части правила берутся из терм множества неизменными. n1x n1y n1z | x1a x1b x1c y1a y1b y1c z1a z1b z1c n2x n2y n2z | x2a x2b x21c y2a y2b y2c z2a z2b z2c Генетический алгоритм смотрит, одинакова ли первая часть двух особей. В случае если она одинакова, выполняется вещественный генетический алгоритм для подстройки функций принадлежности подусловий. Иначе, работает целочисленный генетический алгоритм, который комбинирует различные термы из первой части правила.
Процесс генерации правил Генерация правил осуществляется тремя различными способами: 1 способ Треть начальной популяции создается так: часть с1 правила заполняется таким образом, чтобы выбрать терм, лучше всего покрывающий множество обучающих точек. Часть с2 заполняется из терм множеств. 2 способ Заполняется вторая треть выборки. Часть с1 заполняется выбором наилучшего терма, покрывающего точки обучающей выборки. Часть с2 заполняется случайно в пределах разрешенного интервала для каждого терма. 3 способ. Последняя треть множества особей заполняется следующим образом: часть с1 заполняется случайно, часть с2 - в пределах разрешенного интервала.
|
|
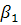 есть
есть 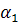 » И «
» И « 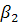 есть
есть  » ТО «
» ТО « 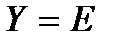 »
»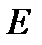 - это некоторое действительное число
- это некоторое действительное число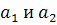 - степени активации 1 и 2 подусловий
- степени активации 1 и 2 подусловий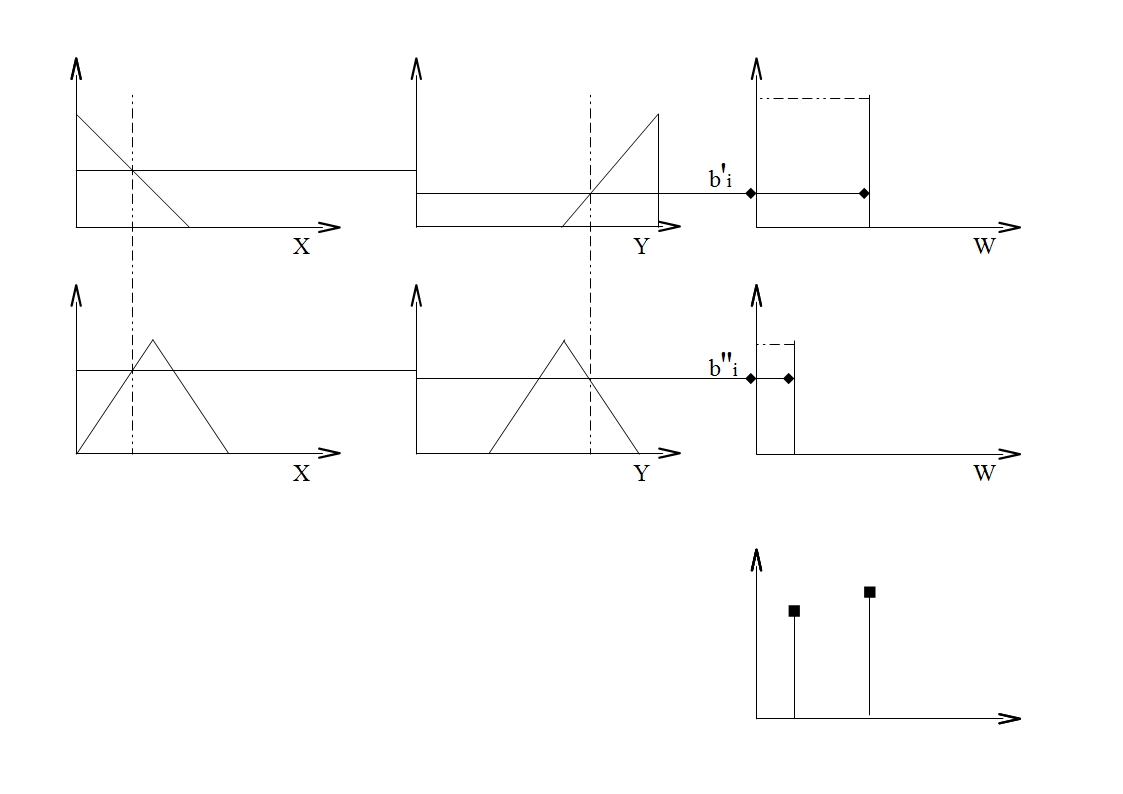

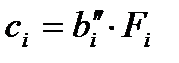
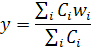
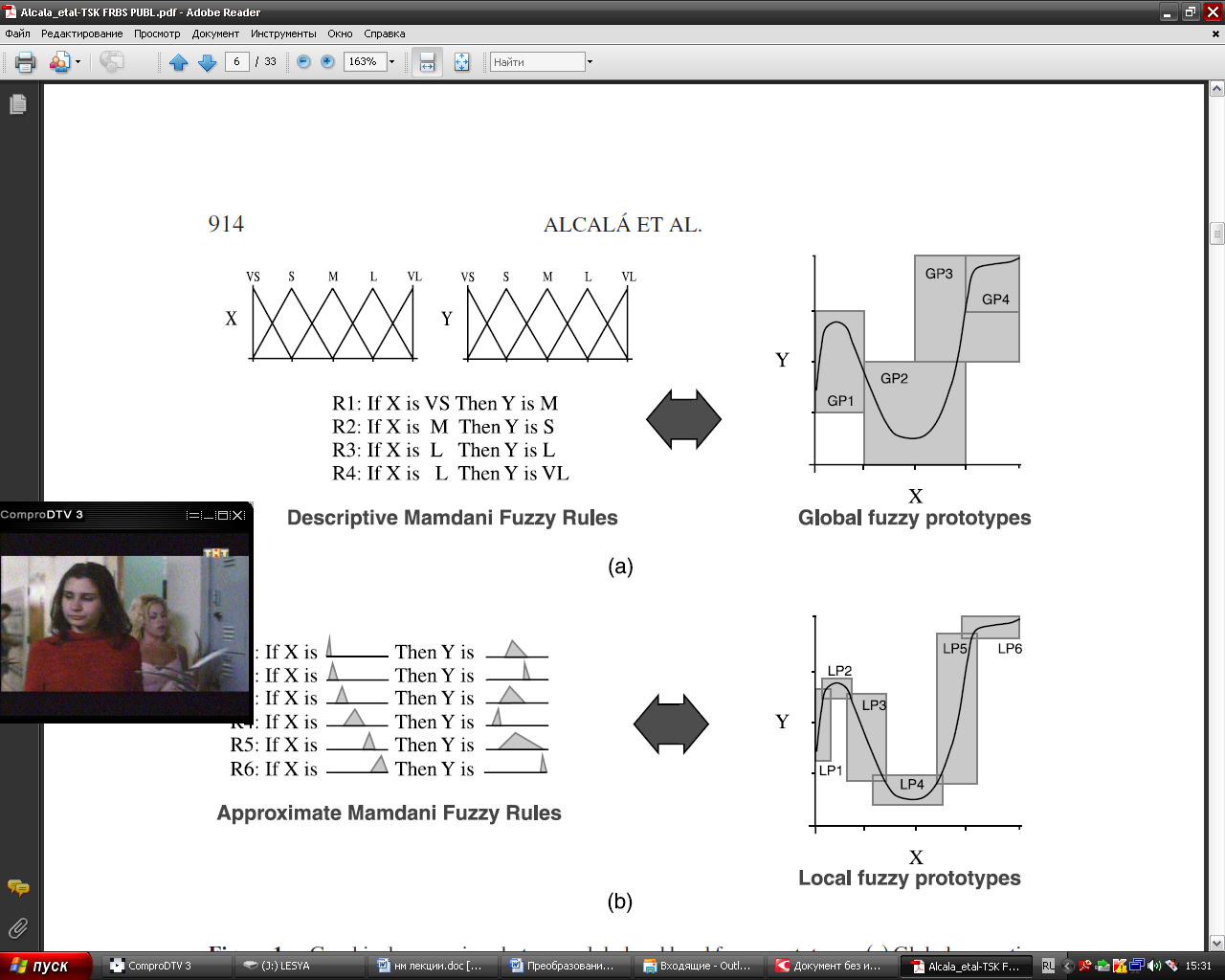
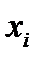 выполняется в соответствии с плотностью их распределения Р(x). Значение преобразованной величины
выполняется в соответствии с плотностью их распределения Р(x). Значение преобразованной величины 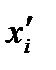 вычисляется:
вычисляется: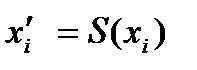 где
где 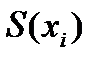 - функция распределения значений
- функция распределения значений 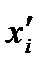 соответствует площадь
соответствует площадь 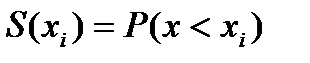
 .
.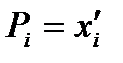
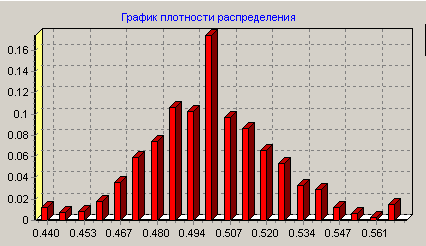 Плотность распределения исходной ОВ.
Плотность распределения исходной ОВ.
 Функция распределения исходной ОВ.
Функция распределения исходной ОВ.
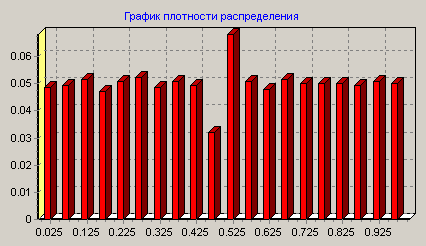 Плотность распределения преобразованной ОВ.
Плотность распределения преобразованной ОВ.
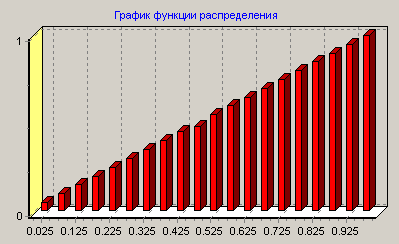 Функция распределения преобразованной ОВ.
Функция распределения преобразованной ОВ.








 [0…1]
y
[0…1]
y 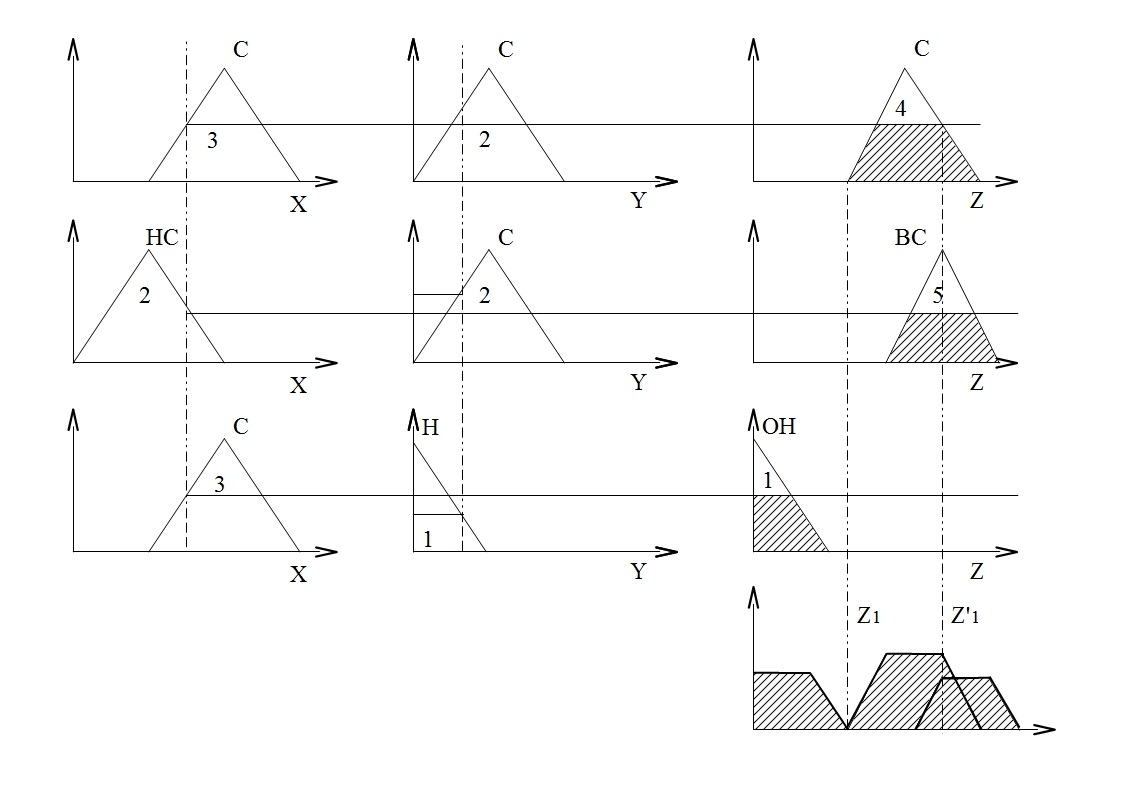
 , которые отличаются от значений zi – реальных значений выходной переменной.
, которые отличаются от значений zi – реальных значений выходной переменной.