|
|
Методы измерений и описание аппаратурыПУТЕЙ СООБЩЕНИЯ» Кафедра «Физика» ФИЗИКА Механические колебания МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНЫМ РАБОТАМ по дисциплине «Физика» Работы 4, 5, 5а, 105 МОСКВА - 2012
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛБНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»
Кафедра «Физика»
ФИЗИКА
Механические колебания
Под редакцией доцента В.А. Селезнева
Рекомендовано редакционно-издательским советом университета в качестве методических указаний для студентов ИУИТ, ИТТСУ, ИЭФ, ИПСС
МОСКВА -2012
УДК 534 Л 97
Лагидзе Р.М., Лямзова И.А. Физика. Механические колебания. Методические указания к лабораторным работам по физике. Работы 4, 5, 5а, 105. / Под редакцией доцента В.А. Селезнева. – М.: МИИТ, 2012. – 32 с.
Методические указания к лабораторным работам по физике № 4, 5, 5а, 105 соответствуют программе и учебным планам по курсу общей физики (раздел «Колебания и волны») и предназначены для студентов всех специальностей.
ã МИИТ, 2012
Работа 4
ИЗУЧЕНИЕ СВОБОДНЫХ КОЛЕБАНИЙ ПРУЖИННОГО МАЯТНИКА
Цель работы: Определение коэффициента жесткости пружины по удлинению пружины и методом колебаний пружинного маятника.
Введение
Рассмотрим простейшую колебательную систему: груз массой m, подвешенный на пружине. Упругая сила растяжения пружины в положении равновесия равна силе тяжести груза и, будучи направлена вверх, уравновешивает ее. При выведении груза из положения равновесия пружина действует на него с дополнительной силой F, пропорциональной смещению x (при малых смещениях) и направленной в сторону противоположную смещению:
F = – kx,
где k – коэффициент жесткости пружины; он равен численному значению силы, которую нужно приложить к пружине, чтобы растянуть (или сжать) ее на единицу длины. Единица измерения коэффициента жесткости – [k] = Н×м-1. Груз, выведенный из положения равновесия, начнет совершать относительно него гармонические колебания:
x = A sin (ωt + φ0), (1)
где А – амплитуда колебания; (ωt + j0) – фаза колебания; ω – круговая частота; j0 – начальная фаза колебания. Энергия, сообщенная системе пружина-груз при начальном толчке, будет периодически преобразовываться: потенциальная энергия упруго деформированной пружины ЕП = Согласно закону сохранения энергии для консервативной системы механическая энергия E = ЕП + ЕК= В момент прохождения грузом положения равновесия (x = 0) из формулы (2) следует, что полная энергия системы E = ЕК max = Согласно уравнению (1), скорость гармонически колеблющегося груза u = а максимальная скорость umax = ωA. (3)
В крайних положениях груза (u = 0, x = ±A) энергия системы переходит полностью в потенциальную Еп:
E = ЕП max = По закону сохранения энергии
Подставляя выражение (3) в соотношение (4), получим mω2 = k, ω = Учитывая, что ω = T = 2p Таким образом, период не зависит от амплитуды колебаний и определяется только величинами m и k. Амплитуда и начальная фаза колебаний j0 определяются начальными условиями, при которых возникло движение. Приборы и принадлежности.Штатив с пружиной и зеркальной шкалой, держатель для грузов, набор грузов, секундомер.
Порядок выполнения работы
I. Определение коэффициента жесткости пружины k по удлинению пружины
1. Подвесить к концу пружины держатель (рис. 1).
Рис. 1
2. Пользуясь зеркальной шкалой, заметить начальное положение держателя l0 (отсчет делают таким образом, чтобы нижняя грань держателя совпала с его зеркальным изображением) и записать данные отсчета в таблицу 1.
3. Постепенно нагружать держатель грузами (их масса в граммах маркирована на них), записывая положение нижней грани держателя l1 для каждого значения растягивающей силы, соответствующей общей массе m грузов (масса держателя в m не входит).
4. Нагрузив держатель всеми грузами, начинают их по одному снимать, записывая в таблицу в обратном порядке снизу-вверх соответствующее положение нижней грани держателя l2 для каждого значения m.
5. Вычислить среднее арифметическое величин l1 и l2 для каждой массы lСР =
6. Вычислить удлинение пружины для каждого значения массы грузов вычитая l0 из соответствующего lСР: Δl = lСР – l0.
Таблица 1
7. Построить проходящий через начало координат график зависимости удлинения пружины Δl от массы m (рис. 2).
8. Рассчитать погрешность определения коэффициента жесткости по формуле Dk = k Для расчета погрешности следует использовать те значения m и Δl, по которым рассчитывался коэффициент жесткости, а в качестве Δ(Δl), Δm и Δg взять приборную погрешность измерения удлинения и учесть точность, с которой задаются массы грузов и ускорение свободного падения. Результат расчета k и погрешности его определения Δk занести в таблицу 1, выполнив предварительно соответствующее округление [4].
II. Определение коэффициента жёсткости k пружины по зависимости периода собственных колебаний пружинного маятника от массы груза
1. Поместить на держатель груз. Значение массы груза с держателем M и результаты последующих измерений занести в таблицу 2. Измерить секундомером время 10 полных колебаний маятника. Опыт повторить не менее 4 раз. Найти среднее значение времени tср 10 полных колебаний и среднее значение периода колебаний ТСР =
2. Подобные измерения провести для различных значений грузов. Таблица 2
III. Определение коэффициента жесткости пружины методом колебаний
1. По результатам проведенных измерений построить проходящий через начало координат график зависимости квадрата периода колебаний Т2 от массы M, предварительно рассчитав Тср2 для каждого значения M. Выбрав одну из полученных в эксперименте точек, лежащую на усредненной прямой, рассчитать коэффициент жесткости пружины по формуле kСР = 4p2 2. Оценить погрешность полученного результата. При условии, что ошибка в определении числа колебаний отсутствовала, эту погрешность можно рассчитать по формуле Dk = k В качестве Ошибка определения времени колебаний определяется как
Dt =
Систематическую погрешность в определении времени ΔtСИСТ, связанную с конечной скоростью реакции человека, можно принять равной 0,1 с: t = tСЛ + tСИСТ. Случайную ошибку ΔtСЛ следует рассчитать по методу Стьюдента:
ΔtСЛ = an,P
Для числа колебаний N = 4 и доверительной вероятности P = 0,95 коэффициент Стьюдента an,P = 3,2. Окончательный результат записать в таблицу 2. Сравнить полученное значение коэффициента жесткости пружины с результатом, полученным ранее по методу измерения удлинения пружины (часть I).
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Какие деформации называются упругими? Сформулируйте закон Гука. 2. Какие колебания называются свободными? 3. Получите формулу для периода колебаний пружинного маятника. 4. Чем можно объяснить различие в значениях коэффициента жесткости, полученных разными методами?
Список литературы
1. Детлаф А.А., Яворский Б.М. Курс физики. –М.: Высш. шк. – 2000. 2. Савельев И.В. Курс физики. – Т. 2. – М.: Наука – 1998 и далее. 3. Трофимова Т.И. Курс физики. – М., 2000 и далее. 4. Селезнёв В.А., Тимофеев Ю. П. Вводное занятие в лабораториях кафедры физики. – М.: МИИТ. – 2011. – 38 с.
Работа 5 ИЗУЧЕНИЕ СВОБОДНЫХ КОЛЕБАНИЙ ФИЗИЧЕСКОГО МАЯТНИКА
Цель работы. Определение момента инерции физического маятника по периоду его малых колебаний и приведенной длине.
Введение
Физическим маятником называется любое твёрдое тело, совершающее колебания под действием силы тяжести вокруг горизонтальной оси, не проходящей через центр инерции тела. Всегда можно подобрать математический маятник, синхронный данному физическому, то есть такой математический маятник, период колебаний которого равен периоду колебаний физического маятника. Длина такого математического маятника называется приведённой длиной физического маятника. Выведем формулу периода колебаний физического маятника.
На рис. 1 точка O – след горизонтальной оси вращения, точка B – центр тяжести (следует отметить, что в однородном поле сил тяжести центр инерции и центр тяжести совпадают).
Относительно оси вращения сила тяжести создает вращающий момент
М = mgd sinj, (1)
где m – масса физического маятника, d – кратчайшее расстояние от оси вращения до центра тяжести маятника, j – угловое отклонение маятника, отсчитываемое от положения равновесия. Угловое отклонение φ можно рассматривать как вектор, лежащий на оси вращения, направление которого определяется направлением поворота тела из положения равновесия в заданное положение по правилу правого винта. Учитывая, что векторы Тогда формула (1) примет вид
М = – mgd sinj. (1.а)
При малых углах φ можно принять sinj » j, если j выражен в радианах, и записать формулу (1.а) следующим образом:
М = – mgd j. (2)
Используем основной закон динамики вращательного движения тела относительно неподвижной оси, записав его в проекциях на ось вращения: М = Jb, (3)
где J – момент инерции тела относительно оси вращения; а β – угловое ускорение, причем β = Подставляя в формулу (3) выражение M из формулы (2), получим уравнение движения маятника
Решение полученного дифференциального уравнения второго порядка с постоянными коэффициентами можно записать в виде
j(t)=j0cos(w0t + a0), (5) где, w0 = Величины j0 и (w0t + a0) называют соответственно амплитудой и фазой колебания, a0 – начальной фазой. Уравнение (5) является уравнением гармонического колебательного движения, а величина ω0 называется циклической собственной частотой колебания. По истечении времени T =
TФ = 2p
Известно, что период колебаний математического маятника записывается в виде TМ = 2p
Сравнивая эту формулу с формулой (6), делаем вывод, что математический маятник будет иметь тот же период колебаний, что и данный физический, если длина математического маятника
l =
Это и есть формула приведённой длины lП физического маятника.
Методы измерений и описание аппаратуры
Прибор, используемый в данной работе, представляет собой настенный кронштейн, на котором смонтированы подушки для опорных призм физического маятника. На том же кронштейне подвешен математический маятник, длину которого можно изменять, наматывая нить на соответствующий барабанчик. Физический маятник представляет собой цилиндрический стержень (рис. 2), на котором жестко закреплены две призмы 1 и 2. На стержне находятся также два тяжелых груза 3 и 4 в форме чечевиц, один из которых (3) закреплен, а другой может перемещаться по шкале и закрепляться в нужном положении. Расстояние между опорными призмами равно 0,730 м. Масса маятника m = 10,55 кг (Δm = 0,01 кг). Один из методов определения момента инерции маятника относительно горизонтальной оси, проходящей через опорную призму, сводиться к определению периода колебаний Т маятника относительно этой оси, массы m и расстояния d от центра тяжести до оси (см. формулу (6) для ТФ). В этом случае момент инерции маятника вычисляется по формуле J =
Положение центра тяжести можно определить с помощью призмы балансировки. Кроме этого метода, на практике часто используют метод определения момента инерции по приведённой длине физического маятника. Приведённую длину находят из опыта, подбирая такой математический маятник, который колеблется синхронно с данным физическим. Определив длину математического маятника lП находят момент инерции по формуле J = mlПd. (9)
Приборы и принадлежности: физический маятник, математический маятник, секундомер, линейка, штангенциркуль, призма балансировки.
Порядок выполнения работы
Первый метод 1. Подвесив маятник на призме 1 (см. рис. 2), отклонить его на небольшой угол (менее 10°) и измерить секундомером время десяти (n = 10) колебаний. Измерения произвести пять раз. Затем произвести аналогичные измерения, подвешивая маятник на призме 2. Данные занести в таблицу 1. Вычислить tСР, а затем найти период по формуле T = tСР/n. Результат занести в таблицу 1.
Таблица 1
Для определения расстояний d от центра тяжести до осей вращения снять маятник с опоры и положить на специальную подставку (призму балансировки). На подставке, которая имеет острую грань, маятник необходимо уравновесить. Расстояние от точки, находящейся над гранью призмы балансировки, до опорных призм измерить масштабной линейкой с точностью до Δd = 0,001 м. Результаты занести в таблицу 1, затем рассчитать моменты инерции по формуле (8). Результаты занести в таблицу 3.
Второй метод Изменяя длину математического маятника, добиться того, чтобы он колебался синхронно с физическим. Полного совпадения периодов обоих маятников добиться нелегко. Поэтому следует, постепенно меняя длину нити математического маятника, добиться того, чтобы маятники колебались синхронно в течение 10 – 15 колебаний. Измерить расстояние от шарика до точки подвеса. Длина маятника равна этому расстоянию плюс радиус шарика (диаметр шарика измерить штангенциркулем). Её можно считать приведённой длиной lП физического маятника. Результаты занести в таблицу 2. Момент инерции вычислить по формуле (9) и результат занести в таблицу 3.
Подобные измерения и расчёты повторить, подвешивая маятник и на второй призме. Таблица 2
Таблица 3
|
|

 будет переходить в кинетическую энергию движущегося груза ЕК =
будет переходить в кинетическую энергию движущегося груза ЕК = и обратно.
и обратно. +
+  = const. (2)
= const. (2) .
. = Aωcos(ωt + j0),
= Aωcos(ωt + j0), .
. .
. , получим выражение для периода колебаний Т:
, получим выражение для периода колебаний Т: . (5)
. (5)
 .
.
 , взяв значения m и Δl для любой точки усредненной прямой.
, взяв значения m и Δl для любой точки усредненной прямой. .
. , где n = 10, при расчетах оставляя на одну значащую цифру больше, чем в результатах наблюдений.
, где n = 10, при расчетах оставляя на одну значащую цифру больше, чем в результатах наблюдений. .
.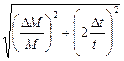 .
. принимается точность, с которой задаются масса держателя и грузов.
принимается точность, с которой задаются масса держателя и грузов. .
. .
.
 , стремящийся возвратить маятник в положение равновесия. Численное значение модуля этого момента определяется соотношением
, стремящийся возвратить маятник в положение равновесия. Численное значение модуля этого момента определяется соотношением антипараллельны, следует величинам проекций вращающего момента и углового перемещения на ось вращения приписать противоположные знаки.
антипараллельны, следует величинам проекций вращающего момента и углового перемещения на ось вращения приписать противоположные знаки. =
=  .
. j = 0. (4)
j = 0. (4) , а j0 и a0– постоянные, определяемые начальными условиями.
, а j0 и a0– постоянные, определяемые начальными условиями. фаза получает приращение 2p, а тело возвращается в исходное положение с сохранением направления движения. Величина T называется периодом колебания. Таким образом, период колебания физического маятника определяется формулой
фаза получает приращение 2p, а тело возвращается в исходное положение с сохранением направления движения. Величина T называется периодом колебания. Таким образом, период колебания физического маятника определяется формулой , (6)
, (6) .
. = lП. (7)
= lП. (7) mgd. (8)
mgd. (8)