|
|
Решение нелинейных уравненийЗадача решения уравнения вида F(X)=0встречается в различных областях науки и техники (здесь F(x) – некоторая непрерывная функция). Нелинейные уравнения можно разделить на два класса – алгебраические и трансцендентные. Алгебраическими уравнениями называют уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные). В частности, многочлен является алгебраической функцией. Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и др.) называются трансцендентными. Многие нелинейные уравнения не имеют аналитического решения, поэтому они решаются численными методами с заданной пользователем (TOL=3 – по умолчанию до третьего знака) точностью. Для простейших уравнений используется встроенная функция root (выражение, имя_переменной, [a,b]), где a, b – диапазон, в котором ведется поиск корней.
Рис.1.7. Решение уравнения с помощью оператора root (обратите внимание, как еще можно задать начальное значение переменной). Первый тип функции root требует дополнительного задания начального значения (guess value) переменной х. Для этого нужно просто предварительно присвоить х некоторое число. Поиск корня будет производиться вблизи этого числа. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня. Для поиска корней полинома (многочлена) степени n, коэффициенты которого находятся в векторе V, имеющим длину, равную n+1, имеется функция polyroots(V).
Рис. 1.8. Определение корней полинома В приведенном выше примере использован итерационный метод. Как известно, кубическое уравнение обязательно имеет хотя бы один действительный корень x1. Он найден в начале решения функцией root. Два других корня могут быть и комплексными. Функция root может отыскать и эти корни. Для поиска второго корня x2 первый исключается делением F(x) на (x-x1). Соответственно для поиска третьего корня x3 F(x) делится еще и на (x-x2). Эту процедуру можно распространить и на поиск корней полиномов более высоких степеней. Однако следует помнить, что найти корни можно и более изящным способом – используя операцию символьных вычислений.
Рис. 1.9. Использование оператора solve Для получения численного значения приведенного выше примера достаточно поставить знак равенства после скобки решения и нажать <Enter>. Но не рекомендуется пользоваться функциейpolyroots, если полином выше пятой-шестой степени, т.к. трудно получить малую погрешность вычислений корней. Коэффициенты рассматриваемого в примере полинома f (х) = (х-3 ) (х-1)3=х4-6х3 + 12х2-10х+3 записаны в виде вектора в первой строке листинга. Первым в векторе должен идти свободный член полинома, вторым – коэффициент при х1 и т. д. Соответственно, последним n+1 элементом вектора должен быть коэффициент при старшей степени Xn. Иногда исходный полином имеется не в развернутом виде, а, например, как произведение нескольких полиномов. В этом случае определить все его коэффициенты можно, выделив его и выбрав в меню Symbolic (Символика) пункт Expand (Разложить). В результате символьный процессор Mathcad сам преобразует полином в нужную форму, пользователю надо будет только корректно ввести ее в аргументы функции polyroots.
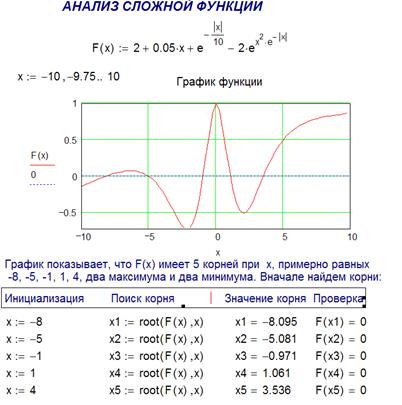
Рис. 1.10. Использование векторной записи коэффициентов полинома Ввод коэффициентов полинома (первая строка листинга) осуществляется применением шаблона из панели Матрицы (Matrix). Во второй строке листинга показано действие функции polyroots. Обратите внимание, что численный метод вместо двух из трех действительных единичных корней (иными словами, кратного корня 1) выдает два мнимых числа. Однако малая мнимая часть этих корней находится в пределах погрешности, определяемой константой TOL, и не должна вводить пользователей в заблуждение. Просто нужно помнить, что корни полинома могут быть комплексными, и ошибка вычислений может сказываться как на действительной, так и на комплексной части искомого корня. Еще один пример. Построение графика помогает грубо определить координаты корней.
Рис. 1.11. Использование графика для поиска корней Для решения систем уравнений используется блок, открываемый служебной функцией Given и имеющий следующую структуру: Given (дано) Уравнения Ограничительные условия Выражения с функциями Find (найти), Minerr (минимальная ошибка), Maximize, Minimize.
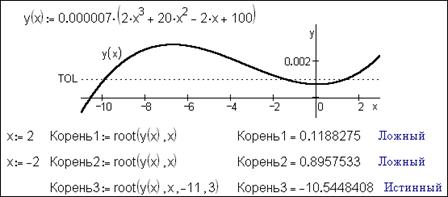
На качество работы функции root влияет значение системной переменной TOL. На рисунках 1.8 и 1.11 эта переменная по умолчанию была равна 10-3: мы не свели уравнение к тождеству 0 = 0, а сделали так, чтобы правая и левая части по модулю отличались не более, чем на 10-3. Функция Find решает систему так, чтобы левые и правые части входящих в нее уравнений отличались на величину, не превышающую значения TOL. Значение TOL, по умолчанию, 0.001, его можно изменить. Но и это часто не помогает. Так вот, только при строго определенных начальных условиях пакет MathCAD находит правильное решение. В качестве примера приведем решение нелинейного уравнения (рис. 1.13).
Как видно из листинга программы MathCAD дает ложный корень в близи нуля (п.6). На следующем рисунке это показывается более наглядно. В среде MathCAD 2000 и выше изменилась работа встроенной функции root. Теперь эта функция может иметь либо два, либо четыре аргумента. Два аргумента означает прежнее содержание этой функции – поиск корня уравнения с опорой на начальное приближение, а четыре – поиск корня в заданном интервале. На рисунке 1.14 «двухаргументная» функция root дает сбои, а «четырехаргументная» – нет.
Рис. 1.14. Применение «четырехаргументного» параметра С другой стороны смягчить эту проблему можно с другого конца – ввести в выражения балластные (нормирующие) коэффициенты, уравнивающие их по отношению друг к другу и позволяющие им решаться с одной точностью. В теме 3 приведены примеры решения задач, которые необходимо выполнить в задании №1. Работа выполняется каждым студентом самостоятельно. Задачи по теме 3, которые необходимо выполнить, находятся в таблицах 1.15 – 1.16. Номер варианта определяется по последней цифре номера зачётной книжки студента. Тема 4. Численное решение дифференциальных уравнений в Mathcad В теме 4 приведены материалы для самостоятельного изучения по решению дифференциальных уравнений. §1. Используемые инструменты MathCAD Запишем систему дифференциальных уравнений в векторной форме: Y’ = F(x, Y), Y(x0)=Y0 где Y – искомое решение, Y0 – вектор начальных условий, F (x, Y) – вектор правых частей. В MathCAD решить задачу Коши для такой системы можно с помощью следующих встроенных функций: · rkfixed (y, x1, x2, npoints, D) – решение задачи на отрезке методом Рунге-Кутта с постоянным шагом; · Rkadapt (y, x1, x2, npoints, D) – решение задачи на отрезке методом Рунге-Кутта с автоматическим выбором шага; · Rkadapt (y, x1, x2, acc, npoints, D, kmax, save) – решение задачи в заданной точке методом Рунге-Кутта с автоматическим выбором шага; · bulstoer (y, x1, x2, npoints, D) – решение задачи на отрезке методом Булирша-Штера; · bulstoer (y, x1, x2, acc, npoints, D, kmax, save) – решение задачи в заданной точке методом Булирша-Штера; · stiffr (y, x1, x2, acc, D, J) – решение задачи для жестких систем на отрезке с использованием алгоритма Розенброка; · stiffr (y, x1, x2, acc, D, J) – решение задачи для жестких систем в заданной точке с использованием алгоритма Розенброка; · stiffb (y, x1, x2, acc, D, J) – решение задачи для жестких систем на отрезке с использованием алгоритма Булирша-Штера; · stiffb (y, x1, x2, acc, D, J) – решение задачи для жестких систем в заданной точке с использованием алгоритма Булирша-Штера. Смысл параметров для всех функций одинаков и определяется математической постановкой задачи: · y – вектор начальных условий Y0, yi=(Y)i; · x1, x2 – начальная и конечная точки отрезка интегрирования системы; для функций, вычисляющих решение в заданной точке, x1 – начальная точка, x2 – заданная точка; · npoints – число узлов на отрезке [x1, x2]; при решении задачи на отрезке результат содержит npoints+1 строку; · D – имя вектора-функции D(x, y), содержащей правые части F(x, Y), Di(x,y)=fi(x, y1,…, yn); · J – имя матрицы-функции J(x, y) размерности n*(n+1), в которой содержится матрица Якоби (Якобиан) правых частей; · acc – параметр, контролирующий погрешность решения при автоматическом выборе шага интегрирования (если погрешность решения больше acc, то шаг сетки уменьшается; шаг уменьшается до тех пор, пока его значение на станет меньше save); · kmax – максимальное число узлов сетки, в которых может быть вычислено решение задачи на отрезке (максимальное число строк в результате); · save – наименьшее допустимое значение шага для функции с автоматическим выбором шага. Результат работы функции – матрица, содержащая n+1 столбец; ее первый столбец содержит координаты узлов сетки, второй столбец – вычисленные приближенные значения решения y1(x) в узлах сетки, (k+1)-й – значение решения yk(x). В библиотеке встроенных функций MathCAD есть функция odesolve, предназначенная для решения линейных дифференциальных уравнений. Функцияodesolve решает задачу Коши с начальными условиями: y(x0)=y0, y’(x0)=y0,1,…, y(n-1)(x0)=y0,n-1 или простейшую краевую задачу, в которой заданы n граничных условий, определяющих значения искомой функции y(x) и ее производных в концах отрезка [a, b], т.е. заданы n граничных условий вида y(k)(a)=ya,k, y(m)(b)=yb,m, 0 ≤ k ≤ n-1 , 0 ≤ m ≤ n-1 Перед обращением к функции odesolve (x, b,step) или odesolve (x, b) необходимо записать ключевое слово Given , затем ввести уравнение и начальные либо граничные условия. Здесь x – имя переменной интегрирования (аргумента искомой функции), b – правый конец отрезка интегрирования, step – шаг, который используется при интегрировании уравнения методом Рунге-Кутта (этот аргумент можно опустить). При вводе уравнения и условий задачи используется знак символьного равенства (<Ctrl> + <=>), а для записи производных можно использовать как оператор дифференцирования, так и знак производной. Например, вторую можно ввести в виде:
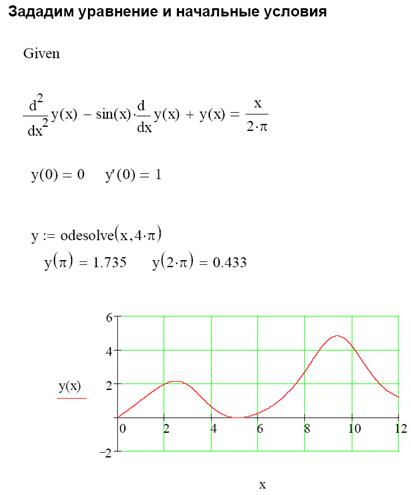
Функция odesolve решает поставленную задачу методом Рунге-Кутта с фиксированным шагом. Для решения задачи методом Рунге-Кутта с автоматическим выбором шага нужно щелкнуть правой кнопкой мыши и пометить в контекстном меню пункт Adaptive. Задание 1. Решение задачи Коши для линейного дифференциального уравнения. Найдем с помощью функции odesolve на отрезке [0, 4π] решение задачи Коши
Фрагмент документа MathCAD, содержащего вычисления и график решения, приведен ниже. Введение первой производной в строке начальных условий возможно с использованием комбинации клавиш <Ctrl>+<F7>.Листинг решения приведен на рисунке 1.15.
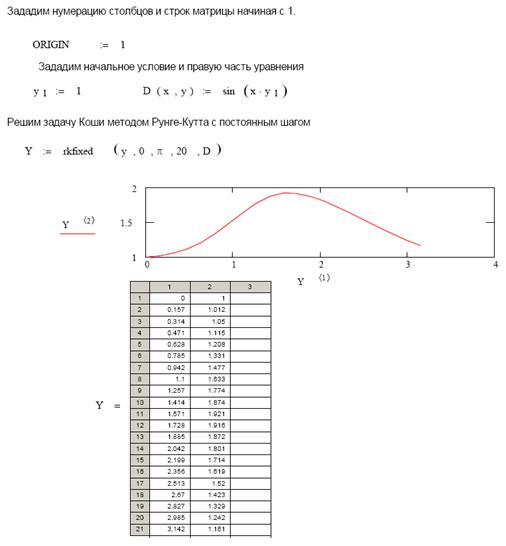
Рис. 1.15. Листинг решения задания 1 Задание 2. Решение задачи Коши для дифференциального уравнения первого порядка. Найдем на отрезке [0, π] приближенное значение решения уравнения y’=sinxy, удовлетворяющее начальным условиям y(0)=1, и построим график найденного решения. Решим задачу численно, используя алгоритм Рунге-Кутта с фиксированным шагом на сетке из 20 равностоящих узлов. Листинг решения приведен на рисунке 1.16.
Рис. 1.16. Применение метода Рунге-Кутта В строке для Y – первый столбец матрицы Y-Y<1> содержит значения 20 узлов сетки на отрезке [0, π], второй столбец (Y<2>) соответствующие значения решения. Для ввода <1> следует использовать панель Матрицы или <Ctrl>+<6>. Возможно, таблица решения будет неполной. Для этого следует щелкнуть мышкой по таблице и расширить ее. Задание 3. Решение задачи Коши для дифференциальных уравнений высших порядков. Найдем на отрезке [0, 3] приближенное решение уравнения y”=e-xy, удовлетворяющее начальным условиям y(0)=1, y’(0)=1, и построим график найденного решения. Введем решение задачи для уравнения второго порядка к задаче для эквивалентной нормальной системы второго порядка. Обозначим y1(x)=y(x) и y2(x)=y’(x). Поскольку y” (x)=(y’(x))’=y’2(x), то получим:
Решим задачу численно, используя алгоритм Рунге-Кутта с фиксированным шагом на сетке из 20 равноотстоящих узлов. На рисунке 1.17 приведен фрагмент документа MathCAD. Первый столбец Y<1> матрицы Y содержит значения 30 узлов сетки на отрезке [0, 3], второй столбец – соответствующие значения y(x) , третий столбец Y<3> ‑ значения y2 (значения y’(x)).
Задание 4. Решение задачи Коши для нормальной системы дифференциальных уравнений. Найдем на отрезке [0, 3] приближенное решение задачи Коши:
и построим графики для найденного решения. Решим задаче, используя алгоритм Рунге-Кутта с фиксированным шагом на сетке из 30 равноотстоящих узлов. При решении этой задачи все действия в Mathcad выполняются аналогично приведенному выше Заданию 3. Для получения нескольких кривых на одном графике следует имена функций перечислить через запятую. Первая строка листинга ORIGIN:=1 указывает на то, что все нижние индексы начинаются с 1, а не с 0, как по умолчанию.
Рис. 1.18. Решение системы дифференциальных уравнений
Задание №1 Применение программы MATHCAD для решения численных и аналитических задач Цель работы: изучение возможностей программы MathCAD для решения численных и аналитических задач. Работа выполняется каждым студентом самостоятельно. Номер варианта определяется по последней цифре номера зачётной книжки студента. Тема 1. Символьные вычисления с использованием встроенных операторов пакета MathCAD 1.1. Упростить выражение из таблицы 1.1 с применением встроенного оператора Simplify Таблица 1.1
1.2. Разложить по степеням выражение, взятое из таблицы 1.2, с применением встроенного оператора Expand. Таблица 1.2
1.3. Разложить на множители выражение, взятое из таблицы 1.3, с применением встроенного оператора Factor. Таблица 1.3
1.4. Разложить выражение по подвыражению, используя процедуру Collection Subexpression. Выражение взять из таблицы 1.4. Таблица 1.4
1.5. Определить коэффициенты полинома, используя встроенную процедуру Coeffs. Выражение взять из таблицы 1.5. Таблица 1.5
1.6. Продифференцировать выражение, взятое из таблицы 1.6. Таблица 1.6
1.7. Проинтегрировать выражение, взятое из таблицы 1.7. Таблица 1.7
1.8. Произвести подстановку тождества f1(x) в выражение y(x), применив оператор Substitute. Выражение y(x) и тождество f1(x) взять из таблицы 1.8. Таблица 1.8
1.9. Разложить функцию f(x) в ряд Тейлора в окрестности точки x = 0 и взять первых девять членов ряда. Определить погрешность представления данной функции с помощью ряда для точки x = x0. Функцию f(x) и величину x0 взять из таблицы 1.9. Таблица 1.9
1.10. Разложить относительно переменной x на элементарные дроби выражение, взятое из таблицы 1.10, с применением процедуры Parfrac. Таблица 1.10
1.11. Найти пределы функции, согласно варианту, из таблицы 1.11. Таблица 1.11
Тема 2. Матричная алгебра 2.1. Транспонировать матрицу, взятую из таблицы 1.12. Таблица 1.12
2.2. Найти обратную матрицу от известной матрицы, взятой из таблицы 1.13. Таблица 1.13
2.3. Вычислить аналитически определитель матрицы
Получить численный ответ с применением оператора Substitute, при этом коэффициенты a, b и c взять из таблицы 1.14.
Таблица 1.14
Тема 3. Решение уравнений 3.1. Решить систему линейных уравнений из таблицы 1.15: Таблица 1.15
3.2. Построить график функции и решить уравнение, используя операторы root, polyroots, solve и блок Given…Find, согласно вариантам из таблицы 1.16: Таблица 1.16
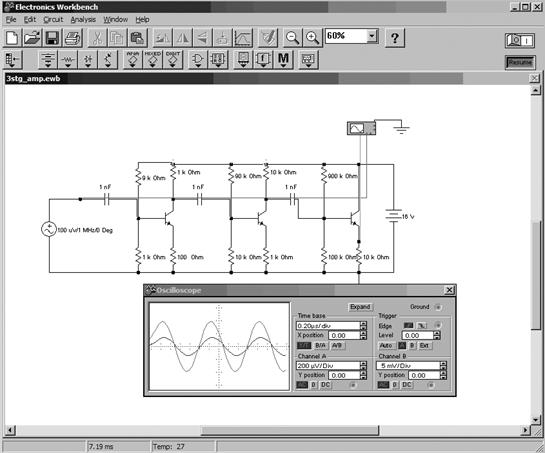
Раздел 2. Имитационное моделирование электронных схем в программе Electronic Workbench (EWB) Тема. Интерфейс и возможности программы Electronic Workbench Общие сведения
Программа Electronic Workbench (EWB) относится к системам схемотехнического моделирования аналоговых и цифровых электронных схем. В данном учебном пособии рассматривается Electronic Workbench 5.12 (EWB 5.12). EWB позволяет моделировать работу схем, включающих пассивные электрические элементы (конденсаторы, индуктивности, резисторы, трансформаторы), диоды, биполярные и полевые транзисторы, логические элементы и т. п. Программа предназначена для схемотехнического моделирования аналоговых и цифровых электронных устройств различного назначения. Окно программы Electronic Workbench (далее по тексту EWB) показано на рисунке 2.1. Составитель должен предупредить пользователя о том, что далеко не все условные графические обозначения (УГО), используемые в библиотеках EWB, совпадают с требованиями российских ГОСТов (как по УГО, так и по шрифтовому исполнению). Поэтому использование собранных в EWB электронных схем возможно только в виде рисунков, а не чертежей. Кроме стандартных Windows-кнопок, на панели инструментов расположены следующие: · поворот; · горизонтальное зеркальное отображение; · вертикальное зеркальное отображение; · создать модель; · вывести график; · свойства компонента; · две кнопки изменения масштаба изображения.
Рис. 2.1. Окно программы EWB Окно программы содержит линейку инструментов с компактным представлением библиотек (рис. 2.2): 1. Sources – источники питания; 2. Basic – группа пассивных компонентов; 3. Diodes – полупроводниковые диоды, стабилитроны и т. п.; 4. Transistors – полупроводниковые транзисторы; 5. Analog ICs – аналоговые микросхемы; 6. Mixed IСs – микросхемы смешанного типа (АЦП, ЦАП); 7. Digital IСs – цифровые микросхемы; 8. Logic Gates – логические цифровые микросхемы. 9. Digital – цифровые микросхемы (отличие от Digital IСs чуть позже); 10. Indicators – индикаторные устройства; 11. Controls – аналоговые вычислительные устройства (дифференциаторы, интеграторы и т.д.); 12. Miscellaneous – компоненты смешанного типа; 13. Instruments – контрольно-измерительные приборы.
Рис. 2.2. Линейка библиотек Рассмотрим подробнее содержимое тех библиотек, которые будут использоваться в лабораторных работах.
Источники питания
В данной библиотеке приведены различного вида источники питания, в том числе и управляемые (рис. 2.3):
Рис. 2.3. Библиотека источников питания 1. Заземление; 2. Батарея (напряжение); 3. Источник постоянного тока (ток); 4. Источник переменного синусоидального напряжения (эффективное значение напряжения, частота, фаза); 5. Источник переменного синусоидального тока (эффективное значение тока, частота, фаза); 6. Источник напряжения, управляемый напряжением (коэффициент передачи); 7. Источник напряжения, управляемый током (коэффициент передачи); 8. Источник тока, управляемый напряжением; 9. Источник тока, управляемый током; 10. Питание ТТЛ-логики; 11. Питание КМОП-логики; 12. Кварцевый генератор; 13. Генератор амплитудно-модулированных сигналов (напряжение и частота несущей, коэффициент и частота модуляции); 14. Генератор фазомодулированных сигналов (напряжение и частота несущей, индекс и частота модуляции).
Пассивные элементы Раздел Basic содержит пассивные элементы (рис. 2.4).
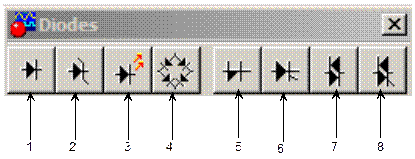
Рис. 2.4. Библиотека пассивных элементов В данный раздел входят следующие опции: 1. Точка ветвления; 2. Резистор; 3. Конденсатор; 4. Катушка (индуктивность); 5. Трансформатор с возможностью редактирования: · коэффициента трансформации; · индуктивности рассеивания; · индуктивности первичной обмотки; · сопротивления первичной обмотки; · сопротивления вторичной обмотки. 6. Электромагнитное реле; 7. Контакт переключающий; 8. Реле времени; 9. Реле напряжения; 10. Реле тока; 11. Резистор напряжения, один конец которого подключен к цепи Vcc (см. «Источники питания»); 12. Потенциометр; 13. Ящик из 8 одинаковых сопротивлений; 14. Переключатель, управляемый напряжением; 15. Электролитический конденсатор; 16. Подстроечный конденсатор; 17. Катушка переменной индуктивности; 18. Элемент для построения моделей индуктивности. Диоды Раздел Диоды содержит полупроводниковые диоды, стабилитроны, динисторы, тринисторы и т. д. (рис. 2.5):
Рис. 2.5. Библиотека диодов 1. Полупроводниковый диод; 2. Стабилитрон; 3. Светодиод; 4. Выпрямительный мост; 5. Диод Шокли; 6. Тиристор; 7. Двуханодный лавинный диод (симметричный динистор); 8. Симистор (симметричный тринистор).
Транзисторы Группа Transistors содержит биполярные и полевые транзисторы (рис. 2.6):
Рис. 2.6. Группа Transistors 1) и 2) – биполярные n–p–n- и p–n–p-транзисторы; 3) n-канальный с управляющим p–n-переходом; 4) p-канальный с управляющим p–n-переходом; 5) трехэлектродный n-канальный с изолированным затвором; 6) трехэлектродный p-канальный с изолированным затвором; 7) четырехэлектродный n-канальный с изолированным затвором; 8) четырехэлектродный p-канальный с изолированным затвором; 9) трехэлектродный n-канальный с обогащенным затвором; 10) трехэлектродный p-канальный с обогащенным затвором; 11) четырехэлектродный n-канальный с обогащенным затвором; 12) четырехэлектродный p-канальный с обогащенным затвором; 13) n-канальный арсенид-галиевый полевой транзистор; 14) p-канальный арсенид-галиевый полевой транзистор. Аналоговые микросхемы В этой библиотеке представлены различные операционные усилители (рис. 2.7):
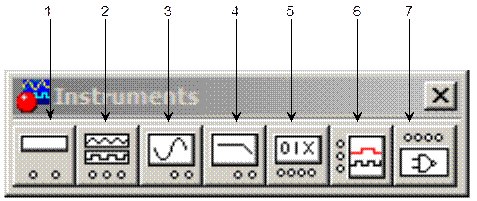
Рис. 2.7. Аналоговые микросхемы 1. Операционный усилитель с фиксированным напряжением питания (линейная модель); 2. Операционный усилитель с изменяемым напряжением питания (нелинейная модель); 3. Операционный усилитель с семью выводами; 4. Операционный усилитель с девятью выводами; 5. Компаратор; 6. Микросхема для системы автоподстройки частоты. Измерительные приборы В этой библиотеке представлены различные измерительные приборы (рис. 2.8): 1. Мультиметр; 2. Функциональный генератор; 3. Осциллограф; 4. Построитель частотных характеристик; 5. Генератор слов.
|
|
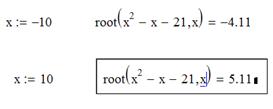

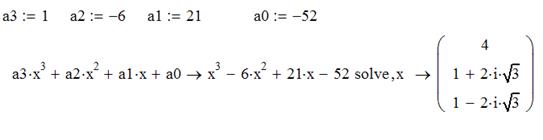
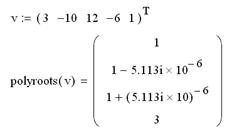



 или y”(x)
или y”(x)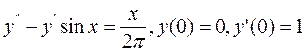




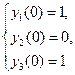

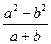
















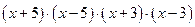

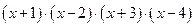



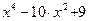
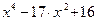





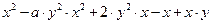





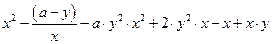

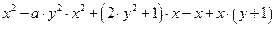


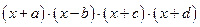
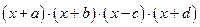


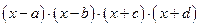

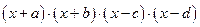






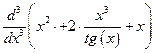


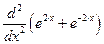
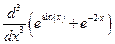
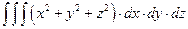



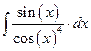


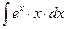

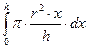
 ,
, 
 ,
, 
 ,
, 
 ,
, 
 ,
, 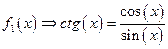
 ,
, 
 ,
,  ,
, 
 ,
, 
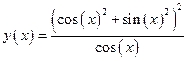 ,
, 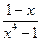


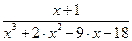

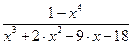




























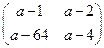





 .
.