|
|
СТАТИЧЕСКИ НЕОПРЕДЕЛИМАЯ СТЕРЖНЕВАЯ СИСТЕМАСОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
М Е Т О Д И Ч Е С К И Е У К А З А Н И Я
к выполнению контрольных работ по сопротивлению материалов для студентов заочной формы обучения строительных специальностей. Часть1. Простые деформации
Брянск 2011
доцент, к.т.н. В.М. Захаров
Рецензент: доцент, к.т.н., зав. кафедрой СК БГИТА С.Г. Парфенов
Рекомендованы учебно-методической комиссией строительного факультета Протокол от
К ЗАДАЧЕ № 1 СТАТИЧЕСКИ НЕОПРЕДЕЛИМАЯ ШАРНИРНО- СТЕРЖНЕВАЯ СИСТЕМА Данные: размеры — а = 2 м; b= 2 м; с =2 м; длины стержней —ℓ1 = 3 м; ℓ2 = 3 м; угол а = 60°; площади поперечных сечений стержней — F1= F2=10 см2=10-3 м2; модули упругости материала стержней — Е1 = Е2 = Е = 2·105 МПа (2·106 кгс/см2). допускаемое напряжение— [σ] = 160 МПа (1600 кгс/см2). Требуется определить величины допускаемых нагрузок Q.двумя способами: по допускаемым напряжениям и по допускаемым нагрузкам. Выражение усилии и напряжений в стержнях через силу Q Задача является один раз статически неопределимой, так как в одно уравнение статики (сумму моментов относительно шарнира А) входят два неизвестных усилия N1 и N2. На рисунке 1.1 показано, что продольные усилия в стержнях N1 и N2 совпадают с реакциями опор rD и rE соответственно. Использование еще двух уравнений статики бесполезно, так как в них неизбежно войдут неизвестные составляющие опорной реакции в шарнире А, не нужные, для решения задачи. Итак, единственное уравнение статики: ∑MA = N1· a · sin α + N2· (a + b) - Q·(a+b+c). (1.1) Для получения дополнительного уравнения необходимо составить уравнение совместности деформаций стержнейΔℓ1 нΔℓ2 (геометрическая сторона задачи) и выразить эти деформации
Рисунок 1.1 через продольные усилия N1 и N2 по закону Гука (физическая сторона задачи). Совместность деформаций Δℓ1 нΔℓ2 может быть установлена непосредственно по чертежу деформированного состоянии системы — рисунок 1,2 (его нужно выполнить с соблюдением масштаба длин). Так как упругие деформации и связанные с ними перемещения точек В и Смалы в сравнении с размерами системы, эти перемещения показаны на рисунке 1.2 не дугами окружностей, образующимися при повороте бруса вокруг точки А,а отрезками, перпендикулярными к прямой ABC. Удлинение стержня 2 равно перемещению точки С, т. е. Δℓ2 =
Рисунок 1.2 Удлинение стержня 1 Δℓ1 = Здесь учтено, что ввиду малости деформаций разность между новой длиной стержня DВ1 и первоначальной DВдопустимо получить, опустив из точки Вперпендикуляр на DВ1. Из подобия треугольников легко получить совместность перемещений точек Ви С:
Разделив (1.3) на (1.2) и учтя (1.4), получаем уравнение совместности деформаций:
По закону Гука:
Подставляя эти выражения в (1.5), имеем:
Дальнейшее решение слишком громоздко выполнять в общем виде. Выполним подстановку числовых значений известных величин, входящих в (1.1) и (1.8), предварительно упростив их сокращениями: N1 ·sin60º + 2N2 =3Q, (1.1') N1 =N2 Совместное решение (1.2') и (1.8') дает
Напряжения в стержнях:
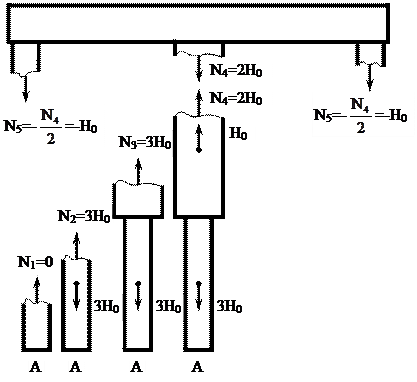
Определение грузоподъемности системы по способу допускаемых напряжений Из условия прочности при растяжении max σ = σ 2 = 0,001262 Q< [σ ] = 160 МПа (1600 кгс/см2), получим QIдоп = Определение грузоподъемности системы по способу допускаемых нагрузок Примем: предел текучести материала — σ т = 240 МПа (2400 кгс/см2), коэффициент запаса прочности — Kт =1,5. Если найденное ранее значение силы QIдоп=126 кН будет превышено в Kт раз, это вызовет текучесть лишь во втором (более напряженном) стержне; Такое состояние принималось за критическое по первому способу. Предельная же грузоподъемность системы Qкт соответствует наступлению состоянии текучести и обоих стержнях. В этом случае усилия в стержнях будут равны: N1т = σт · F1 и N2т = σт · F2 Подставляя эти значения усилий и уравнение равновесия (1.1') имеем: σт · F1 · sin60º + 2 · σт · F2 = 3 · Qкт , откуда Qкт = Допускаемая нагрузка
Сравнение результатов Увеличение допускаемой нагрузки по новому способу расчета
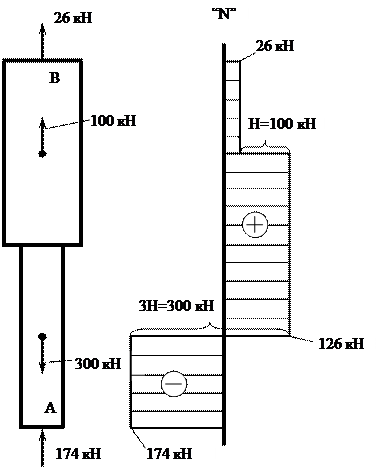
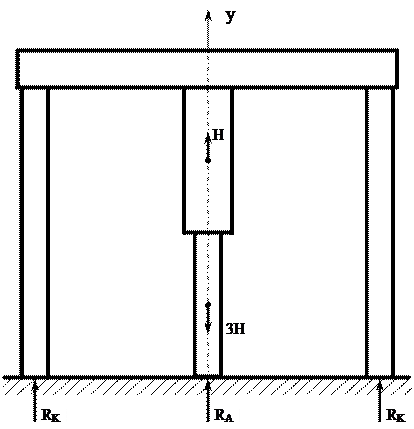
К ЗАДАЧЕ № 2 СТАТИЧЕСКИ НЕОПРЕДЕЛИМАЯ СТЕРЖНЕВАЯ СИСТЕМА Жесткий брус прикреплен к двум стальным стержням с площадью поперечного сечения F, опирающимся на неподвижное основание. К брусу прикреплен средний ступенчатый стальной стержень с зазором Δ= β·С (рисунок 2.1).
Рисунок 2.1
Требуется (без учета собственного веса): 1 Установить, при какой величине сил H0 и 3·H0зазор закроется: 2. Найти реакцию основания в нижнем сечении среднего стержня при заданной величине сил H и 3·H и построить эпюру продольных сил для среднего стержня. 3. Найти усилия и напряжения в крайних стержнях при заданной величине сил H и 3·H. 4 Установить, на сколько 1радусов надо охладить средний стержень, чтобы реакция основания в нижнем сечении среднего стержня при заданной величине сил H и 3·H обратилась в нуль. Примем следующие данные: С = 2,0 м;. F = 20 см2; H = 100 кН (10 тс), β = 5·10-5; Е = 2·105МПа (2·106 кгс/см2); а=12,5·10-6; Δ= β·С = 5·10-5·2,0 = 10-4м = 0,01 см. 2.1. Определение величины сил H0 и 3·H0, при которых зазор закроется Закрытию зазора соответствует перемещение точки Авниз на величину Δ. Это перемещение складывается из перемещения вниз верхней плиты (ΔВ), равного деформации сжатия крайних стержней, и перемещения точки Аотносительно точки В(ΔАВ), равного алгебраической сумме деформаций отдельных участков среднего стержня: Δа = ΔВ + Δав = Δ. (2.1) Запишем выражения для продольных усилий в поперечных сечениях стержней, составляя уравнения равновесия отсеченных частей, показанных на рисунке 2.3. N1(0) = 0; N2(0) = 3·H0; N3(0) = 3·H0; N2(0) = 3·H0; N3(0) = 3·H0.
Рисунок 2.2
По закону Гука: ΔB = │Δℓ5│= ΔAB = Δℓ1 + Δℓ2 + Δℓ3 + Δℓ4 = =0+
Подставляя эти значения перемещений в (2.1), имеем: Δа = ΔВ + Δав = Теперь, используя (2.1), окончательно получаем: H0 = = 8,42 ·103 Н = 8,42 кН (8,42 кН).
2.2. Определение реакции основания в нижнем сечении среднего стержня приH = 100 кН (10 тс) Так как H > H0, то после исчезновения зазора средний стержень упрется в опору, вызвав в ней реакцию RA, направленную вверх. Направление реакций опор в нижних сечениях крайних стержней (RК) предугадать нельзя. Предположим, что они тоже направлены вверх, как показано на рисунок 2.3. Условие равновесия дает: ΣY=RА + 2RК – ЗH + H = 0. (2.3) В это единственное уравнение статики входят два неизвестных. Поэтому задача является один раз статически неопределимой. Дополнительное уравнение получим из условия совместности деформаций, которое можно записать бесчисленным множеством вариантов в соответствии с выбором так называемой основной системы. Основной называется геометрически неизменяемая статически определимая система, получаемая из заданной статически неопределимой системы удалением «лишних» связей. Возьмем в качестве «лишней» связи опору под средним стержнем. На рисунке 2.3 показана такая основная система, загруженная заданными силами H и 3Н и неизвестной реакцией RA,которая должна заменить отброшенную связь.
Рисунок 2.3
Если бы реакции RA не было, то под действием заданных сил нижнее сечение среднего стержня заняло бы положение 1—1, совершив перемещение Δар. Искомая реакция ra. должна быть такой величины, чтобы вызываемая ею деформация системы соответствовала перемещению нижнего сечения среднего стержня вверх до уровня опоры (ΔAX). Из чертежа очевидно следующее уравнение совместности деформаций, записанное в перемещениях точки А: ΔAX = Δар – Δ. (2.4)
Рисунок 2.4
Перемещение точки A вниз от действия заданных сил можно определить по аналогии с тем, как это было сделано в пункте (1) задачи по формуле (2.2): Δар = Перемещение точки А вверх от действия силы RAскладывается из укорочения среднего стержня, во всех сечениях которого возникает сжимающая продольная сила, равная RAи растяжения крайних стержней, в каждом из которых возникает продольная сила, равная 0,5 RA. Используя закон Гука, имеем: ΔAX = = + Подставляем эти значения перемещений в (2.4) и, учитывая, что Δ= β·С = 5·10-5·2,0 = 10-4м = 0,01 см., имеем: 1,25 откуда: RA = =174·103 Н = 174 кН (17,4 тс). Статическая неопределимость раскрыта: RA = 174 кН (17,4 тс). Продольные усилия в поперечных сечениях на отдельных участках среднего стержня получим, составляя алгебраические суммы внешних сил, расположенных ниже этих поперечных сечений: N1 = –RA = –174 кН (17,4 тс); N2 = N3 = –RA + 3H = –174 + 3·100 = 126 кН (12,6 тс); N4 = –RA + 3H – H = –174 + 3·100 – 100 = 26 кН (2,6 тс); По этим данным строим эпюру продольных сил для среднего стержня (рисунок 2.5).
Рисунок 2.5 |
|

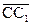 . (1.2)
. (1.2)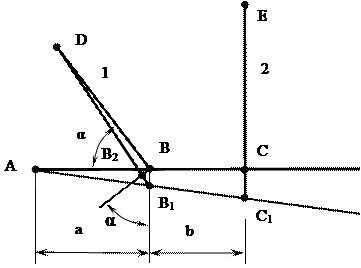
 =
= 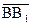 · sin α . (1.3)
· sin α . (1.3)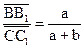 : (1.4)
: (1.4)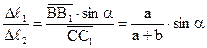 (1.5)
(1.5) . (1.6)
. (1.6) . (1.7)
. (1.7)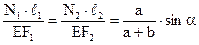 . (1.8)
. (1.8) sin60º . (1.8')
sin60º . (1.8')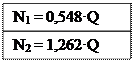
 = 548 Q Па =0,000548 Q МПа (0,0548 Q кгс/см2)
= 548 Q Па =0,000548 Q МПа (0,0548 Q кгс/см2) = 1262 Q Па =0,001262 Q МПа (0,1262 Q кгс/см2)
= 1262 Q Па =0,001262 Q МПа (0,1262 Q кгс/см2)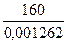 =126000 Н = 126 кН (12,6 тс)
=126000 Н = 126 кН (12,6 тс)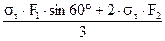 =
= 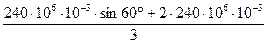 = 230000 Н= 230 кН (23000 кгс).
= 230000 Н= 230 кН (23000 кгс).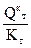 =
=  = 153 кН (15300 кгс, 15,3 тс).
= 153 кН (15300 кгс, 15,3 тс).
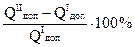 =
=  =21,5%
=21,5%




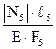 =
= 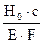 ;
; +
+  +
+ 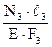 +
+  =
=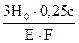 +
+ 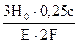 +
+ 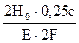 =
= 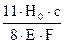
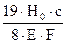 (2.2)
(2.2) =
= 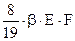 =
= 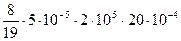 =
=


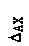

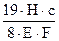 =
= 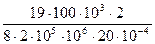 = 1,19·10-3 м = 0,119 cм
= 1,19·10-3 м = 0,119 cм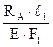 +
+ 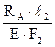 +
+  +
+  +
+ 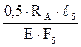 =
= +
+  +
+ 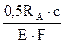 = 1,25
= 1,25 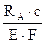
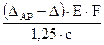 =
=  =
=