|
|
ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ТЕЛМЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ Цель работы: ознакомиться с одним из методов экспериментального определения моментов инерции тел относительно произвольных осей вращения. Приборы и принадлежности: прибор для определения моментов инерции тел, исследуемые тела, секундомер. ВВЕДЕНИЕ
Прочтите введение к работам №3 и №4 данных методических указаний. Как видно из определения, момент инерции тела, как и масса, есть величина аддитивная: момент инерции тела равен сумме моментов инерции его частей; момент инерции системы тел равен сумме моментов инерции отдельных тел. Момент инерции тела зависит не только от его массы, но и от распределения массы относительно оси вращения. Если момент инерции тела относительно оси, проходящей через центр масс, равен, то, согласно теореме Штейнера, момент инерции I относительно оси, параллельной данной и находящейся на расстоянии d от нее, можно найти по формуле:
Имеется много методов экспериментального определения моментов инерции тел. В настоящей работе используется метод крутильных (вращательных) колебаний.
ОПИСАНИЕ УСТАНОВКИ И МЕТОДА ИЗМЕРЕНИЯ
Рис. 5.1.
Установка (рис. 5.1.) состоит из станины 1 с укрепленной на ней вертикальной стойкой 2 с кронштейном 3. К кронштейну на стальной проволоке подвешена на рамке круглая платформа 4. По окружности платформы могут перемещаться грузы 5. С помощью этих грузов приводится в центр платформы центр тяжести системы: платформа – исследуемые тела, что проверяется по совпадению указателей наконечников –7, закрепленных на верхней стороне основания прибора 6 и на нижней стороне платформы 4. Благодаря упругим свойствам стальной проволоки платформа, после закручивания на некоторый угол j, будет совершать вращательные (крутильные) колебания. На платформе начерчены концентрические окружности через 10 мм для точного расположения исследуемого тела относительно оси вращения. К установке прилагается эталонное тело с известным моментом инерции относительно его главной оси симметрии. Если повернуть платформу на угол j от положения равновесия, то со стороны стальной проволоки на нее будет действовать противодействующий момент сил, пропорциональный (в пределах упругой деформации ) углу j
где к – коэффициент упругости (жесткость) пружины. Уравнение движения платформы будет иметь вид
где
Решение этого дифференциального уравнения второго порядка имеет вид
где j0 – амплитуда колебаний, w - круговая частота, a - начальная фаза. Круговая частота w и период колебаний Т связаны между собой соотношением
и зависят от параметров системы: момента инерции и упругости
Для определения момента инерции тела, его устанавливают на платформе и определяют период колебаний, измеряя время t совершения колебания n колебаний:
А с другой стороны
где I0 – момент инерции ненагруженного диска. Зная I0 и К легко найти I. Для определения I0 используют эталонное тело с известным моментом инерции относительно его центральной оси. Iэт. Измерив периоды колебаний ненагруженной платформы Т и период колебаний с эталонным телом Тэт получим систему уравнений:
Решая их относительно К и I0 имеем
Расположив на платформе вместо эталонного тела исследуемое, получим аналогичным образом
где I – момент инерции системы: исследуемое тело-платформа; I1 – момент инерции исследуемого тела; Т1 – период колебаний системы, отсюда
Если Т1 мало отличается от Т0 уравнение (5.4.) упрощается:
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Для нормальной работы установки необходимо предварительно юстировать ее. Указатели 7 должны быть строго друг против друга. Этого добиваются передвижением грузов 5. 2. Определить период колебаний ненагруженной платформы. Для этого повернуть ее на угол 90-1000 и отпустить, предоставив возможность свободного колебания платформы. Измерить время колебаний и определить период по уравнению (5.1.) 3. Поместить эталонное тело в центр платформы и определить период колебаний данной системы, подобно п.2. 4. Рассчитать по уравнению (5.2.) момент инерции, а по уравнению (5.3.) коэффициент упругости стальной проволоки. 5. По заданию преподавателя определить момент инерции тела. Для этого установить исследуемое тело на платформу. Определить период колебаний системы с исследуемым телом. Рассчитать момент инерции тела по уравнению (5.4.) или (5.5.). 6. Определить момент инерции того же тела относительно другой оси, параллельной данной. 7. Проверить теорему Штейнера. 8. Данные измерений занести в таблицу:
Таблица 5.1. |
|


 ,
,

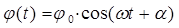

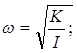


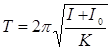


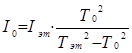 (5.2.)
(5.2.)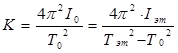 (5.3.)
(5.3.)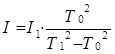
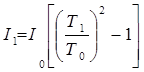 (5.4.)
(5.4.) (5.5.)
(5.5.)