|
|
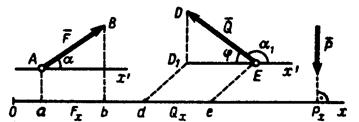
Разложение силы на сходящиеся составляющиеРазложить данную силу на две или несколько сходящихся составляющих сил значит найти такую систему двух или нескольких сходящихся сил, для которой данная сила является равнодействующей. Эта задача является неопределённой и имеет однозначное решение лишь при задании дополнительных условий. Рассмотрим два частных случая: Разложение силы по двум заданным направлениям. По данной силе Такими дополнительными условиями могут, например, быть: 1) задание двух направлений, по которым должны действовать составляющие; 2) задание модулей обеих составляющих сил; 3) задание модуля одной составляющей силы и направление другой. В первом случае задача сводится к построению такого параллелограмма, у которого диагональ будет изображать силу Два последних случая предоставляем читателю рассмотреть самостоятельно. Разложение силы по трем заданным направлениям. Исходя из правила параллелепипеда сил, можно решить задачу о разложении данной силы Проекция силы на ось и на плоскость. Аналитический способ задания и сложения сил Проекция силы (как и любого другого вектора) на ось есть алгебраическая величина, равная произведению модуля силы на косинус угла между силой и положительным направлением оси. Если этот угол острый, - проекция положительна, если тупой, - отрицательна, а если сила перпендикулярна оси, - её проекция на ось равна нулю. Так, для сил, изображённых на рис. 1.17
Рисунок 1.17 – Проекции силы на ось Проекцию силы на ось будем обозначать той же буквой, которой обозначена сила, но со знаком внизу, указывающим наименование оси проекций (например, Проекцией силы
где Заметим, что для нахождения проекции силы
Аналитический способ задания сил.Для аналитического задания силы необходимо выбрать систему координатных осей Oxyz, по отношению к которой будет определяться направление силы в пространстве. В механике пользуются правой системой координат, в которой кратчайшее совмещение оси Ox с осью Oy происходит, если смотреть с положительного конца оси Oz, против хода часовой стрелки (рисунок 1.18).
Вектор, изображающий силу Для решения задач механики удобнее задавать силу её проекциями
Если все рассматриваемые силы расположены в одной плоскости Oxy
Аналитический способ сложения сил. Переход от зависимостей между векторами к зависимостям между их проекциями осуществляется с помощью следующей теоремы геометрии: проекция вектора суммы на какую-нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось. Согласно этой теореме, если
Зная Rx, Ry, Rz, по формулам 1.9 находим:
Произвольная система сил |
|
 , очевидно, можно построить бесчисленное множество параллелограммов сил, и, следовательно, задача о разложении данной силы на две сходящиеся составляющие силы является в такой постановке неопределенной и имеет однозначное решение лишь при задании двух дополнительных условий.
, очевидно, можно построить бесчисленное множество параллелограммов сил, и, следовательно, задача о разложении данной силы на две сходящиеся составляющие силы является в такой постановке неопределенной и имеет однозначное решение лишь при задании двух дополнительных условий. ,
,  ,
,  .
.
 и
и  , или прописной буквой
, или прописной буквой 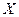 и
и  ).
).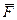 на плоскость Oxy называется вектор
на плоскость Oxy называется вектор  , заключённый между проекциями начала и конца силы
, заключённый между проекциями начала и конца силы  на эту плоскость (Рисунок 1.18). По модулю
на эту плоскость (Рисунок 1.18). По модулю ,
,
 - угол между направлением силы
- угол между направлением силы  .
. , например на ось х, можно сначала найти ее проекцию на плоскость Oxy, в которой эта ось лежит, а затем найденную проекцию на плоскость
, например на ось х, можно сначала найти ее проекцию на плоскость Oxy, в которой эта ось лежит, а затем найденную проекцию на плоскость  . спроектировать на данную ось:
. спроектировать на данную ось: ,
,


 ,
,  ,
,  , на три прямоугольные декартовы оси координат Ох, Оу и Оz (рисунок 1.18). Зная эти проекции, можно определить модуль силы и углы, которые она образует с координатными осями, по формулам:
, на три прямоугольные декартовы оси координат Ох, Оу и Оz (рисунок 1.18). Зная эти проекции, можно определить модуль силы и углы, которые она образует с координатными осями, по формулам: ;
;
 ,
,  ,
,  .
.
 ;
;
 ,
,  ,
,  , …
, …  , т.е.
, т.е.  , то
, то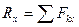 ,
,  ,
,  .
.
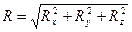 ;
;
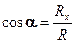 ,
,  ,
,  .
.