|
|
Количество движения и кинетическая энергия точки. Импульс силыКоличество движения и кинетическая энергия являются основными динамическими характеристиками движения точки. Количеством движения материальной точки называется векторная величина Кинетической энергией материальной точки называется скалярная величина Элементарным импульсом силы Полный импульс силы за некоторый конечный промежуток времени будет
В проекциях на оси координат:
Если В проекциях на оси координат: Если к точке приложено несколько сил
В проекциях на оси координат:
Теорема об изменении количества движения точки. Пусть точка М массы m движется под действием сил
Так как
Равенство (3.13) выражает теорему об изменении количества движения точки в дифференциальной форме: производная по времени от количества движения точки равна геометрической сумме всех действующих на точку сил. Пусть в момент времени t=0 скорость точки
Так как
Равенство (3.14) выражает теорему об изменении количества движения точки в конечном виде: изменение количества движения точки за некоторый конечный промежуток времени равно геометрической сумме импульсов всех действующих на точку за тот же промежуток времени в проекциях на оси координат:
Теорема об изменении количества движения точки в основном применяется на тех участках траектории движения точки, на которых задано время движения точки или это время нужно определить.
Момент количества движения точки относительно центра и оси. Теорема об изменении момента количества движения точки (теорема моментов) В некоторых задачах в качестве динамической характеристики движения точки вместо самого вектора количества движения
Рис. 3.4
Эти моменты определяются так же, как и моменты силы в статике. Таким образом, моментом количества движения точки относительно некоторого центра О называется векторная величина
где r – радиус – вектор движущейся точки М, проведенный из центра О. Вектор Момент количества движения точки относительно какой-нибудь оси
где Теорема моментов устанавливает, как изменится со временем вектор Но Следовательно,
Равенство (3.16) выражает теорему моментов относительно центра: производная по времени от момента количества движения точки, взятого относительно какого-нибудь неподвижного центра равна моменту действующей на точку силы относительно того же центра. Проецируя равенство (3.16) на какую-нибудь ось Равенство (3.5) выражает теорему моментов относительно оси Из равенства (3.4) следует, что если
Работа силы. Мощность Элементарной работой силы (Здесь dA – символ элементарной величины, но не дифференциала. Дифференциалом какой-нибудь функции величина dA вообще может не быть.)
Так как
Если учесть, что
Следовательно, элементарная работа силы равна скалярному произведению силы на вектор элементарного перемещения ее точки приложения. Через проекции векторов Работа силы на любом конечном перемещении
или
Если Мощность. Мощностью называется величина, характеризующая быстроту совершения работы силой и равная отношению элементарной работы к промежутку времени, за который она совершена. (Определяющая работу, совершаемую силой в единицу времени). Если работа совершается равномерно, то мощность В общем случае
|
|

 , равная произведению массы точки на ее скорость. Вектор
, равная произведению массы точки на ее скорость. Вектор  , равная половине произведения массы точки на квадрат ее скорости.
, равная половине произведения массы точки на квадрат ее скорости.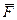 называется векторная величина
называется векторная величина  , равная произведению силы
, равная произведению силы 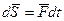
 .
.
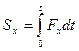 ,
,  ,
,  .
.
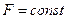 , то
, то  или
или 
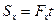 ,
,  ,
, 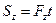
 то их равнодействующая
то их равнодействующая  . Умножим обе части этого равенства на
. Умножим обе части этого равенства на 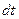 и проинтегрируем
и проинтегрируем , откуда
, откуда 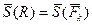 , т.е импульс равнодействующей равен геометрической сумме импульсов всех равнодействующих на точку сил.
, т.е импульс равнодействующей равен геометрической сумме импульсов всех равнодействующих на точку сил.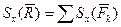 ,
,
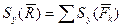 ,
,
 .
.
 (рисунок 3.1). Запишем для данной точки основное уравнение динамики (3.2)
(рисунок 3.1). Запишем для данной точки основное уравнение динамики (3.2)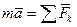
 ,
,  то основное уравнение динамики запишется в виде:
то основное уравнение динамики запишется в виде:
 , а в момент времени t скорость точки
, а в момент времени t скорость точки  . Разделяя переменные в равенстве и интегрируя, получим:
. Разделяя переменные в равенстве и интегрируя, получим: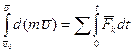
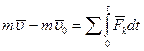
 , геометрической сумме импульсов сил
, геометрической сумме импульсов сил  , то
, то
 ;
; ;
; .
. рассматривают его момент относительно некоторого центра или оси.
рассматривают его момент относительно некоторого центра или оси.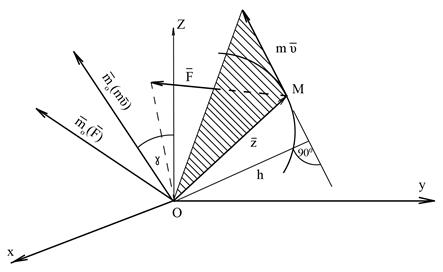
 , определяемая равенством:
, определяемая равенством:
 (рис. 3.4: для сравнения на нем показан и вектор
(рис. 3.4: для сравнения на нем показан и вектор  , который перпендикулярен плоскости, проходящей через
, который перпендикулярен плоскости, проходящей через  и центр О)
и центр О) , проходящей через центр О, будет равен проекции вектора
, проходящей через центр О, будет равен проекции вектора 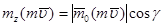 ,
, – угол между вектором
– угол между вектором 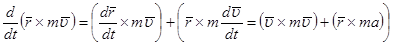
 как векторное произведение двух параллельных векторов, а
как векторное произведение двух параллельных векторов, а 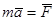
 или
или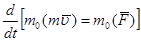
 .
. , то
, то 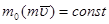
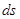 называется скалярная величина
называется скалярная величина  (рис. 3.5)
(рис. 3.5)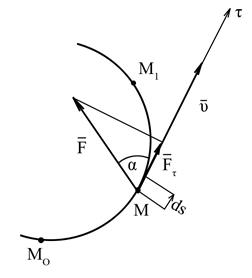 Рис. 3.5
Рис. 3.5 , то
, то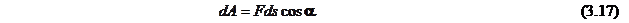
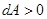 , если сила
, если сила  способствует движению точки
способствует движению точки  - острый.
- острый. , если сила
, если сила  препятствует движению точки
препятствует движению точки  - тупой.
- тупой. , если
, если 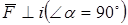
 , где
, где  - вектор элементарного перемещения точки М и воспользоваться известным из векторной алгебры понятием о скалярном произведении двух векторов, то равенство (3.17) можно записать в виде
- вектор элементарного перемещения точки М и воспользоваться известным из векторной алгебры понятием о скалярном произведении двух векторов, то равенство (3.17) можно записать в виде
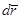 на координатные оси равенство (3.18) запишется в виде
на координатные оси равенство (3.18) запишется в виде 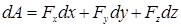 – аналитическое выражение элементарной работы.
– аналитическое выражение элементарной работы. будет равна
будет равна

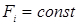 , то
, то 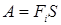 , где
, где  .
.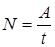 , где
, где  – время, в течении которого совершена работа А
– время, в течении которого совершена работа А .
.