|
|
Молекулярная физика и термодинамикаОсновные формулы
Количество вещества тела (системы) ν = N / NA, где N – число структурных элементов (молекул, атомов, ионов и т. п.), составляющих тело (систему); NA – постоянная Авогадро (NA= 6,02·1023 моль-1). Молярная масса вещества μ = m / ν, где m – масса однородного тела (системы); ν – количество вещества этого тела. Количество вещества смеси газов ν = ν1 + ν2 + ... + νn = N1 / NA + N2 / NA + ... + Nn / NA, или ν = m1 / μ1 + m2 / μ2 + ... + mn / μn, где νi, Ni, mi, μi – количество вещества, число молекул, масса, молярная масса i-го компонента смеси соответственно. Уравнение Менделеева-Клапейрона (уравнение состояния идеального газа) pV = νRT = где m – масса газа; μ – молярная масса газа; R – молярная газовая постоянная; ν – количество вещества; T – термодинамическая температура. Опытные газовые законы, являющиеся частными случаями уравнения Менделеева-Клапейрона для изопроцессов: а) закон Бойля-Мариотта (изотермический процесс T = const, m = const) pV = const,
или для двух состояний газа
p1V1 = p2V2;
б) закон Гей-Люссака (изобарный процесс: p = const, m = const):
или для двух состояний газа
в) закон Шарля (изохорный процесс: V = const, m = const):
или для двух состояний
г) объединенный газовый закон (m = const):
где p1,V1, T1 и p2, V2, T2 – давление, объем и температура газа в начальном и конечном состояниях, соответственно. Закон Дальтона, определяющий давление смеси газов:
p = p1 + p2 +...+ pn,
где pi – парциальные давления компонентов смеси; n – число компонентов смеси. Парциальным давлением называется давление газа, которое производил бы этот газ, если бы только он один находился в сосуде, занятом смесью. Молярная масса смеси газов
μ=
где mi – масса i-го компонента смеси; νi – количество вещества i-го компонента смеси, νi = mi / μi; n – число компонентов смеси. Массовая доля i-го компонента смеси газа (в долях или процентах)
ωi = mi / m,
где m – масса смеси. Концентрация молекул
n =
где N – число молекул, содержащихся в данной системе; ρ – плотность вещества; V – объем системы. Формула справедлива не только для газов, но и для любого агрегатного состояния вещества. Основное уравнение кинетической теории газов
p = 2/3n
где Средняя кинетическая энергия поступательного движения молекулы
где k – постоянная Больцмана. Средняя полная кинетическая энергия молекулы
где i – число степеней свободы молекулы. Зависимость давления газа от концентрации молекул и температуры:
p = nkT. Скорости молекул:
где m1 – масса одной молекулы. Относительная скорость молекулы
u = V/Vв,
где V – скорость данной молекулы. Среднее число столкновений молекулы газа за 1 с
где d – эффективный диаметр молекулы газа; n –концентрация молекул газа;
Средняя длина свободного пробега молекул (расстояние, проходимое молекулой газа между двумя последовательными столкновениями)
Удельные теплоемкости газа при постоянном объеме Cv и постоянном давлении Cp
Cv =
Связь между удельной c и молярной C теплоемкостями:
C = C / μ, С = сμ. Уравнение Майера Cp – Cv = R. Внутренняя энергия идеального газа U = Первое начало термодинамики
Q =
где Q – теплота, сообщенная системе (газу);
A – работа, совершенная системой против внешних сил. Работа расширения газа: A = A = p (V2 – V1) – при изобарном процессе; A =
A = - где γ – показатель адиабаты, γ = CP/CV. Уравнение Пуассона, связывающее параметры идеального газа при адиабатном процессе,
pV γ = const;
Коэффициент полезного действия (КПД) цикла
η=
где Q1 – теплота, полученная рабочим телом от нагревателя; Q2 – теплота, переданная рабочим телом холодильнику. КПД цикла Карно
η = где T1 и T2 – температуры нагревателя и холодильника. Разность энтропий двух состояний B и A определяется формулой
Примеры решения задач Пример 1.Определить: 1) число N молекул воды, занимающей при температуре t = 4oC объем V = 1мм3 = 10-9м3; 2) массу m1 молекулы воды.
Так как Так как Вычисляем:
2) Массу одной молекулы воды найдем делением ее молярной массы на постоянную Авогадро:
Пример 2. Определить: 1) среднюю кинетическую энергию движения одной молекулы кислорода при температуре Т = 286К; 2) среднюю кинетическую энергию <εвр> и среднюю кинетическую энергию <εп> поступательного движения одной молекулы; 3) кинетическую энергию движения всех молекул W; 4) кинетическую энергию Wвр вращательного движения всех молекул; 5) кинетическую энергию поступательного движения всех молекул. Масса кислорода m = 4 г = 4·10-3кг.
является двухатомной, а следовательно, обладает степенями свободы, средняя кинетическая энергия одной молекулы:
2) Средняя кинетическая энергия вращательного движения и поступательного движения одной молекулы соответственно:
Соответственно:
3) Средняя кинетическая энергия всех движения всех молекул выразится соотношением
где М = 32·10-3кг/моль – молярная масса, то:
4) 5)
Пример 3. Средняя длина свободного пробега
2) средняя квадратичная скорость:
3) наиболее вероятная скорость:
4) среднее число соударений в 1с определяется отношением средней арифметической скорости
Пример 4.В баллоне объемом V = 10 л = 10·10-3 м3 находится гелий под давлением Р1 = 1МПа = 106 Па при температуре Т1 = 300 К. После того, как из баллона был израсходован гелий массой ∆m = 10 г = 10·10-3кг, температура в баллоне понизилась до Т2 = 290К. Определить: 1) давление Р2 гелия, оставшегося в баллоне; 2) массу гелия в баллоне в начальном и конечном состояниях; 3) плотность гелия до и после расходования.
где R = 8,31 Дж/моль·К – газовая постоянная, М = 4·10-3 кг/моль – молярная масса. Выразим массы m1 и m2 в начальном и конечном состояниях:
Вычитая будем иметь:
Отсюда найдем искомое давление:
Вычисляем:
2) Масса гелия в начальном и конечном состояниях соответственно:
Иначе:
3) Плотность гелия в баллоне в начальном и конечном состояниях:
Пример 5. Найти среднюю кинетическую энергию
Так как молекула кислорода двухатомная, то число степеней свободы
|
|
 RT,
RT,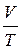 = const,
= const, ;
; = const,
= const, ;
; = const, или
= const, или  ,
, ,
, =
=  ,
, ,
, – средняя кинетическая энергия поступательного движения молекулы.
– средняя кинетическая энергия поступательного движения молекулы. = 3/2 kT,
= 3/2 kT, =
=  kT,
kT, – средняя квадратичная;
– средняя квадратичная; – средняя арифметическая;
– средняя арифметическая; – наиболее вероятная,
– наиболее вероятная, ,
, – средняя арифметическая скорость молекул газа.
– средняя арифметическая скорость молекул газа. .
. ; Cp =
; Cp =  .
. .
. U + A,
U + A, – в общем случае;
– в общем случае; RT ln
RT ln  – при изотермическом процессе;
– при изотермическом процессе; CV
CV  T, или A =
T, или A =  – при адиабатном процессе,
– при адиабатном процессе, ;
; ;
;  .
. ,
,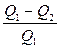 =
=  ,
, S=
S=  .
.
 , где М = 18·10-3кг/моль – молярная масса, то
, где М = 18·10-3кг/моль – молярная масса, то  .
. , где ρ = 103кг/м3 – плотность воды, то
, где ρ = 103кг/м3 – плотность воды, то 
 .
. .
. , где
, где  -
-
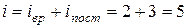


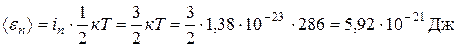

 ;
; .
. , если учесть, что число всех молекул
, если учесть, что число всех молекул ,
, .
.

 .
. молекулы углекислого газа при нормальных условиях(Т = 273К; Р=105Па) равна
молекулы углекислого газа при нормальных условиях(Т = 273К; Р=105Па) равна  ,
где
,
где  - молярная масса.
- молярная масса.



 к средней длине свободного пробега:
к средней длине свободного пробега:
 ;
; 
 ;
;  .
.

 .
.

 .
.

 движения одной молекулы кислорода при Т = 350 К , а также кинетическую энергию движения всех молекул кислорода массой m = 4 г = 4·10-3кг.
движения одной молекулы кислорода при Т = 350 К , а также кинетическую энергию движения всех молекул кислорода массой m = 4 г = 4·10-3кг. , где k = 1,38·10-23Дж/к – постоянная Больцмана; Т – термодинамическая температура.
, где k = 1,38·10-23Дж/к – постоянная Больцмана; Т – термодинамическая температура.
 ‑?
‑?
