|
|
Описание установки и метода измерений
Устройство установки показано на рис. 1. Основание 1 оснащено регулируемыми ножками 2, которые позволяют произвести выравнивание прибора. В основании закреплена колонка 3, к ней прикреплены неподвижный верхний кронштейн 4 и подвижный кронштейн 5. На верхнем кронштейне находятся электромагнит 6, фотоэлектрический датчик 7 и винт для закрепления и регулирования длины подвеса маятника. Нижний кронштейн вместе с прикрепленным к нему фотоэлектрическим датчиком 9 можно перемещать вдоль колонки и фиксировать в произвольно выбранном положении. Маятник Максвелла представляет собой диск 11, закрепленный на оси 10. Ось подвешена на двух нитях 12. На диске можно закреплять различные кольца, изменяя этим момент инерции системы. Длину маятника можно определить по миллиметровой шкале 13 на колонке прибора. Для этого на нижнем кронштейне есть указатель, который помещен на высоте светового луча нижнего фотоэлектрического датчика. Маятник удерживается в верхнем положении электромагнитом. Нажатием кнопки "ПУСК" отключается электромагнит и включается электросекундомер 14. Электросекундомер отключается, как только опускающийся маятник перекроет световой поток, падающий на нижний фоторезистор. В данной работе определяют момент инерции маятника Максвелла. Для вывода расчетной формулы применим закон сохранения энергии, считая движущийся маятник консервативной системой. Наматывая на ось маятника нить подвеса, поднимем его на высоту h. При этом маятник приобретет потенциальную энергию П = mgh, где m - масса маятника. При раскручивании нити опускающийся маятник движется поступательно и одновременно вращается вокруг своей оси. При этом потенциальная энергия маятника превращается в кинетическую энергию. По закону сохранения энергии для момента времени, когда маятник опустится с высоты h, имеем
где u - скорость поступательного движения маятника; J - момент инерции маятника относительно своей оси; w - угловая скорость вращения маятника. Так как равноускоренное движение маятника начинается из состояния покоя, то
где t - время опускания маятника с высоты h. Тогда
Угловая скорость вращающегося маятника связана с линейной скоростью точек боковой поверхности оси соотношением
где Do - диаметр оси маятника. Подставляя (2) в (3), получим
Заменив в соотношении (1) u и w выражениями (2) и (4), получим выражение для момента инерции маятника
Для нашей установки
Таким образом, для определения момента инерции маятника Максвелла нужно измерить величины m, D, h, t.
Порядок выполнения работы
1. На диске маятника укрепить произвольно выбранное кольцо. 2. Произвести корректировку установки маятника, обращая внимание на то, чтобы его ось была параллельна основанию прибора. 3. Включить прибор в сеть. Таблица 1
4. Нажать клавишу "СЕТЬ". Проверить, все ли индикаторы измерителя высвечивают цифру "нуль", и засветились ли лампочки обоих фотоэлектрических датчиков. 5. Отжать кнопку "ПУСК" электросекундомера. 6. Намотать на ось маятника нить подвеса, обращая внимание на то, чтобы она наматывалась равномерно, виток к витку. 7. Зафиксировать маятник в верхнем положении при помощи электромагнита (клавиша пуск должна быть отжата). 8. Нажать кнопку "СБРОС". 9. Нажать кнопку "ПУСК". 10. Результаты измерений записать в табл. 1. 11. По вертикальной колонке определить длину маятника, равную высоте h, с которой он опускается. 12. Вычислить массу маятника по формуле:
где m0, mд, mk - массы оси маятника, диска и кольца, указанные на соответствующих элементах. 13. По формуле (6) вычислить момент инерции маятника, подставляя среднее значение времени <t>. 14. Вычислить относительную погрешность
подставляя сюда <t>. Погрешность измерения времени вычислить по формуле случайной абсолютной ошибки при прямых многократных измерениях для надежности a = 0,95. Ошибкой (g) пренебречь (взять g = 9.81). 15. Вычислить абсолютную погрешность
Результат записать в виде
с надежностью α = … и относительной погрешностью ε = …. 16. Сравнить полученное в опыте значение момента инерции маятника с теоретическим значением Jт, вычисленным по формуле
Значения отдельных моментов инерции вычислить по формулам
Здесь
Контрольные вопросы
1. Что называется моментом инерции материальной точки относительно точки и относительно оси вращения? Какую роль он играет во вращательном движении? 2. Как вычислить момент инерции сплошного тела? От чего зависит момент инерции тела? 2. Что называется моментом силы относительно точки, неподвижной оси? Как определить направление момента силы ? 3. Дать определение угловой скорости и углового ускорения. Как определить их направления? 4. Какова связь между линейными и угловыми скоростями и ускорениями? 5. Сформулируйте основной закон динамики вращательного движения. 6. Сформулируйте закон сохранения механической энергии. 7. С каким фундаментальным свойством симметрии времени связан закон сохранения механической энергии. 8. Вывести формулу кинетической энергии вращающегося тела и тела движущегося поступательно. 9. Вывести расчетную формулу (5) и формулы (7). Библиографический список
1.Трофимова, Т. И. Курс физики / Трофимова Т.И. – М.: Академия, 2004. – § 16–18. 2. Савельев, И. В. Курс общей физики в 3-х т. Т.1 / И. В. Савельев.– СПб.: Лань, 2005. – § 19–24, 39,41. 3. Кингсеп, А. С. Основы физики: в 2-х т. Т. 1 / А. С. Кингсеп, Г. Р. Локшин, О. А. Ольхов. – М.: Физматлит, 2001. – Гл.7 § 7.1, 7.3, 7.4, 7.6. 4. Сивухин, Д.В. Общий курс физики: в 5-ти т. Т.1 / Д. В. Сивухин. – М.: Физматлит МФТИ, 2005. – § 30, 32–38. 5. Курс физики: Учебник для вузов: в 2-х т. Т. 1 / Под ред. В. Н. Лозовского. – СПб.: Лань, 2006. – Гл. 1.6 § 1.33, 1.34.
ЛАБОРАТОРНАЯ РАБОТА № 8. |
|
 Рис. 1
Рис. 1
 , (1)
, (1) ,
,  ,
, . (2)
. (2) , (3)
, (3)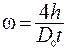 . (4)
. (4) . (5)
. (5) , с учетом этого неравенства выражение (5) примет вид
, с учетом этого неравенства выражение (5) примет вид . (6)
. (6) ,
,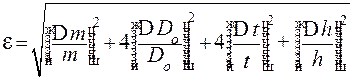 .
.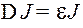 .
. , кг·м2
, кг·м2 .
. ,
, , (7)
, (7) .
.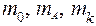 - массы оси маятника, диска и кольца;
- массы оси маятника, диска и кольца; - внешние диаметры оси маятника, диска и кольца.
- внешние диаметры оси маятника, диска и кольца.