|
|
Тема: «Теория относительности»Инвариантность и относительность величин. В практике движение одного и того же тела рассматривают в разных системах отсчета, при этом кинематические характеристики движения при переходе из одной системы отсчета в другую могут изменяться или оставаться одинаковыми. Характеристики, имеющие одинаковые значения в разных системах отсчета, называют инвариантными. К инвариантным величинам относятся промежуток времени, длина отрезка, стержня и т. и. Вывод об инвариантности этих величин сделан на основе обобщения опыта. В своей непосредственной практике человек чаще всего встречается с движением тел, скорости которых много меньше скорости света, поэтому вывод об инвариантности промежутков времени и отрезков в различных системах отсчета экспериментально проверен лишь для таких скоростей. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными. Относительными величинами в кинематике являются координаты, перемещение, скорость, а иногда и ускорение. Относительна и траектория движущейся материальной точки. С изменением вида траектории при переходе из одной системы отсчета в другую мы встречаемся в ряде задач. Астрономы, например, хорошо знают, что такие планеты, как Марс, Сатурн, Юпитер, «выписывают» на небе сложные траектории с петлями. Между тем траектории их движения относительно Солнца — эллипсы. Все дело, оказывается, в том, что мы наблюдаем эти планеты в системе отсчета, связанной с Землей, которая сама движется по эллипсу относительно Солнца. Относительность вида траектории можно продемонстрировать и в лаборатории. Отметим на ободе колеса тележки точку и будем наблюдать за ее перемещением при движении тележки. Ясно, что в системе отсчета, связанной с тележкой, траекторией точки будет окружность. В системе отсчета, связанной с Землей, траектория точки будет довольно сложной кривой. Эту кривую называют циклоидой. С точки зрения кинематики все системы отсчета одинаково пригодны для описания движения тел. Это утверждение следует понимать в том смысле, что любое механическое явление можно описать в любой системе отсчета и при этом нет оснований отдавать предпочтение какой-либо одной системе отсчета перед другой. Ни одна из систем отсчета не является «истинной», «настоящей», выбор каждой из систем отсчета определяется лишь соображениями удобства, целесообразности.По значениям кинематических величин в одной системе отсчета можно рассчитывать значения этих же величин в любой другой системе отсчета. Классический закон сложения скоростей.
В случае, когда одна система отсчета движется относительно другой с постоянной скоростью v0, это выражение принимает вид: Разделив обе части этого уравнения на одинаковый во всех системах отсчета малый промежуток времени Δ t, получим: При Δ t -> 0 будем иметь: Формула (4) представляет собой выражение классического закона сложения скоростей. Классический закон сложения скоростей имеет ограниченную область применения. Он выполняется с высокой степенью точности при значениях скоростей v0 и v', много меньших скорости света с в вакууме, равной 300 000 км/с. Автомобили и поезда, самолеты и космические ракеты, планеты и искусственные спутники Земли движутся относительно Земли со скоростями, значительно меньшими скорости света. Поэтому для описания их движения при переходе из системы отсчета, связанной с Землей, к любой другой системе отсчета, движущейся относительно Земли со скоростью v<<c, можно пользоваться классическим законом сложения скоростей. Особого обсуждения требует вопрос об ускорении в различных системах отсчета. Если рассматривать любые системы отсчета, движущиеся с ускорением друг относительно друга, то ускорение тела не является инвариантной величиной. Однако в системах отсчета, движущихся равномерно и прямолинейно относительно друг друга, ускорение тела одно и то же, т. е. инвариантно. К этому выводу легко прийти, используя классический закон сложения скоростей. Пусть в одной системе отсчета за промежуток времени Δ t = t1 - t2 скорость движения тела изменилась от v’1 до v’2 Скорости v’1 и v’2 в моменты времени t1 и t2 в другой системе отсчета, движущейся со скоростью v0 = const относительно первой, можно найти по закону сложения скоростей: Вычтем одно равенство из другого. Изменения скорости в обеих системах отсчета оказываются одинаковыми: Разделив обе части равенства па промежуток времени < Δ t, в течение которого произошло изменение скорости движения тела на Δ v, получим: В пределе, при Δ t - > 0, будем иметь a = a’, т. е. ускорение тела одно и то же в обеих системах отсчета. Принцип относительности Галилея. Г. Галилей, исходя из наблюдений над природными явлениями, сформулировал фундаментальный физический принцип (впоследствии названный классическим принципом относительности), согласно которому во всех инерциальных системах отсчета все механические явления протекают одинаково при одинаковых начальных условиях. Оговорка о том, что должны быть заданы одинаковые начальные условия, играет весьма существенную роль. Так, например, наблюдатели на Земле и в вагоне, движущемся относительно ее поверхности равномерно и прямолинейно, следя за свободным падением тела, увидят разныe траектории движения. Если тело в начальный момент неподвижно относительно Земли, то в системе отсчета, связанной с Землей, траекторией тела является прямая линия, а в системе отсчета, связанной с вагоном,— парабола. Это, однако, не противоречит принципу относительности, так как в этих системах отсчета различны начальные условия. В момент начала падения в системе отсчета, связанной с Землей, рассматриваемое тело покоится, а в системе отсчета, связанной с движущимся вагоном, оно имеет начальную скорость, равную по модулю скорости движения вагона относительно Земли, но направленную в противоположную сторону. Именно поэтому падение тела и выглядит неодинаково для разных наблюдателей. Но если в равномерно и прямолинейно движущемся вагоне тело в начальный момент времени неподвижно относительно вагона, то, как утверждает классический принцип относительности, в вагоне все произойдет точно так же, как и на Земле: траекторией падающего тела будет прямая. Время падения его на пол нагона будет равно времени падения тела с той же высоты на Землю. Опыты подтверждают этот принцип. Классический принцип относительности утверждает одинаковость протекания механических явлений в разных инерциальных системах отсчета, но отсюда не следует, что все механические величины в этих системах одинаковы. Например, скорость летящей птицы, измеренная в системе отсчета «берег», будет отличаться от скорости, измеренной в системе отсчета «корабль». Но нет никаких оснований считать, что одна из этих скоростей «истинная», а другая— нет. Другими словами, классический принцип относительности, раскрывая относительность некоторых характеристик движения (перемещения, координаты, скорости), утверждает абсолютность законов динамики (законов Ньютона) Именно поэтому, находясь в какой-либо инерциальной системе отсчета, нельзя с помощью механических опытов установить, движется эта система равномерно и прямолинейно или покоится. Нет никаких оснований отдать какой-либо из систем отсчета предпочтение. Специальная теория относительности (СТО). Абсолютна или относительна скорость света? Одинакова ли она во всех инерциальных системах отсчета или различна? Зависит ли скорость света от скорости движения источника или от скорости движения наблюдателя (измерительной аппаратуры)? Концепция классической механики о движении не допускает возможности абсолютной скорости у материальных объектов. Так, по классическому закону сложения скоростей Где v' и v — скорости частицы соответственно в инерциальных системах отсчета К' и K; V— скорость одной из систем отсчета относительно другой . По этому закону равенство v = v’, т.е. одинаковость скорости частицы в разных системах отсчета, исключается/так как V — конечная величина, не равная нулю. Формально v = v’ было бы возможно, если бы это были бесконечно большие величины, но скорость света конечна, и это экспериментальный факт. Если бы скорость света была относительна и подчинялась классическому закону сложения скоростей, то существовал бы в вакууме свет медленный и быстрый — свет от источников, по-разному движущихся в данной системе отсчета. Но экспериментально известно, что свет распространяется в вакууме только с одной скоростью, каковы бы ни были его источники — земные или космические, движущиеся или находящиеся в покое относительно лаборатории (измерительного прибора). Таким образом, следует признать тверди установленным экспериментальным научным фактом конечность и абсолютность (инвариантность) скорости света в вакууме Но как теоретически объяснить этот факт и понять его? На основе представлений классической механики и ee концепции о пространстве, времени и движении сделать это невозможно. Постулаты специальной теории относительности. Новая, в сравнении с классической, теоретическая концепция пространства, времени и движения была разработана А. Эйнштейном (1905 г.) и названа им специальной (частной) теорией относительности (СТО), Значительный вклад в становление и развитие идей СТО внесли X. Лоренц, А. Пуанкаре, Г. Минковский. Основу ее составляет ряд понятий и постулатов. В качестве фундаментальных традиционно выделяются два ее постулата: принцип относительности и постулат абсолютной скорости. В специальной теории относительности принцип относительности гласит: все инерциальные системы отсчета (ИСО) физически равноправны — любые физические процессы протекают в них одинаково (при одних и тех же начальных условиях). Из определения инерциальной системы отсчета и принципа относительности следует, что любая система отсчета, которая движется относительно инерциальной системы отсчета равномерно и прямолинейно, также является инерциальной. Инерциальные системы отсчета ничем не отличаются друг от друга, они полностью физически тождественны. Любую из них, в частности, можно принять за неподвижную, тогда другие будут двигаться относительно нее с различными постоянными по модулю и направлению скоростями. Постулат абсолютной скорости утверждает: совокупность всех инерциальных систем отсчета характеризуется абсолютной, конечной и постоянной величиной с размерностью скорости, обозначаемой символом с. Термин «абсолютность» употребляется здесь как синоним научного термина «инвариантность», означающего неизменность величины при каких-либо преобразованиях. В нашем случае — неизменность при переходах от одной инерциальной системы отсчета к любой другой инерциальной системе отсчета. Назовем величину с релятивистской(движущейся со скоростью света) постоянной. Экспериментальным обоснованием постулата об абсолютной скорости служат опытные факты, касающиеся свойств скорости света в вакууме. Независимость скорости света от скорости его источника подтверждается наблюдениями за двойными звездами, а также прямыми измерениями. Приведем лишь два примера. В. де Ситтер в 1913 г. наблюдал движение двойных звезд. Здесь две звезды вращаются вокруг общего центра масс, в момент излучения света вектор скорости одной из них направлен к наблюдателю, а другой — в противоположную сторону. Если бы скорость света зависела от скорости звезд, то из-за значительной удаленности двойной звезды от Земли различие в скорости распространения света от каждой звезды привело бы к оптическим искажениям истинной картины движения этих звезд в поле зрения телескопа, чего де Ситтер не обнаружил. А. М. Бонч-Бруевич в 1955 г. измерял скорости двух световых волн, идущих соответственно от диаметрально противоположных точек края солнечного диска. Из-за вращения Солнца вокруг своей оси эти точки имеют линейную скорость около 2 км/с; одна из них удаляется от наблюдателя, другая — приближается к нему. В пределах достаточно высокой точности измерений разницы в скоростях обеих световых волн не оказалось. |
|
 Типичным примером относительной величины в механике служит перемещение s тела. Если в движущемся поезде пассажир перейдет из одного конца вагона в другой, его перемещение s' (модуль) в системе отсчета, связанной с вагоном, будет равно нескольким метрам. В системе отсчета, связанной с Землей перемещение того же пассажира s (измеряемое сотнями метров) будет складываться из его перемещения относительно вагона и перемещения самого вагона относительно Земли s0:
Типичным примером относительной величины в механике служит перемещение s тела. Если в движущемся поезде пассажир перейдет из одного конца вагона в другой, его перемещение s' (модуль) в системе отсчета, связанной с вагоном, будет равно нескольким метрам. В системе отсчета, связанной с Землей перемещение того же пассажира s (измеряемое сотнями метров) будет складываться из его перемещения относительно вагона и перемещения самого вагона относительно Земли s0:  (1)
(1) (2)
(2) (3)
(3) (4)
(4)
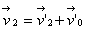
 или
или 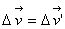
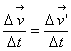
 .
.