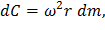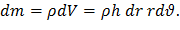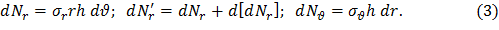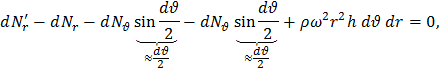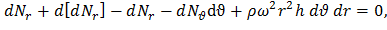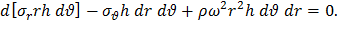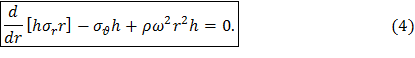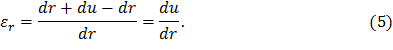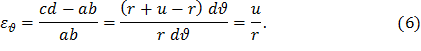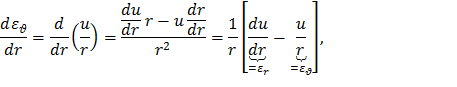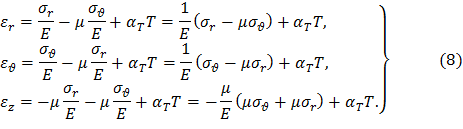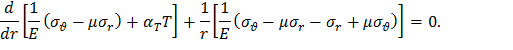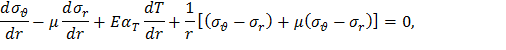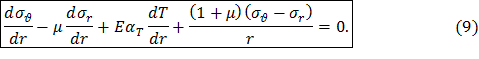|
|
Расчет напряжений и деформаций в тонком вращающемся неравномерно нагретом диске.Допущения: 1. Диск достаточно тонкий, следовательно, распределение напряжений по толщине можно принять равномерным. 2. Напряженное состояние двухосное, характеризуется радиальным напряжением σr и окружным напряжением σθ. 3. Температурное поле диска – плоское осесимметричное, то есть температура диска зависит только от радиуса Т(r) и постоянна по толщине. 4. Свойства материала (модуль упругости E и коэффициент Пуассона μ) – постоянные для всего диска, их зависимостью от температуры пренебрегаем. Пусть диск вращается с угловой скоростью ω. Рассмотрим сектор симметрии диска, приходящийся на одну рабочую лопатку. Введем следующие обозначения (рис.7): – радиус внешней цилиндрической поверхности или периферийный радиус - r1;
– радиус внутренней цилиндрической поверхности (радиус расточки диска) – r0; – толщина диска на окружности радиуса r1 (на периферии) - h1; – толщина диска на окружности радиуса r0 (на расточке) - h0. – на внешней цилиндрической поверхности при r=r1 действуют равномерно распределенные по толщине напряжения σr1, обусловленные центробежными силами обода и рабочих лопаток,
где t1 – шаг лопаток по окружности радиуса r1; С – центробежная сила одной лопатки; Соб – центробежная сила обода диска, отнесенная к шагу t1; – на внутренней цилиндрической поверхности при r=r0 действуют равномерно распределенные по толщине напряжения σr0, обусловленные контактным давлением посадки диска на вал q0. Необходимо определить распределение радиальных и окружных напряжений по радиусу диска – σr(r) и σθ(r). Для решения поставленной задачи следует составить уравнения равновесия и совместности деформаций, а также выбрать закон деформирования. Рассмотрим элемент диска, выделенный из сектора симметрии (рис. 7) двумя цилиндрическими сечениями на радиусах r и r+dr и двумя меридиональными плоскостями с углом dθ между ними (рис. 8).
где dm – масса выделенного элемента, составляющая
Таким образом, центробежная сила инерции выразится как
где ρ – плотность материала диска. Согласно методу сечений со стороны отброшенной части тела на поверхностях, ограничивающих выделенный элемент, будут действовать поверхностные силы
Составим уравнение равновесия, спроецировав силы (2) и (3) на направление радиуса,
Продифференцировав последнее выражение последовательно по dθ и dr, получаем
Уравнение равновесия (4) содержит две неизвестных (σr и σθ), следовательно, задача статически неопределима. Для получения второго уравнения рассмотрим деформации выделенного элемента диска. Деформация диска будет заключаться в его удлинении в радиальном направлении. Радиальное перемещение точек внутренней поверхности – u. Точки наружной поверхности переместятся по радиусу на u+du. Следовательно, толщина выделенного элемента dr увеличится на du (рис. 8). Таким образом, относительные линейные деформации в радиальном направлении составят
В окружном направлении относительные линейные деформации εθ будут равны относительному удлинению дуги ab=rdθ, занявшей положение cd=(r+u)dθ (рис. 8)
Продифференцировав выражение (6) по радиусу r
окончательно получим уравнение совместности деформаций
Уравнения равновесия (4) и совместности деформаций (7) не зависят от закона деформирования и одинаково применимы как к упругому диску, так и в условиях упругопластических деформаций или ползучести. Рассмотрим диск в условиях упругости. Уравнения, связывающие напряжения и деформации, выражены законом Гука в следующем виде
Подставив формулы (8) в уравнение совместности деформаций (7), получим
Умножим полученное выражение на E и окончательно получим
Система уравнений (4) и (9) содержит две неизвестные величины σr и σθ. Её решение позволит определить искомые напряжения, которые должны удовлетворять граничным условиям:
где q0 – давление посадки диска на валу. В общем случае, когда диск имеет переменную толщину h(r), для решения полученной системы уравнений необходимо применение численных методов. Рассмотрим частный случай диска постоянной толщины, для которого существует простое аналитическое решение. |
|

 – поправочный коэффициент (0,7 – 1);
– поправочный коэффициент (0,7 – 1);