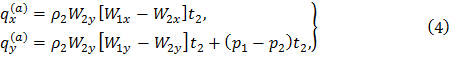Рабочие лопатки последних ступеней ЧНД. Рабочие лопатки имеют значительную длину и dc/l=2…3 (рис. 11). Профильная часть представляет собой закрученный стержень переменного поперечного сечения, исполненный заодно с хвостовиком и бандажом. Хвостовик лопатки может быть вильчатого или елочного типа с криволинейной осью, выполненной по дуге окружности.
При установке лопаток на диск периферийные бандажи входят в зацепление по поверхности контакта. Под действием центробежных сил периферийное сечение лопатки с бандажом стремится повернуться. На поверхности контакта возникает давление, обеспечивающее трение при относительном смещении смежных лопаток, а, следовательно, и демпфирование при колебаниях.
 | Рис. 11. Рабочая лопатка последней ступени ЧНД
|
Через отверстия в профильной части лопатки протянута проволока, замкнутая на круг. Для снижения концентрации напряжения около отверстий предусмотрено утолщение.
Напряжения и деформации рабочих лопаток в условиях упругости
Координатные оси рабочих лопаток
Рассмотрим одну изолированную рабочую лопатку турбомашины, закрепленную на диске (рис. 12). Начало координат расположено в геометрическом центре корневого сечения лопатки. Ось z направлена по радиусу от оси вращения диска, ось х – по направлению окружной скорости центра корневого сечения, ось y – параллельно оси диска в сторону вектора угловой скорости.
Для поперечного сечения лопатки плоскостью S, перпендикулярной оси z, начало координат расположено в геометрическом центре сечения.
| Рис. 12. Координатные оси лопатки (а) и профиля (б)
|
Оси ξ и η – главные центральные оси сечения, βу – установочный угол. Главная ось η проходит примерно параллельно хорде профиля. Тогда угол между осями ξ и х составит β≈900– βу.
Приведенное на рисунке расположение лопатки и профиля соответствует случаю, когда осевое движение рабочего тела совпадает по направлению с вектором угловой скорости.
Усилия, действующие на рабочую лопатку
Рабочие лопатки испытывают воздействия от центробежных сил вращения, аэродинамических сил потока пара или газа, а также температурные воздействия.
Центробежные силы относятся к стационарным или медленноизменяющимся воздействиям. Следовательно, от них зависит статическая кратковременная и длительная прочность лопаток. Эти силы вызывают статическое растяжение, изгиб и кручение рабочих лопаток.
Аэродинамические силы имеют стационарную и переменную составляющие. Первые вызывают статический изгиб и кручение, и влияют на статическую прочность. Вторые вызывают колебания и определяют вибрационную надежность лопаточного аппарата.
При переходных режимах, таких как пуск, нагружение, разгрузка, останов, из-за неравномерного прогрева и охлаждения в рабочих лопатках возникают температурные напряжения. При повторении таких режимов температурные воздействия определяют термоциклическую прочность рабочих лопаток.
Уравнения равновесия лопатки
Для определения внутренних силовых факторов рассмотрим равновесие элемента лопатки под действием аэродинамических сил и центробежных сил инерции. Рассмотрим элемент лопатки, выделенный двумя сечениями на расстоянии z и z+dz от начала координат. Ось лопатки в деформированном состоянии и схема нагружения выделенного элемента показана на рис. 13. Здесь u и v – смещения (прогибы) в сечении соответственно в направлении осей x и y; θу – угол наклона оси лопатки.
На поперечных сечениях элемента действуют растягивающие силы N и N1, перерезывающие силы Qx и Qx1 и изгибающие моменты My и My1. На выделенный элемент так же действуют распределенные (объемные) центробежные силы инерции и поверхностные аэродинамические силы.
Центробежные силы.
Элементарная центробежная сила, действующая на выделенный элемент dz, определяется как

где ν=ρF – линейная плотность (масса, приходящаяся на единицу длины лопатки). Проекции этой силы на оси z, x и y составят соответственно

| Рис. 13. Лопатка в деформированном состоянии
а – проекция на плоскость xOz;
б – проекция на плоскость yOz;
в – схема нагружения элемента лопатки в плоскости xOz.
|
Проекция центробежной силы на ось y равна нулю, поскольку она может действовать только в плоскости вращения.
Тогда нагрузка на единицу длины лопатки от центробежных сил инерции вдоль оси x составит

Аэродинамические силы.
Аэродинамическая нагрузка, приходящаяся на единицу длины оси лопатки, известна из теплового расчета турбины и определяется соотношениями
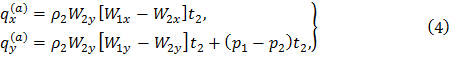
q(a)x, q(a)y – аэродинамические нагрузки по осям x и y; ρ2 – плотность среды за рабочими лопатками; W1x, W1y – проекции относительной скорости перед рабочими лопатками соответственно на оси x и y (осевая и окружная составляющие); W2x, W2y – проекции относительной скорости за рабочими лопатками соответственно на оси x и y (осевая и окружная составляющие); t2 – шаг рабочих лопаток; p1 и p2 – статическое давление соответственно перед и за рабочими лопатками.
Кроме перечисленных нагрузок на лопатку действует аэродинамический крутящий момент, определение которого требует расчета распределения давления по контуру профиля. Аэродинамический крутящий момент оказывает незначительное влияние на напряжения и деформации рабочих лопаток.
|