|
|
Уравнение Ван - дер - Ваальса. График уравнения Ван - дер - Ваальса.Наиболее содержательные результаты получаются из уравнения Ван-дер-Ваальса путем анализа его изотерм. Для одного моля газа (n = 1) уравнение изотермы можно представить в виде При высоких температурах последний член в (5) можно опустить, и тогда изотерма будет гиперболой, асимптотами которой являются изобара Р = 0 и изохора V = b . Для исследования изотерм при любых значениях Т умножим уравнение (4) на V2. После раскрытия скобок уравнение изотермы примет вид Это уравнение третьей степени по V , в которое давление Р входит в качестве параметра. Поскольку его коэффициенты вещественны, уравнение имеет либо один вещественный корень, либо три корня. Каждому корню на плоскости (V,P) соответствует точка, в которой изобара Р = const пересекает изотерму. В первом случае, когда корень один и точка пересечения будет одна. Так будет, как мы видели, при любых давлениях, если температура достаточно высока. Изотерма имеет вид монотонно опускающейся кривой MN.
Для нахождения критических параметров Pk, Vk, Tk учтем, что в критической точке уравнение (6) переходит в уравнение Поскольку в этом случае все три корня совпадают и равны Vk , уравнение должно приводиться к виду Возводя в куб и сравнивая коэффициенты уравнений (7) и (8), получим три уравнения Решая их, найдем выражения для параметров критического состояния вещества: К тем же результатам можно прийти, заметив, что критическая точка К является точкой перегиба изотермы, касательная в которой горизонтальна, а поэтому в точке К должны соблюдаться соотношения Решая эти уравнения совместно с уравнением изотермы (4) придем к формулам (9). Не все состояния вещества, совместимые с уравнением Ван-дер-Ваальса, могут быть реализованы в действительности. Для этого необходимо еще, чтобы они были термодинамически устойчивы. Одно из необходимых условий термодинамической устойчивости физически однородного вещества состоит в выполнении неравенства Таким образом, реальная изотерма распадается на две ветви EGA и BLD , отделенные друг от друга. Естественно предположить, что этим двум ветвям соответствуют различные агрегатные состояния вещества. Ветвь EA характеризуется относительно большими значениями объема или малыми значениями плотности, она соответствует газообразному состоянию вещества. Напротив, ветвь BD характеризуется относительно малыми объемами, а следовательно, большими плотностями, она соответствует жидкому состоянию вещества. Мы распространяем, следовательно, уравнение Ван-дер-Ваальса и на область жидкого состояния. Таким путем удается получить удовлетворительное качественное описание явления перехода газа в жидкость и обратно. Возьмем достаточно разреженный газ при температуре ниже критической. Исходное состояние его на диаграмме PV изображается точкой E (рис. 1). Будем сжимать газ квазистатически, поддерживая температуру T постоянной. Тогда точка, изображающая состояние газа, будет перемещаться по изотерме вверх. Можно было думать, что она достигает крайнего положения A , где изотерма обрывается. В действительности, однако, начиная с некоторой точки G , давление в системе перестает повышаться, и она распадается на две физически однородные части, или фазы: газообразную и жидкую. Процесс изотермического сжатия такой двухфазной системы изображается участком GL горизонтальной прямой. При этом во время сжатия плотности жидкости и газа остаются неизменными и равными их значениям в точках L и G соответственно. По мере сжатия количество вещества в газообразной фазе непрерывно уменьшается, а в жидкой фазе - увеличивается, пока не будет достигнута точка L, в которой все вещество перейдет в жидкое состояние. Эндрюс систематически исследовал ход изотерм углекислоты (СО2) при различных температурах и на основе этих исследований ввел понятие критической температуры. Углекислота им была выбрана сознательно, так как она обладает критической температурой (310 С), лишь незначительно превышающей комнатную, и сравнительно невысоким критическим давлением (72,9 атм). Оказалось, что при температуре выше 310 С изотермы углекислоты монотонно опускаются вниз, т.е. имеют гиперболический вид. Ниже этой температуры на изотермах углекислоты появляются горизонтальные участки, на которых изотермическое сжатие газа приводит к его конденсации, но не к увеличению давления. Таким путем было установлено, что сжатием газ можно превратить в жидкость только тогда, когда его температура ниже критической. При специальных условиях могут быть реализованы состояния, изображаемые участками изотермы GA и BL. Эти состояния называются метастабильными. Участок GA изображает так называемый пересыщенный пар, участок BL - перегретую жидкость. Обе фазы обладают ограниченной устойчивостью. Каждая из них может существовать до тех пор, пока она не граничит с другой более устойчивой фазой. Например, пересыщенный пар переходит в насыщенный, если в него ввести капли жидкости. Перегретая жидкость закипает, если в нее попадают пузырьки воздуха или пара.
|
|
 , (4). если считать температуру Т постоянной. Перепишем уравнение (4) в виде
, (4). если считать температуру Т постоянной. Перепишем уравнение (4) в виде  (5).
(5).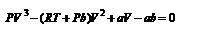 (6)
(6)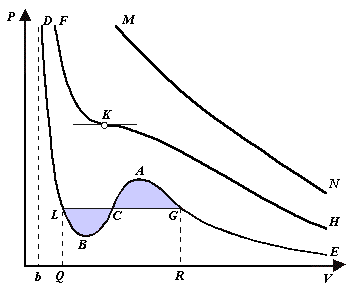 При более низких температурах и надлежащих значениях давления Р уравнение (6) имеет три корня V1, V2, V3 . В таких случаях изобара P = const пересекает изотерму в трех точках L, C, G (рис. 1). Изотерма содержит волнообразный участок LBCAG. Она сначала монотонно опускается вниз (участок DB), затем на участке BA монотонно поднимается вверх, а за точкой A снова монотонно опускается. При некоторой промежуточной температуре три корня V1, V2, V3 становятся равными. Такая температура и соответствующая ей изотерма называются критическими. Критическая изотерма FKH всюду монотонно опускается вниз, за исключением одной точки K, являющейся точкой перегиба изотермы. В ней касательная к изотерме горизонтальна. Точка K называется критической точкой. Соответствующие ей давление Pk , объем Vk и температура Tk называются также критическими. Говорят, что вещество находится в критическом состоянии, если его объем и давление (а следовательно, и температура) равны критическим.
При более низких температурах и надлежащих значениях давления Р уравнение (6) имеет три корня V1, V2, V3 . В таких случаях изобара P = const пересекает изотерму в трех точках L, C, G (рис. 1). Изотерма содержит волнообразный участок LBCAG. Она сначала монотонно опускается вниз (участок DB), затем на участке BA монотонно поднимается вверх, а за точкой A снова монотонно опускается. При некоторой промежуточной температуре три корня V1, V2, V3 становятся равными. Такая температура и соответствующая ей изотерма называются критическими. Критическая изотерма FKH всюду монотонно опускается вниз, за исключением одной точки K, являющейся точкой перегиба изотермы. В ней касательная к изотерме горизонтальна. Точка K называется критической точкой. Соответствующие ей давление Pk , объем Vk и температура Tk называются также критическими. Говорят, что вещество находится в критическом состоянии, если его объем и давление (а следовательно, и температура) равны критическим. (7).
(7). (8).
(8). .
. (9).
(9). .
. . Физически оно означает, что при изотермическом увеличении давления объем тела должен уменьшаться. Иными словами, при возрастании V все изотермы должны монотонно опускаться. Между тем, ниже критической температуры на изотермах Ван-дер-Ваальса имеются поднимающиеся участки типа BCA (рис. 1). Точки, лежащие на таких участках, соответствуют неустойчивым состояниям вещества, которые практически реализованы быть не могут. При переходе к практическим изотермам эти участки должны быть выброшены.
. Физически оно означает, что при изотермическом увеличении давления объем тела должен уменьшаться. Иными словами, при возрастании V все изотермы должны монотонно опускаться. Между тем, ниже критической температуры на изотермах Ван-дер-Ваальса имеются поднимающиеся участки типа BCA (рис. 1). Точки, лежащие на таких участках, соответствуют неустойчивым состояниям вещества, которые практически реализованы быть не могут. При переходе к практическим изотермам эти участки должны быть выброшены.