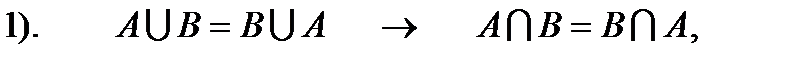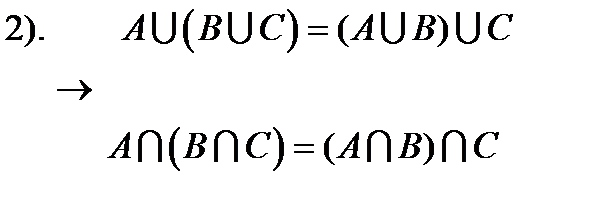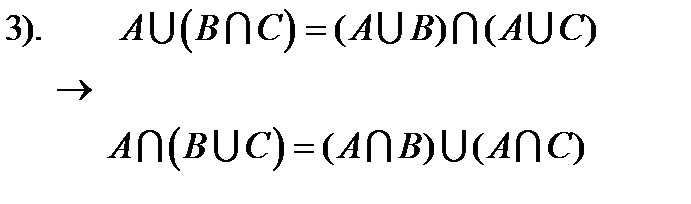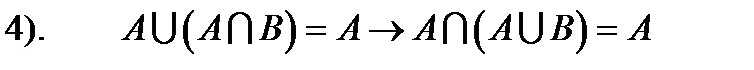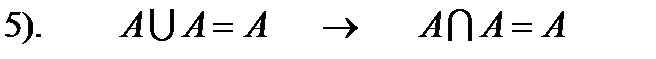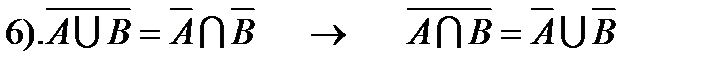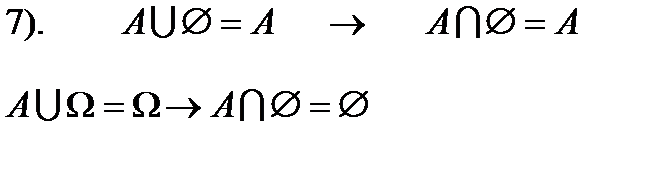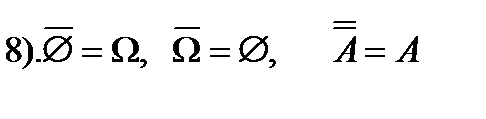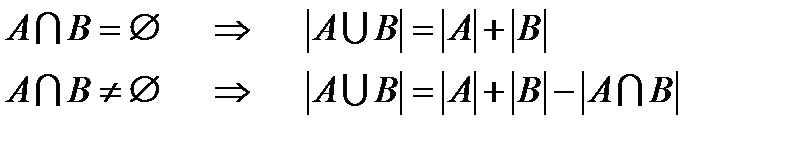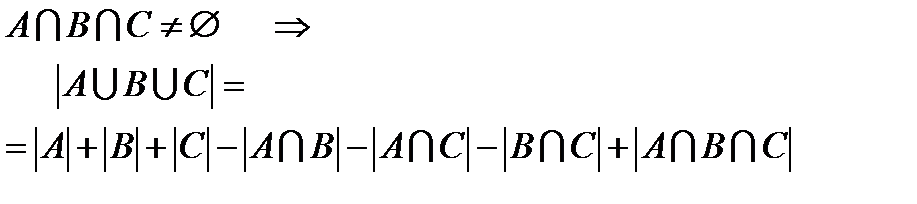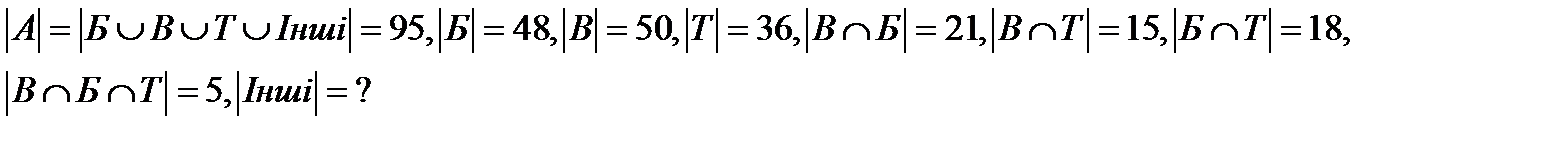|
|
Розглянемо операції над множинами, які є підмножинамит універсальної.Задання і запис множин Довільна множина задається переліком елементів у фігурних дужках: A = {a, b, c, d}. Множини натуральних, цілих, раціональних, дійсних, простих чисел: N = {1, 2, 3, … , n, …}, Перелічити всі елементи множини не завжди можливо, тому у загальному випадку довільну множину вважають заданою, якщо існує деяка умова. Приклад: B = {–3, –2, –1, 0, 1, 2, 3} = { x | Множина, яка не має жодного елемента називається порожньою
Множина А - підмножина множини В: Множина А являється підмножиною множини В, якщо кожний елемент множини А належить множині В:
Джордж Буль (англ. George Boole), (1815—1864) — британський математик і філософ. У 1854 р. побачив світ основний твір Буля «Дослідження законів думки, на яких засновані математичні теорії логіки й імовірності». Ця ґрунтовна книга нині зараховується до математичної класики; у ній детально досліджується та система алгебри, яку сьогодні називають «алгеброю висловлювань». У своїх працях «Логічне мислення» (1842), «Математичний аналіз логіки» (1847), «Дослідження законів мислення»(1854) заклав основи математичної логіки. Дж. Буль вперше розглянув алгебри, подібні до алгебри множин, остання є одним з прикладів бульової алгебри. До речі, чотири дочки Буля здобули популярність як вчені (геометр Алісія, хімік Люсі), або члени вчених сімей (Мері, дружина математика й письменника Ч. Г. Хінтона, і Маргарет, мати математика Дж. І. Тейлора), а п'ята - Етель Ліліан Войнич - прославилася як письменниця - є авторкою видатного романа «Овод». Матеріальне становище його батьків було дуже скрутним; тому, не зважаючи на виражений потяг молодого Джорджа до знань, батьки не змогли дати йому систематичної освіти і, окрім початкових класів школи для дітей бідняків, Буль не вчився в жодному навчальному закладі. Втім, можливо, частково цією обставиною пояснюється вражаюча оригінальність Буля і свіжість його думки, яка ніколи не шукала второваних шляхів: адже він не відчував тиску традицій, втілених у налагодженій системі масової освіти. Нешаблонність наукової творчості Буля затримала дійсне визнання заслуг Буля, яке прийшло лише тоді, коли самого Буля вже давно не було в живих. Булева алгебра має тісні зв’язки з багатьма важливими напрямками математичної науки. Загальнотеоретичне і прикладне значення булевої алгебри визначають тією існуючою роллю, яку вона відіграє в математичній логіці, теорії ймовірності і кібернетиці. В( А ) - Булеан множини А - множина всіх підмножин множини А 1).
2).
3).
Взагалі доведено:
Універсальна множина: Діаграми Ейлера-Венна Leonard Euler(1707—1873), John Venn,( 1834—1923):
Ейлер увічнений в шостій серії швейцарських 10 франків і на численних швейцарських, німецьких та російських поштових марках. На його честь названо астероїд 2002 Ейлер. Він також відзначений лютеранською церквою у церковному календарі (24 травня) — Ейлер був побожним християнином, вірив в біблійну непогрішність, рішуче виступав проти видатних атеїстів свого часу.
Цікаво, що у їдальні Кембриджа в його пам'ять встановлений вітраж із зображенням діаграми Венна. В університеті міста Халл в 1928 на його честь було споруджено будинок. В ході недавнього опитування BBC, Венн був визнаний третім найвеличнішим математиком сучасності після сера Ісаака Ньютона і Леонарда Ейлера. При вирішенні цілого ряду завдань Леонард Ейлер використовував ідею зображення множин за допомогою кіл. Особливого розквіту графічні методи досягли в творах англійського логіка Джона Венна, який докладно виклав їх у книзі «Символічна логіка», виданій в Лондоні в 1881 році. Тому такі схеми іноді називають Діаграми Ейлера — Венна. Діаграма Венна зображує, всі можливі перетини множин. Всього таких перетинів буде
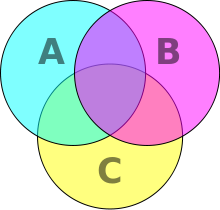
Діаграма Ейлера-Венна для множин A, B, та C
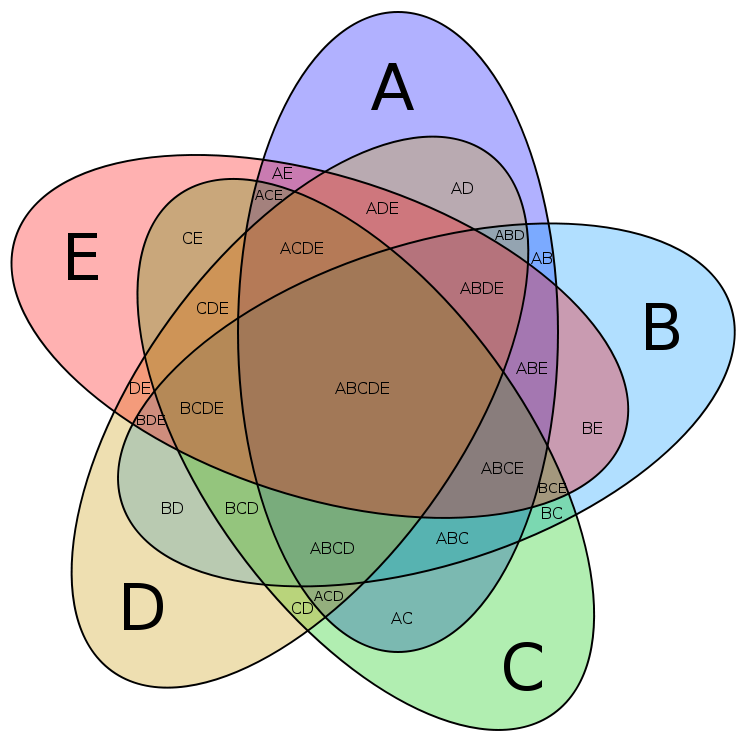
Діаграма Ейлера- Венна для 5 множин утворена еліпсами, створена Бранко Грюнбаумом. Кожна частина підписана. РІВНІСТЬ МНОЖИН:
1. А=А – рефлексивність 2. 3. ОПЕРАЦІЇ НАД МНОЖИНАМИ: Розглянемо операції над множинами, які є підмножинамит універсальної. 1. Додавання множин:
2. Множення множин:
3. Віднімання множин: А В
4. Доповнення множин:
5. Теорема де Моргана: (Augustus de Morgan, 1806— 1871)
6. Принцип двоїстості алгебри множин:
Правило сумми
Приклади
КОМБІНАТОРИКА Комбінато́рика (Комбінаторний аналіз) — розділ математики, присвячений розв'язанню задач вибору та розташування елементів деякої, зазвичай, скінченної множини відповідно до заданих правил. Кожне таке правило визначає спосіб побудови деякої конструкції із елементів вихідної множини, що зветься комбінаторною конфігурацією. Тому на меті комбінаторного аналізу стоїть дослідження комбінаторних конфігурацій, алгоритмів їх побудови, оптимізація таких алгоритмів, а також розв'язання задач переліку. З комбінаторикою мають справу хіміки при вивченні різних можливих типів зв'язків атомів у молекулах; біологи, наприклад, у процесі знаходження послідовностей амінокислот у білкових сполуках; кібернетики при розв'язанні задач кодування й побудові обчислювальних пристроїв, математики — при розв'язанні багатьох різних задач, особливо в теорії ймовірності. Також комбінаторику використовують у своїх моделях фізики, архітектори, економісти й представники багатьох інших наук. Найпростішими прикладами комбінаторних конфігурацій є перестановки, розміщення, сполучення. Термін «комбінаторика» ввів Лейбніц, який у 1666 році опублікував свою працю «Міркування про комбінаторне мистецтво». |
|
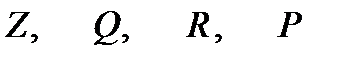 .
. ‚ | x | <4};
‚ | x | <4}; 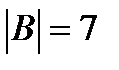
 одноелементна множина:
одноелементна множина: 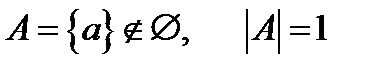
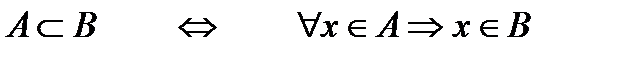
 - невласні підмножини множини А, всі інші підмножини – власні
- невласні підмножини множини А, всі інші підмножини – власні
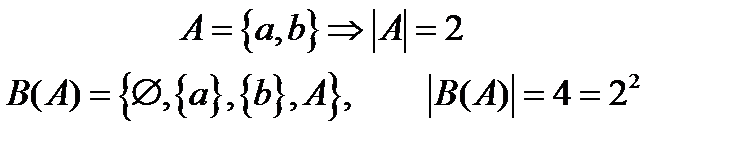
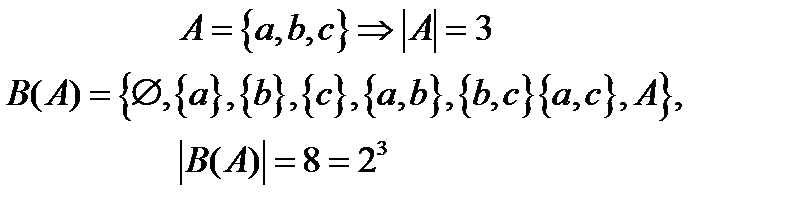


 - множина,різні підмножини якої доводиться розглядати .
- множина,різні підмножини якої доводиться розглядати . Леона́рд Е́йлер (1707—1783) — швейцарський математик та фізик, який провів більшу частину свого життя в Росії та Німеччині. Ейлер здійснив важливі відкриття в таких різних галузях математики, як математичний аналіз та теорія графів. Він також ввів велику частину сучасної математичної термінології і позначень, зокрема у математичному аналізі, як, наприклад, поняття математичної функції. Ейлер відомий також завдяки своїм роботам в механіці, динаміці рідини, оптиці та астрономії, інших прикладних науках. Ейлер вважається найвидатнішим математиком 18-го століття, а, можливо, навіть усіх часів. Він також є одним із найплідніших — збірка всіх його творів зайняла б 60-80 томів. Вплив Ейлера на математику описує висловлювання «Читайте Ейлера, читайте Ейлера, він є метром усіх нас», яке приписується Лапласові (фр. Lisez Euler, lisez Euler, c'est notre maître à tous).
Леона́рд Е́йлер (1707—1783) — швейцарський математик та фізик, який провів більшу частину свого життя в Росії та Німеччині. Ейлер здійснив важливі відкриття в таких різних галузях математики, як математичний аналіз та теорія графів. Він також ввів велику частину сучасної математичної термінології і позначень, зокрема у математичному аналізі, як, наприклад, поняття математичної функції. Ейлер відомий також завдяки своїм роботам в механіці, динаміці рідини, оптиці та астрономії, інших прикладних науках. Ейлер вважається найвидатнішим математиком 18-го століття, а, можливо, навіть усіх часів. Він також є одним із найплідніших — збірка всіх його творів зайняла б 60-80 томів. Вплив Ейлера на математику описує висловлювання «Читайте Ейлера, читайте Ейлера, він є метром усіх нас», яке приписується Лапласові (фр. Lisez Euler, lisez Euler, c'est notre maître à tous). Джон Венн (1834—1923) — англійський логік и філософ. Він відомий тим, що запровадив діаграми Венна, які використовуються в багатьох областях, таких як теорія множин, теорія ймовірностей, логіка, статистика й інформатика.
Джон Венн (1834—1923) — англійський логік и філософ. Він відомий тим, що запровадив діаграми Венна, які використовуються в багатьох областях, таких як теорія множин, теорія ймовірностей, логіка, статистика й інформатика.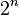 , де n — кількість множин.
, де n — кількість множин.
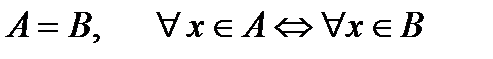
 - симетричність
- симетричність - транзитивність
- транзитивність ,
, 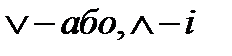



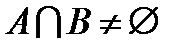
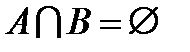
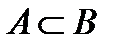
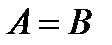
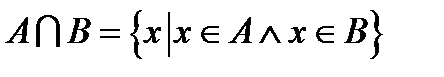
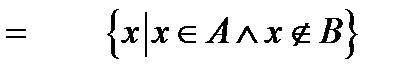

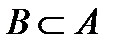
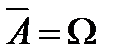

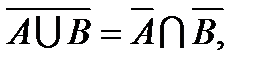
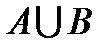




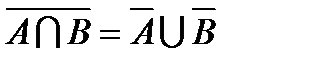 (самостійно довести графічно)
(самостійно довести графічно)