|
|
ОЦЕНКА ПОГРЕШНОСТЕЙ РАВНОТОЧНЫХ ИЗМЕРЕНИЙ
Одной из важнейших задач измерения является умение оценить меру приближения результата наблюдения к действительному значению измеренной величины. Эта задача сводится к нахождению оценок параметров функции распределения случайной величины на основании выборки — ряда значений, принимаемых этой величиной в п независимых опытах. Выше указывалось, что наиболее вероятным значением искомой величины является среднее арифметическое наблюденных значений. Из этого, однако, не следует, что среднее арифметическое ближе к действительному значению, чем результат каждого отдельного наблюдения. Напротив, некоторые из результатов наблюдений могут быть ближе к Q, но, к сожалению, мы не можем выбрать эти результаты из числа других результатов ряда. Именно поэтому приходится определять среднее арифметическое. При каждом наблюдении величины А мы будем получать наблюдения х1, х2, ..., отклонения которых от действительного значения будут различны. Чем больше наблюдений будет выполнено, тем меньше влияние отклонения отдельного наблюдения па отклонение среднего арифметического от действительного значения измеренной величины. При определении погрешностей наблюдение будем рассматривать равноточные измерения. Равноточными измерениями называются такие, которые про водятся при одних и тех же условиях, одним и тем же исследователем, пользующимся одним и тем же прибором, а все результата являются независимыми, одинаково распределенными случайными величинами. Допустим, что наши результаты измерений свободны от систематических погрешностей (они известны и исключены из результатов измерений). Имеют место только случайные погрешности которые независимы между собой и подчиняются нормальному закону распределения. Необходимо определить, какова точность определения измеряемой величины и какова надежность ее получения. Ранее было установлено, что вследствие неизбежных погрешностей результат измерения всегда будет отличаться от действительного значения измеренной величины. Следовательно, можно предположить, что действительное значение измеряемой величины всегда находится где-то в окрестности значений X. Если на числовой оси около точки X взять интервал с границами X — ԑ; X + ԑ, то вероятность того, что действительное значение измеряемой величины 0. лежит в пределах этого интервала, будет представлять собой доверительную вероятность или коэффициент надежности
Интервал (X — ԑ; X + ԑ) называется доверительным интервалом. Равенство (2.23) означает, что с вероятностью а результат наблюдения не выходит за пределы доверительного интервала. По мере увеличения доверительного интервала (т. е. уменьшения точности) увеличивается и надежность Величина Q окажется вне интервала (X — ԑ; X + ԑ) в том случае, если погрешность измерения по абсолютной величине превысит е:
Если погрешности измерений распределены по нормальному закону, то вероятность того, что случайная величина лежит в пределах
может быть найдена по формулам (2.20), (2.22)
Пользуясь таблицей функции Лапласа, можно найти значения надежности для заданной точности и, наоборот, по заданной надежности можно найти величину доверительного интервала. Ниже приведены некоторые значения отношения е/а и соответствующие им значения надежности а, выраженные в процентах.
Следует обратить внимание на следующее. Так, при отношении Например, математическое ожидание мы заменяем средним арифметическим результатом ограниченного числа наблюдений. При большом числе опытов значение среднего арифметического весьма близко к математическому ожиданию. Если же число опытов не велико, то замена математического ожидания средним арифметическим приводит к погрешности. Иными словами, если мы измеряли величину Q и получили среднее арифметическое
где
Для оценки точности среднего результата ограниченного числа наблюдений воспользуемся теорией выборок. Пусть все возможные результаты измерений X составляют генеральную совокупность, а полученные нами значения хi — выборку из нее. Объем выборки равен числу результатов наблюдения. Величину X в генеральной совокупности будем считать распределенной нормально со средним арифметическим Полагая измерения свободными от систематических погрешностей, можем считать, что среднее генеральной совокупности Среднее из полученных нами результатов п измерений не всегда будет равно среднему генеральной совокупности Закон распределения средних значений из выборок генеральной совокупности нормального закона распределения представляет также нормальный закон со средним значением, равным среднему значению генеральной совокупности, и дисперсией, равной частному от деления дисперсии генеральной совокупности на объем выборки. Следовательно, дифференциальный закон распределения среднего значения
где В этом случае надежность результата при заданной точности будет
Числовые значения надежности можно также определить, пользуясь приложением 2. Только величины, стоящие в верхней строке, будут выражены в долях выборочной средней:
Иными словами, точность среднего результата из п измерений выше точности единичного измерения в
Найденная нами дисперсия
За приближенное значение дисперсии генеральной совокупности принимают
Оценка среднего квадратического отклонения результатов наблюдений
При большом количестве опытов п (практически при п > 20) дисперсия так же, как и в случае, когда известно вычисленное по (2.27):
Если же п не достаточно велико (
имеет дифференциальный закон распределения вероятностей, описываемый функцией
где В выражении, определяющем величину t,
При этом рассматриваемое неравенство
можно записать в виде
Вероятность того, что величина будет находиться в интервале
Это и является оценкой надежности среднего арифметического, как результата измерения, заданного неравенством
Рассмотрим примеры пользования приложением II. Пример 2. Какова величина доверительного интервала при надежности По таблице Стьюдента (см. приложение II) находим для Доверительный интервал
Следовательно, с вероятностью 0,98 можно утверждать, что
Пример 3. Необходимо определить, какова надежность того, что при условиях примера 2 доверительный интервал не будет превышать 0,02. Находим величину Пользуясь таблицей Стьюдента, можно определить, каково должно быть число измерений при заданных точности и надежности. Для этого напишем следующее равенство:
Таблица 2.1.
Необходимое число измерений для обеспечения заданной надежностиа и относительной погрешности
Величину
Результаты решения уравнения сведены в табл. 2.1, которая дает необходимое число измерений для обеспечения заданной надежности 12 |
|
 (2.23)
(2.23) , т. е. чем больший доверительный интервал мы задаем, тем вероятнее, что результаты наблюдений не выйдут за его пределы. Следовательно, для характеристики величины случайной погрешности необходимо задать два числа: величину доверительного интервала и величину доверительной вероятности. Указание только одной величины погрешности без указания соответствующей доверительной вероятности недостаточно, так как не характеризует степень надежности полученного результата измерения.
, т. е. чем больший доверительный интервал мы задаем, тем вероятнее, что результаты наблюдений не выйдут за его пределы. Следовательно, для характеристики величины случайной погрешности необходимо задать два числа: величину доверительного интервала и величину доверительной вероятности. Указание только одной величины погрешности без указания соответствующей доверительной вероятности недостаточно, так как не характеризует степень надежности полученного результата измерения. .
. ,
, . (2.24)
. (2.24)
 , практически равна нулю. Все рассмотренные числовые характеристики относятся к законам распределения случайных величин. Известно, что для выявления закона распределения необходимо располагать результатами весьма большого количества измерений. Однако на практике в большинстве случаев нам приходится пользоваться результатами ограниченного числа измерений — двадцати, десяти, а иногда и меньше. Любое значение искомого параметра закона распределения, вычисленное на основе ограниченного числа опытов, всегда будет содержать элемент случайности.
, практически равна нулю. Все рассмотренные числовые характеристики относятся к законам распределения случайных величин. Известно, что для выявления закона распределения необходимо располагать результатами весьма большого количества измерений. Однако на практике в большинстве случаев нам приходится пользоваться результатами ограниченного числа измерений — двадцати, десяти, а иногда и меньше. Любое значение искомого параметра закона распределения, вычисленное на основе ограниченного числа опытов, всегда будет содержать элемент случайности.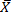 по результатам п измерений то
по результатам п измерений то ,
,
 и средним квадратическим отклонением
и средним квадратическим отклонением  .
. .
. (2.25)
(2.25) — дисперсия генеральной совокупности;
— дисперсия генеральной совокупности;  — дисперсия средней выборочной.
— дисперсия средней выборочной.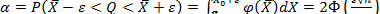 (2.26)
(2.26) (2.27)
(2.27) раз. Как видно из (2.27), для оценки надежности среднего результата необходимо знать дисперсию генеральной совокупности. Обычно дисперсия не известна до опыта и о ней приходится судить на основании результатов измерения. Однако, основываясь на результатах п измерений, можно найти лишь дисперсию этих результатов относительно своей выборочной средней
раз. Как видно из (2.27), для оценки надежности среднего результата необходимо знать дисперсию генеральной совокупности. Обычно дисперсия не известна до опыта и о ней приходится судить на основании результатов измерения. Однако, основываясь на результатах п измерений, можно найти лишь дисперсию этих результатов относительно своей выборочной средней  (2.28)
(2.28) не равна дисперсии генеральной совокупности; она несколько меньше последней. Математическое ожидание выборочной дисперсии
не равна дисперсии генеральной совокупности; она несколько меньше последней. Математическое ожидание выборочной дисперсии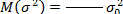
 (2.29)
(2.29) (2.30)
(2.30) осуществляется
осуществляется
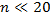 ), надежность среднего результата измерений определяется с помощью распределения Стьюдента, согласно которому величина
), надежность среднего результата измерений определяется с помощью распределения Стьюдента, согласно которому величина
 (2.31)
(2.31) называется количеством степеней свободы в распределении Стьюдента.
называется количеством степеней свободы в распределении Стьюдента. .
.
 (2.32)
(2.32) , определится выражением
, определится выражением (2.33)
(2.33) , удовлетворяющие заданной надежности
, удовлетворяющие заданной надежности (2.34)
(2.34) и
и  .
.
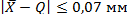
 . По таблице Стьюдента (см. приложение II) для п = 10 и t= 0,64 путем интерполяции между значениями
. По таблице Стьюдента (см. приложение II) для п = 10 и t= 0,64 путем интерполяции между значениями  (2.35)
(2.35)
 , выражающую границу доверительного интервала в долях величины дисперсии, называют также относительной погрешностью
, выражающую границу доверительного интервала в долях величины дисперсии, называют также относительной погрешностью (2.36)
(2.36)