|
|
Элементарные преобразования матриц.Элементарными преобразованиями матриц являются: 1. Перестановка двух любых строк или столбцов 2. Умножение строки или столбца на число, отличное от нуля 3. Прибавление к некоторой строке (столбцу) другую строку (столбец). 4. (Иногда к числу элментарных преобразований относят транспонирование матрицы) *При элементрарных преобразованиях ранг матрицы не меняется. Теорема о сохранении ранга матрицы при элементарных преобразованиях. Справедлива теорема о сохранении ранга матрицы.При элементарных преобразованиях матрицы ранг матрицы не меняется.
Арифметическое пр-во строк Рассмотрим множество матриц данного порядка над полем комплексных чисел, в которой строчки длины n; Строчки длины - вектор.
Эти строки образуют арифметич. пр-во ( “+” , “ А1-
А2-
А3- Если прибавить к строчке А4- Для любого вектора существует противоположный, и в сумме они дают 0 А5- λ А6- λ А7- λ А8 – 1 Аксиом задают, что арифметическое пр-во строк фиксированной длины Арифметическое=линейное=векторное Примеры: 1. Направленные отрезки (векторы), выходящие из начала координат на плоско-сти или в пространстве, являются (при фиксированнгой системе координат) соответ-ственно 2-мерными и 3-мерными векторами в смысле данного выше определения. 2. Коэффициенты всякого линейного уравнения с n неизвестными составляют n-мерный вектор. 3. Всякое решение системы линейных уравнений с n неизвестными есть n-мерный вектор. 4. Если дана матрица из s строк и n столбцов, то её строки являются n-мерными векторами, а столбцы - s-мерными векторами. 5. Сама матрица из s строк и n столбцов может рассматриваться как sn-мерный вектор (разными способами).
Сколько векторов в базисе- такой размер пр-ва Базис арифм. Пр-ва образует векторы этого же пр-ва, обладающие 3-мя св-ми: 1. Все пронумерованы 2. Эти векторы линейно независимы 3. Этих независимых вектором максимальное кол-во. Если взять векторов больше хотя бы на один, то система зависима.
Пусть дана система n-мерных векторов
Линейной комбинацией векторов (1) называется всякий n-мерный вектор вида
где λ1, λ2, ... , λr - произвольные числа, называемые коэффициентами линейной комбинации (2).(л.к.) Приравниваем Л.К. к 0. Если среди коэф. Есть хотя бы один не равный 0, то система линейно-зависима, а если с.к.=0 и все коэф. Равны 0, то система независима. Основные свойства линейной зависимости векторов. 1. Если один из векторов системы (1) является линейной комбинацией осталь-ных, то система (1) линейно зависима. 2. Если система векторов (1) линейно зависима, то хотя бы один из векторов этой системы линейно выражается через остальные. 3. Система, состоящая из одного вектора, линейно зависима тогда и только тогда, когда этот вектор нулевой. 4. Система, состоящая из двух векторов, линейно зависима тогда и только тогда, когда эти векторы пропорциональны. 5. Если часть (подсистема) системы векторов (1) линейно зависима, то и вся система (1) линейно зависима. 6. Если система векторов (1) линейно независима, то любая её пдсистема также линейно независима. Действительно, противное противоречило бы свойству 5. Из свойства 6 следует, что линейно независимая система не может содержать нулевого вектора или двух пропорциональных (в частности, равных) векторов. Теорема о базисном миноре Первые r-строк матрицы А линейно независимы, а строки, начиная с номера r+1. До p линейно независимы (через r первых строк выражается) Следствие 1. Мах кол-во линейно-независимых строк матрицы равно мах кол-ву линейно-независимых столбцов. Следствие 2. Для того, чтобы определитель был =0, необходимо и достаточно, чтобы его строки(столбцы) были линейно-зависимы (это означает, что ранг матрицы должен быть меньше порядка матрицы определителя)
Произвольные СЛАУ. Теория о совместности Кронекера-Капелли Произвольные СЛАУ Системой линейных алгебраических уравнений (СЛАУ) называется система вида:
Упорядоченный набор значений
· СЛАУ называется совместной, если она имеет решение, если решение одно. То матрица называется определенной, больше одного, то система - неопределенная. · СЛАУ называется несовместной, если не имеет решений. · СЛАУ называется однородной, если все правые части уравнений, входящих в нее, равны нулю одновременно.[AK1] Система называется квадратной, если количество уравнений равно количеству неизвестных.[AK2] Матричная запись систем уравнений: Исходную СЛАУ можно записать в матричном виде: A – Называется матрицей системы, это матрица, составленная из коэффициентов при неизвестных; B – Называетсявектором-столбцом неизвестных; X– Называется вектором-столбцом правых частейили свободных коэффициентов. Расширенной матрицейсистемы
|
|
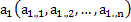
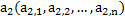
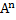 )
)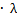 “- алгебраические операции, подчиняющиеся св-ам(аксиомам):
“- алгебраические операции, подчиняющиеся св-ам(аксиомам):
 – коммутативность
– коммутативность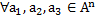
 –ассоциативность
–ассоциативность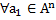
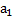 нулевую строку, получается
нулевую строку, получается 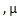
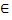 С
С )=( λ
)=( λ  - ассоциативность
- ассоциативность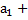
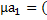 λ+
λ+ 
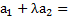 λ
λ 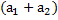
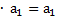
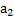 , ... ,
, ... ,  ,
,  . (1)
. (1)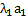 +
+  + ... +
+ ... + 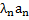 , (2)
, (2)
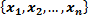 называется решением системы, если при подстановке в уравнения все уравнения превращаются в тождество.
называется решением системы, если при подстановке в уравнения все уравнения превращаются в тождество.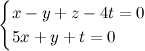
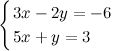 Система квадратная, так как неизвестных две и это число равно количеству уравнений системы.
Система квадратная, так как неизвестных две и это число равно количеству уравнений системы.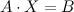 ,
,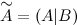 называется матрица, полученная из матрицы системы
называется матрица, полученная из матрицы системы  , дописыванием справа после вертикальной черты столбца свободных членов.
, дописыванием справа после вертикальной черты столбца свободных членов.