|
|
Прямая линия в пространстве и на плоскости.Прямая линия в пространстве. Линия в пространстве задается двумя поверхностями, т.е. является результатом пересечения этих поверхностей.
(задана линия в пр-ве)ψ(x, y, z)=0 ( 1. 1.Прямая линия.
( I )- общие уравнения
1. 2 ( I )
( L )
M(x, y, z) ( II )
1. 3. Если перейти от векторной формы к координатной, то: ( III ) y- z- ( III )- параметрические уравнения
Если дана система (I), то посмотрев алгебраическим глазом, то надо решить A=
Методом Краммера, задав произвольно
Направляющий вектор
Берем уравнение в конической форме
2.2 От параметрических( III ) к каноническим (IV)
y- z-
Пучок плоскостей Совокупность плоскостей, проходящих через одну и ту же прямую
П2 П1 (L)
П3
Задача: найти П3(ур-ие) На пл-ти П3 возьмем точку (М*) М*(x*, y*, z*) Пусть М*не принадлежит ( П2) 1) найдем две любые точки на прямой l ( решив систему (I)), взяв М* т эти точки, напишем ур-ие пл-ти, проходящей через эти точки. Пишем определитель 3-го порядка приравниваем к 0, получается уравнение. 2) а)запишем ур-ие пучка. Для этого умножим левую часть второго ур-ия системы(I) на множитель λ и составим комбинацию указанного вида для левых частей и приравниваем к 0. (V) ( Докажем, что (V)-это ур-ие, а не тождество. Док-во:
Выразив λ из равенств, получаем:
Посмотрев на полученный результат рассуждения от противного, получаем, что: Значит,( V)-это уравнение b)Это не просто ур-ие, а ур-ие первой степени, линейное, а всякое линейное ур-ие дает какую-то пл-ть.
(
Вывод: чтобы получить ур-ие пл-ти пучка пл-ти П3, надо взять ур-ие (V) и в него подставить λ* и получили ур-ие пл-ти:
Пл-ть П3 можно задать и так: искомая П3 ортоганальна (перпендикулярна) пл-ти П1 4. Прямая линия на пл-ти. Теория такая же как и в пр-ве. Теорема: Всякое уравнение 1. –ой степени вида (vI) Ax+By+C=0 на пл-ти задает прямую линию (ф) и обратно. Док-во Теорема состоит из двух частей. А) уравнение вида Пусть координаты точки Уравнение
Таким образом, уравнение Б) Всякая прямая в прямоугольной системе координат Oxy на плоскости определяется уравнением первой степени вида Пусть в прямоугольной системе координат Oxy на плоскости задана прямая a, проходящая через точку
|
|
 ( L) ϕ (x, y, z)=0 (
( L) ϕ (x, y, z)=0 (  )
) )
) (L)( I )
(L)( I ) 


 | |
| | 






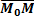 = t
= t  , t-всевозможные значения
, t-всевозможные значения ( II )-векторное уравнение
( II )-векторное уравнение
 x-
x- 
 t
t 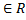
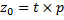





 1. 4 Если исключить параметр t из всех строк, то:
1. 4 Если исключить параметр t из всех строк, то:

 (L)
(L)  ( l )-число
( l )-число ( IV ) Каноническое уравнение
( IV ) Каноническое уравнение (Плоскость расположена || оси Z)
(Плоскость расположена || оси Z) (Плоскость расположена || оси X)
(Плоскость расположена || оси X)
 2.1 Как перейти от общих( I ) ур-ий к каноническим ( IV )
2.1 Как перейти от общих( I ) ур-ий к каноническим ( IV ) (из координат нормальных векторов)
(из координат нормальных векторов) 

 Найдем ранг матрицы
Найдем ранг матрицы Пусть δ(базисный минор) =
Пусть δ(базисный минор) =  = 0
= 0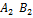

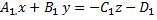
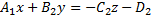
 , найдем какую-то точку.
, найдем какую-то точку.
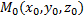
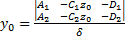
 равен векторному произведению
равен векторному произведению  и
и 

 =
=  =
= 
 =
=  =
= 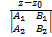

 x-
x-  =t
=t =t
=t =t
=t









 Если задано (П1)пересекает (П2) см.(I)-общие ур-ия прямой(L)
Если задано (П1)пересекает (П2) см.(I)-общие ур-ия прямой(L) П3
П3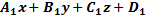 )+λ(
)+λ(  )=0
)=0
 λ
λ  =0
=0 λ
λ 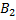 =0 (предположим, все коэф. Равны 0)
=0 (предположим, все коэф. Равны 0) λ
λ  =0
=0 ,
,  ,
, 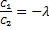
 =
=  =
=  , это значит, что
, это значит, что 

 c) нужна точка М*(нужна пл-ть, проходящая через М*). Подставим в ( V )М*, получаем:
c) нужна точка М*(нужна пл-ть, проходящая через М*). Подставим в ( V )М*, получаем: )+λ(
)+λ(  )=0 (не равно 0, не принадлежит П2)
)=0 (не равно 0, не принадлежит П2)
 Если точка принадлежит, то ее корд. Удовлетворяет ур-ию это пл-ти
Если точка принадлежит, то ее корд. Удовлетворяет ур-ию это пл-ти λ* = -
λ* = - 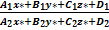
 )=0 это П3
)=0 это П3 задает прямую на плоскости.
задает прямую на плоскости. удовлетворяют уравнению
удовлетворяют уравнению  , то есть,
, то есть,  . Вычтем из левой и правой частей уравнения
. Вычтем из левой и правой частей уравнения  , при этом получаем уравнение вида
, при этом получаем уравнение вида  , которое эквивалентно
, которое эквивалентно  .
.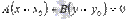 представляет собой необходимое и достаточное условие перпендикулярности двух векторов
представляет собой необходимое и достаточное условие перпендикулярности двух векторов  и
и  . То есть, множество всех точек
. То есть, множество всех точек  определяет в прямоугольной системе координат Oxy прямую линию, перпендикулярную направлению вектора
определяет в прямоугольной системе координат Oxy прямую линию, перпендикулярную направлению вектора  . Если бы это было не так, то векторы
. Если бы это было не так, то векторы  и
и  не были бы перпендикулярными и равенство
не были бы перпендикулярными и равенство  не выполнялось бы.
не выполнялось бы.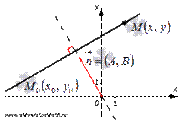
 задает прямую линию в прямоугольной декартовой системе координат Oxy на плоскости, следовательно, эквивалентное ему уравнение вида
задает прямую линию в прямоугольной декартовой системе координат Oxy на плоскости, следовательно, эквивалентное ему уравнение вида 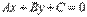 задает эту же прямую. На
задает эту же прямую. На .
. ,
,  - нормальный вектор прямой a, и пусть
- нормальный вектор прямой a, и пусть 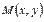 - плавающая точка этой прямой. Тогда векторы
- плавающая точка этой прямой. Тогда векторы  перпендикулярны, следовательно, их скалярное произведениеравно нулю, то есть,
перпендикулярны, следовательно, их скалярное произведениеравно нулю, то есть,  . Полученное равенство можно переписать в виде
. Полученное равенство можно переписать в виде  . Если принять
. Если принять  , то получим уравнение
, то получим уравнение  , которое соответствует прямой a.
, которое соответствует прямой a.