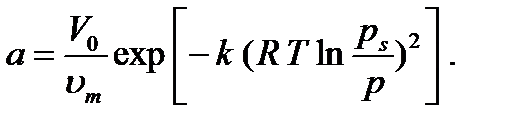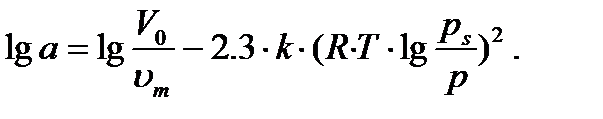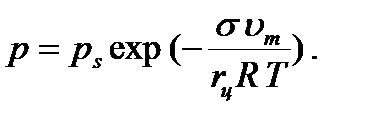|
|
Электролитпен коагуляциялау кинетикасы 6 глава2.8. Қатты дене – газ жанасу бетіндегі адсорбция 1. Лэнгмюрдің мономолекулалық адсорбция теориясы
Лэнгмюр теориясының басты алғы шарттары: 1) фазааралық бөліну бетінде тек мономолекулалық адсорбциялық қабат түзіледі; 2) адсорбент бетіндегі адсорбция орталықтары энергетика тұрғысынан біртекті, яғни бөліну беті эквипотенциалды деп саналады; 3) адсорбцияланған зат молекулалары беттік қабатта өзара әрекеттеспейді. Енді Лэнгмюр теңдеуінің кинетикалық жолмен қорытылып шығарылуын қарастырайық. Адсорбент бетіндегі адсорбция жүретін орындардың (адсорбция орталықтарының) жалпы санын N деп белгілейік. Егер де адсорбцияланған молекулалардың санын N1 деп есептеп, әрбір адсорбция орталығына бір молекула ғана адсорбцияланады деп қарастырсақ, онда бөліну бетіндегі бос адсорбциялық орталықтардың саны N0=N-N1 -ге тең болады. Адсорбция жылдамдығы бос адсорбция орталықтарының санына N0 және газ қысымына Р тура пропорционал: uа = kа×P×N0, (мұндағы kа – адсорбция жылдамдығының тұрақтысы). Ал десорбция жылдамдығы адсорбцияланған зат молекулаларының санына тура пропорционал болады: uд = kд×N1, (мұндағы kд – десорбция жылдамдығының тұрақтысы). Тепе-теңдік күй орнаған жағдайда uадсорб = uдесорб :
kа P N0 = kа P (N-N1) = kд N1. (1.1)
Мұндағы В = kа / kд. Бұдан q табатын болсақ,
(7.5) теңдеуді – Лэнгмюрдің мономолекулалалық адсорбция изотермасының теңдеуі деп атайды. Қысымның аз шамасында ВP<< 1 болады да, соңғы теңдеу сызықты теңдеуге (Генри заңы теңдеуіне) айналады:
V=Vмакс ×B×Р = К Р.
Ал қысымның өте жоғары шамасында BР >>1 болады да, адсорбцияланған газ көлемі тұрақты шамаға ие болады (7.1а-сурет): V = Vмакс. Лэнгмюр теңдеуіндегі тұрақты шамаларды анықтау үшін көбінесе (1.2) теңдеуді мынадай сызықты түрге келтіреді:
Сонда (р/V) –ның қысымға тәуелдігі түзу сызықты болады (1.1б-сурет). Осы түзу сызықтың ордината өсімен қиылысқан нүктесі 1/BVмакс– шамасына, ал оның абсцисса өсімен жасайтын бұрышының тангенсі tg a = 1/Vмакс- ға тең. Адсорбцияланған газдың максималь көлемін біле отырып, адсорбенттің меншікті бетінің ауданын (Sмен) да анықтауға болады:
Мұндағы V0- газдың бір моль мөлшерінің қалыпты жағдайдағы алатын көлемі, 22,4 л; NA –Авогадро тұрақтысы; S0 – қаныққан моноқабаттағы адсорбцияланған заттың 1 молекуласы алатын бетінің ауданы.
2.8 –сурет. Лэнгмюрдің адсорбция изотермасы (а) мен теңдеуінің сызықты түрінің (б) графигі
Газдар қоспасының адсорбциясында, Лэнгмюр теңдеуіне сәйкес, адсорбцияланған газдар көлемдері қосылады да, ал бос адсорбциялық орталықтардың саны көп құрамдасты қоспа үшін тұрақты болып қалады. Сонда газ қоспасының і-құрамдасының адсорбцияланған көлемі төмендегі теңдеу арқылы анықталады:
Бұл теңдеуге сәйкес газ қоспасындағы құрамдастың парциалдық қысымы артқан сайын, оның адсорбент бетіне ад-сорбцияланған көлемі (мөлшері) өсе түседі. Ленгмюр теориясы...-суретте көрсетілгендей сатылы адсорбциясын күрделенген нұсқасын да түсіндіруге мүмкіндік береді. Адсорбцияның мұндай сипатын бұл теория арқылы адсорбент бетінде активтілігі әр түрлі активтік орталықтардың болуымен түсіндіріледі. Адсорбцияның бірінші сатысында (I) активтілігі күштірек активтік орталықтардың толуына сәйкес келеді, ол қысымның салыстырмалы аз кезінде-ақ болады.Адсорбция изотерммиясының екінші сатысы (II) активтілігі төмен активтік орталықтардың толуына сәйкес келеді. Әрине ол суреттен көрініп тұрғандай жоғарырақ қысымдарда ғана болады. Жоғарыда айтылғандай Лэнгмюр теңдеуін энергетика тұрғысынан эквипотенциалды (біртекті) беттегі мономолекулалық адсорбцияға ғана қолдануға болады. Алайда, күнделікті өмірде кездесетін қатты (реалды) денелер беттері энергетика тұрғысынан біртекті болмайды. Сондықтан, теорияны реалды беттерге жарамды етіп түрлендіру үшін, адсорбент бетіндегі адсорбция орталықтарының энергетикалары әртүрлі екендігін ескеру керек. М.И.Темкин адсорбция жылуы мен беттің толтырылуы (q) арасында сызықты байланыс бар дей отырып, беттің біртексіз-дігін ескеретін мынадай адсорбция теңдеуін қорытып шығарды:
Мұндағы a- адсорбция орталықтарының энергиялары бойынша сызықтық таралуын сипаттайтын тұрақты шама; В0 – адсорбция ның максимальды жылуына сәйкес келетін Лэнгмюр теңдеуіндегі тұрақты; Р –газ қысымы. (1.6)-теңдеуді - адсорбцияның логарифмдік изотермасының теңдеуі деп атайды. Беттің орташа толтырылуы жағдайында, адсорбция жылуы мен беттің толтырылуы арасында логарифмдік байланыс бар деп қарастыратын болсақ, Фрейндлих-Бедекердің полимолекулалық адсорбция үшін эмпирикалық теңдеуін аламыз: А = K p 1/ n. (1.7)
Мұндағы А- газдың адсорбция шамасы (моль/г); р-қысым; K мен n-тұрақты шамалар. Соңғы теңдеуді логарифмдесек ол сызықты теңдеуге айналады:
1.2-сурет. Фрейндлих-Бедекер теңдеуінің түзу сызықты түрінің графигі
Демек,
2. Полянидің потенциалдық теориясы Полянидің потенциалдық теориясыполимолекулалық адсорбцияны сипаттайды.Бұлтеория адсорбция шамасы мен газ қысымы арасындағы байланысты адсорбциялық кеңістік көлемі арқылы қарастырады. Теория адсорбент бетінде беттік күштердің потенциалдық өрісі болады деген қағидаға негізделген. Адсорбциялық беттегі молекулалар арасында тек қана дисперстік күштер әсер етеді, ал дисперстік күштер аддитивті және температураға байланысты емес деген тұжырымдарға сүйенеді. Адсорбция барысында адсорбат молекулалары арасындағы әрекеттесу табиғаты өзгермейді, бірақ адсорбат молекулаларының беттегі тығыздығы (концентрациясы) артады деп қарастырылады. Адсорбциялық қабаттағы газды зат конденсацияланып, сұйық күйге өтеді. Бұның өзі адсорбциялық потенциалдың беттен қашықтыққа байланысын адсорбат көлемімен алмасты-руға мүмкіндік береді. Адсорбцияланған зат көлемін адсорция изотермасынан анықтауға болады (А = f (p/ps)):
V = A×Vм.(2.1) Мұндағы Vм- конденсирленген адсорбциялық қабаттағы адсорбаттың мольдік көлемі. Адсорбциялық қабаттағы молекулалар арасындағы әрекеттесудің өлшемі ретінде адсорбциялық потенциал (e) алынған. Адсорбциялық потенциал деп-адсорбент жоқ кезінде сұйық адсорбатпен тепе-теңдік күйдегі (қысымы рs) будың 1 моль мөлшерін адсорбентпен тепе-теңдік күйдегі бу фазасына (қысымы р) көшіру үшін атқарылатын жұмыс шамасын айтады:
(2.2)
Демек, тәжірибелік мәндерден адсорбцияланған газдың (конденсаттың) көлемін (V)жәнеадсорбциялық потенциалды (e) анықтайды. Сонан соң адсорбцияның потенциалдық қисы-ғын, яғни e = f (V) қисығын тұрғызады (2.1-сурет). Потенциалдық қисықтың түрі температураға тәуелсіз. Өйткені адсорбциялық қабатта орын алатын дисперстік күштер температураға байланысты емес.
2.1-сурет. Адсорбцияның сипаттамалық потенциалдық қисығы
Сондықтан әртүрлі температураларда алынған тәжірибелік мәндер бір потенциалдық қисық e = f (V) бойында жатады, яғни
Демек әртүрлі екі температура үшін былай жазуға болады:
V = A1×Vм,1= A1×Vм,1; e = R×T1×ln (ps,1/p) = R×T2××ln (ps,2/p). (2.3) Демек, бір температурадағы изотерманы біле отырып, екінші температурадағы изотерманы анықтауға болады. М.М.Дубининнің пікірі бойынша бір адсорбент бетіне әртүрлі адсорбаттар адсорбцияланатын болса, онда адсорбаттың кез-келген көлемінде адсорбаттардың адсорбциялық потенциал-дарының қатынасы тұрақты шамаға (b) тең болады:
(e / e0 )v = b. (2.4)
Мұндағы e0 – стандарт ретінде алынған адсорбаттың адсорбциялық потенциалы. bкоэффициентінаффиндік эффициент деп атайды. Демек, бір адсорбат үшін сипаттамалық қисықты және аффиндік коэффициентті білетін болсақ, онда екінші адсор-баттың сол адсорбент бетіне адсорбциясын есептеуге болады.
3. Полимолекулалық адсорбция изотермасының БЭТ теңдеуі Жоғарыда айтылғандай, Лэнгмюр теңдеуін тек мономолекулалық адсорбцияға қолдануға болады. Мономолекулалық адсорбция хемосорбция барысында, қысымы оншалықты үлкен емес және температурасы кризистіқ (дағдарыстық) нүктеден жоғары жатқан газдың адсорбциясы кезінде байқалады. Тәжірибе көрсеткендей, адсорбенттердің бетіне газ немесе бу адсорбцияланғанда көп жағдайда полимолекулалық адсорбциялық қабат түзіледі. Жалпы газ бен бу адсорбциясы кезінде 5 түрлі изотерма қисықтарының біреуінің болу мүмкін екендігі тәжірибе жүзінде анықталған (3.1-сурет). I-қисық – Лэнгмюр теңдеуіне бағынатын адсорбция изотермасы; II-қисық – S-пішінді, қысымның салыстырмалы орта мәнінде тұрақты қалатын, адсорбция изотермасының қисығы; III-қисық – қысым артқан сайын бір-тіндеп өсетін адсорбция изотермасының қисығы; IV- және V-қисықтар – адсорбция барысында капиллярлық конденсация байқалатын күрделі полимолекулалық адсорбция изотермасының қисықтары. Полимолекулалық адсорбцияны сандық жағынан сипаттайтын бірнеше теориялар бар. Алайда олардың арасындаполимолекулалық адсорбция құбылысын біршама дәлірек сипаттайтын теория болып Брунауэр, Эммет және Теллер жасаған теория саналады. Бұл теорияны қысқаша БЭТ теориясы (авторлар фамилияларының бас әріптерінен құралған) деп атайды. БЭТ теориясының басты алғы шарттары: 1) адсорбент беті біртекті; 2) адсорбент бетіне адсорбцияланған газ молекулалары өзара әрекеттеспейді; 3) адсорбент бетінде бірнеше адсорбциялық қабаттар түзілуі мүмкін, яғни газдың қатты дене бетіндегі адсорбциясы полимолекулалы және 4) бірінші адсорбциялық қабат түзіліп болмас бұрын екінші және үшінші қабаттар түзілуі мүмкін.
3.1-сурет. Газ бен будың адсорбция изотермалары
Осы алғы шарттарға сүйене отырып, теория авторлары адсорбцияланған газ көлемі (V) мен оның қысымы (Р) арасындағы байланысты өрнектейтін мынадай теңдеуді қорытып шығарды:
Мұндағы Р0 – газдың қаныққан буының қысымы; Vмакс –адсорбцияланатын газдың максималь көлемі; С- тұрақты шама, оның мәні мономолекулалық адсорбцияның тепе-теңдік тұрақтысының будың конденсациялану константасына қатынасы арқылы анықталады. (3.1) теңдеуді –БЭТ-ң полимолекулалық адсорбция теңдеуі деп атайды. Тәжірибелік мәндерді өңдегенде, көбінесе БЭТ теңдеуін түзу сызық теңдеуі түрінде пайдаланады:
График тұрғызу арқылы теңдеудегі Vмакс және С тұрақты шамаларды анықтауға болады. Ол үшін
3.2 -сурет. БЭТ-ң полимолекулалық адсорбция теңдеуінің түзу сызықты түрінің графигі
Газ қысымы аз болғанда, яғни P/P0<< 1 жағдайында‚ БЭТ теңдеуі Лэнгмюр теңдеуіне айналады:
Мұндағы: KР=С/Р0 - мономолекулалық адсорбцияның тепе-теңдік константасы. Демек, Лэнгмюрдің мономолекулалық адсорбция теңдеуі БЭТ теңдеуінің дербес түрі болып саналады. Жалпы БЭТ теңдеуі салыстырмалы қысымның 0,05 < Р/Р0 < 0‚3 мәндері аралықтарында газ адсорбциясын біршама дәл өрнектейді. Өйткені Р/Р0 < 0‚05 болғанда қатты дене бетінің әртектігі сезіліп, теңдеуге әртектілікті ескеретін түзету коэффициентін енгізуге тура келеді. Ал үлкен қысым жағдайында, яғни Р/Р0 > 0‚3 болғанда, беттегі адсорбцияланған газ молекулаларының өзара әрекеттесуі күшейе түседі. БЭТ теориясында адсорбент беті біртекті деп қарастырылады және беттік қабаттағы газ молекулаларының өзара әрекеттесуі ескерілмейді. Соған қарамастан, практикада БЭТ теңдеуі ұсақ қатты заттардың меншікті бетінің ауданын (дисперстігін) анықтау үшін кеңінен қолданылады. Ол үшін адсорбат ретінде инертті газды (азот, аргон, криптон, т.б.) алып, оның берілген ұсақ адсорбент бетіне адсорбцияланған максималь көлемін тәжірибе жүзінде анықтайды. Сонан соң, белгілі теңдеу арқылы адсорбенттің меншікті бетінің ауданын Sмен (м2/г) есептейді:
S мен = (Vмакс NA S0)/ V0 . (3.4) Мұндағы Vмакс – адсорбенттің бірлік массасында адсорбцияланған газдың максималь көлемі; NA – Авогадро тұрақтысы; V0 – қалыпты жағдайдағы газдың 1 моль мөлшерінің алатын көлемі; S0 – газ молекуласының адсорбциялық қабатта алатын бетінің ауданы.
4. М.М.Дубининнің адсорбция теңдеуі М.М.Дубинин микрокеуек адсорбенттер (кеуектер радиусы 30×10 -10 м-ден аспайды) үшін мынадай си-паттамалық қисық теңдеуін ұсынды:
V = V0 ×exp (-k×e2). (4.1) Мұндағы V – адсорбцияланған газ конденсатының көлемі; V0- адсорбцияланған газ конденсатының максимал көлемі, сан жағынан микро кеуектерінің көлеміне тең; k-эмпирикалық тұрақты шама; e-адсорбциялық потенциал; Жоғарыдағы теңдеу негізінде адсорбция шамасы (а) мен газ қысым арасындағы байланысты өрнектейтін теңдеу алынды:
(4.2)
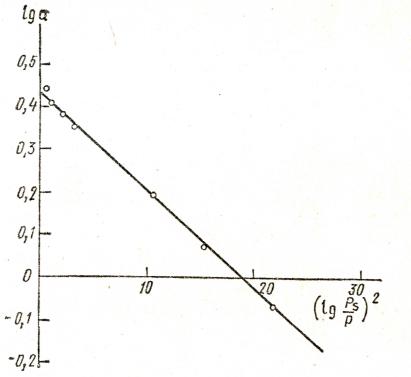
Мұндағы p – газ қысымы; ps – газдың қаныққан қысымы; um – газдың мольдік көлемі. Адсорбцияланған газ конденсатының максимал көлемін (микрокеуектер көлемін) анықтау үшін lg a = f [lg (ps /p)2]түзу-ін тұрғызады (4.1-сурет). Егерде соңғы теңдеуді логарифмдесек сызықты теңдеу аламыз:
(4.3)
Осы түзудің ордината өсімен қиылысу (lg (ps/p2)=0 болғанда) нүктесі lg(V0/um) шамасына тең болады. Бұдан V0 мәнін есептейді.
4.1-сурет. М.М.Дубинин теңдеуіндегі тұрақты шамаларды графикалық жолмен анықтау
5. Кеуек қатты денелерде газдың (будың) адсорбциясы
Кеуек қатты денелерде газ адсорбцияланғанда көп жағдайда капиллярлық конденсация құбылысы да қатар жүреді. Капиллярлық конденсация деп жазық бет үстіндегі қаныққан бу қысымымен (ps) салыстырғанда газдың кеуек қатты дене-дегі конденсациялану қысымының (р) азаюын айтады. Қысымдар қатынасының (р/ps) аз мәнінде қатты дене қуыстарының қабырғаларында конденсат түзіледі. Егерде сұйық кеуек бетіне жұғатын болса, онда сұйық беті майысады да ойыс бет түзіледі. Ойыс бет үстіндегі қаныққан бу қысымы жазық бет үстіндегі қаныққан бу қысымынан әрқашан аз. Сондықтан кеуек заттарда будың конденсациялануы қысымның р/рs<1 мәндерінде басталады. Бу қысымы мен беттің қисықтылық радиусы арасындағы байланыс Томсон (Кельвин) теңдеуі (5.56) арқылы сипатталады. Сонда сұйықтың қатты дене бетіне жұғуы (q <90o) жағдайында Томсон (Кельвин) теңдеуі 1) Шар тәріздіс мениск үшін былай жазылады:
(5.1)
Мұндағы rш-шар тәріздес менискінің қисықтылық радиусы; um мен s -адсорбцияланған заттың (адсорбтивтің) мольдік көлемі мен беттік керілуі. 1) Ойыc цилиндрлік мениск үшін былай жазылады:
(5.2) Мұндағы rц- цилиндрлік менискінің қисықтылық радиусы. Демек, rш = rц жағдайында pш< pц.
Көп жағдайда адсорбенттер құрамындағы қуыстардың пішіндері күрделі болып келеді. Соған байланысты кеуек адсорбенттердегі газдың адсорбция изотермасы мен капиллярлық конденсациясы да әртүрлі болады (5.1-сурет).
5.1-сурет.Пішіндері әртүрлі кеуек қатты денелердегі адсорбция изотермалары
Конус тәріздес кеуек қатты денелерде (5.1а-сурет)қысымның аз аймағында газдың адсорбциялануы барысында кеуек қабырғаларында жұқа сұйық қабат түзіледі. Пайда болған сұйық кеуек түбіне ағып жиналады. Егерде сұйық кеуек бетіне жұғатын болса, онда оның беті майысады да, нәтижесінде ойыс бет (мениск) пайда болады. Кеуек сұйықпен толтырылған сайын беттің қисықтылық радиусы өсе түседі де, нәтижесінде адсорбаттың конденсациялану қысымы кемиді. Бұның өзі сайып келгенде адсорбцияның артуына әкеледі. Кері құбылыс - десорбция - адсорбция қисығы бойымен кері жүреді. Бір жағы бекітілген цилиндр тәріздес кеуектерде (5.1б-су-рет)қысымның аз аймағында газдың кеуек бетіне адсорбцияланып конденсациялануы барысында цилиндрдің жабық түбіне сұйық жиналады. Кеуек бетіне сұйықтың оң жұғуы байқалғанда сұйық беті оң қисаяды да, ойыс шар тәріздес мениск пайда болады. Беттің қисаюы капиллярлық қысымның төмендеуіне себеп болады, адсорбция шамасы артады. Конденсация барысында сұйық бетінің қисықтылық радиусы өзгермейтіндіктен, адсорбцияның шамасы тұрақты қысым жағдайында вертикаль түзу бойымен күрт өседі (5.5б-сурет). Ал десорбция құбылысы адсорбция қисығы бойымен кері бағытта жүреді. 3)Екі жағы да ашық цилиндр тәріздес кеуекте(5.1в-сурет) қысымның аз мәнінде кеуек қабырғаларында сұйық адсорбция-лық қабаттар түзіледі де, нәтижесінде цилиндр тәріздес ойыс бет пайда болады. Қысымның шамасы қаныққан қысым мәніне жеткенде капиллярлық конденсация басталады да, нәтижесінде кеуек қабырғасындағы сұйық қабаттың қалыңдығы арта түседі, менискінің қисықтылық радиусы кемиді. Адсорбтивтің конденсациялануы қысымның тұрақты мәнінде жүреді де, кеуек толығымен сұйықпен толтырылғанда цилиндр тәріздес кеуектің ашық екі жағында шар тәріздес менискілер пайда болады. Қысымды одан ары қарай арттырғанда шар тәріздес менискілер үстіне будың белгілі бір мөлшері конденсацияланады, нәтижесінде менискінің қисықтылық радиусы нольге дейін кемиді. Десорбция кезіндебастапқыда процесс қайтымды болып саналады, булану барысында шар тәріздес менискінің қисықтылық радиусы арта түседі. Ары қарай қисықтылық радиусы тұрақты шар тәріздес мениск бетінен сұйықтың булануы жүреді. |
|
 -адсорбент бетінің моноқабатпен жабылған бөлігінің үлесі екендігін еске алсақ, онда жоғарыдағы теңдеуді былайша түрлендіре аламыз:
-адсорбент бетінің моноқабатпен жабылған бөлігінің үлесі екендігін еске алсақ, онда жоғарыдағы теңдеуді былайша түрлендіре аламыз: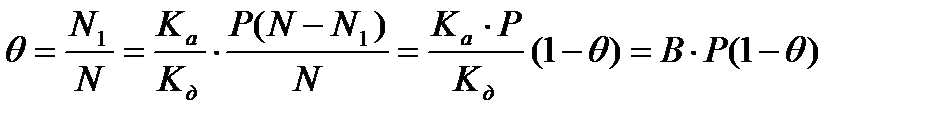 .
. . q-ны V/ Vмакс мәнімен (V- адсорбцияланған газдың көлемі; Vмакс - газдың адсорбцияланатын газдың максимал көлемі) алмастырған кезде, адсобцияланған газ көлемінің қысымға тәуелдігін өрнектейтін теңдеуді аламыз:
. q-ны V/ Vмакс мәнімен (V- адсорбцияланған газдың көлемі; Vмакс - газдың адсорбцияланатын газдың максимал көлемі) алмастырған кезде, адсобцияланған газ көлемінің қысымға тәуелдігін өрнектейтін теңдеуді аламыз: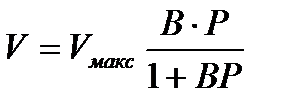 . (1.2)
. (1.2)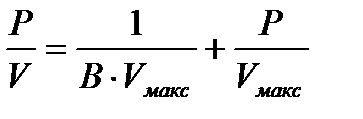 (1.3)
(1.3) . (1.4)
. (1.4)
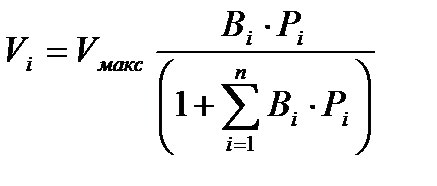 (1.5)
(1.5) . (1.6)
. (1.6) . (1.8)
. (1.8)
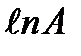 мен
мен  арасында түзу cызықты байланыс бар (1.2-cурет). Түзу сызықтың ордината өсімен қиылысқан нүктесі
арасында түзу cызықты байланыс бар (1.2-cурет). Түзу сызықтың ордината өсімен қиылысқан нүктесі 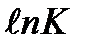 -ға тең де, ал оның абсцисса өсімен жасайтын a бұрышының тангенсі tg a =1/n –ге тең болады.
-ға тең де, ал оның абсцисса өсімен жасайтын a бұрышының тангенсі tg a =1/n –ге тең болады.

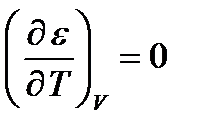

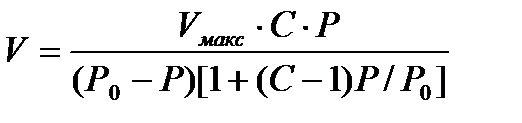 . (3.1)
. (3.1) . (3.2)
. (3.2)
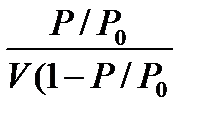 мен (Р/Р0) мәндері арасындағы байланысты көрсететін график тұрғызады (3.2-сурет). Сонда түзу сызықтың ордината өсімен қиылысқан нүктесі 1/ Vмакс С мәніне, ал түзу сызықтың абсцисса өсімен жасайтын a бұрышының тангенсі
мен (Р/Р0) мәндері арасындағы байланысты көрсететін график тұрғызады (3.2-сурет). Сонда түзу сызықтың ордината өсімен қиылысқан нүктесі 1/ Vмакс С мәніне, ал түзу сызықтың абсцисса өсімен жасайтын a бұрышының тангенсі  мәніне тең болады.
мәніне тең болады. . (3.3)
. (3.3)