|
|
Электролитпен коагуляциялау кинетикасы 9 главаКөбіне реал денелердің деформациясы кезінде релаксация құбылысымен қатар кешіккен серпімділік атты құбылыс байқалады. Релаксация серпімді деформацияның пластикалыққа ауысуына әкелсе, кешіккен серпімділік толығымен серпімді деформация тез арада пайда болмауымен байқалады (идеал қатты денелердегідей). Бұл деформацияның жартысы серпімді деформация берілген кернеуге сәйкес келетін мәнге тек қана белгілі уақыт аралығынан кейін жететіндей уақыт бойынша дамиды. Кешіккен серпімділік, неғұрлым қатты дененің құрылымы біртексіз болса, соғұрлым күштірек байқалады. Шын серпімділігі бар қатты тәріздес микрогетерогендік және коллоидтық жүйелердің механикалық қасиеттерін қарастыруға оралайық. Мұндай жүйелерге поликристалды металдар, әртүрлі құрылымданған дисперстік жүйелер, сірнелер,
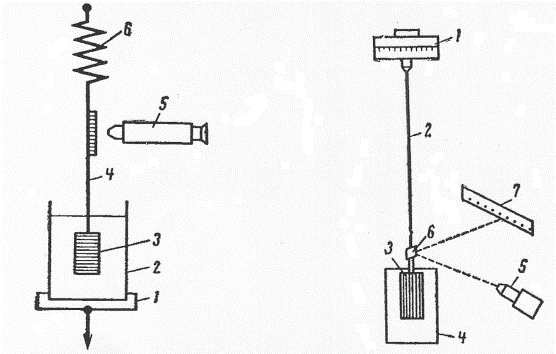
Алайда құрылымдық тордың бұзылуына әкелетін кернеулерде бұл жүйелер тұтқыр сұйықтықтар секілді аға алады, сонымен қатар олардың тиімді тұтқырлығы ағудың жылдамдығы немесе кернеудің өсуімен әрдайым азаяды. Көп жағдайларда мұндай жүйелердің деформациясы кезінде серпімді (лездік) деформация, кешіккен серпімділік және ағу құбылыстары бір-біріне уақыт арасындағы жалпы деформацияның өзгерісінің 2.8 - суретте көрсетілген сипаттамалы көрінісін береді. Одан деформациялайтын күштің әсерінен, мысалы Р ығысу кернеуінің τ1 уақытта жүйеге әсер еткен кезде ε1 лездік серпімді деформация дамитының байқаймыз. Бұл деформацияға лездік ығысу модулі сәйкес келеді Е1=Р/ε1. Сонан соң құрылымдық элементтердің қайтымсыз қайта топтасуының нәтижесінде жүйе аға бастайды. Сонымен қатар жүйеде құрылымдық элементтердің қайтымды қайта топтасуының нәтижесінде ε2 деформациясына жағдай жасайтын, кешіккен серпімділік дами бастайды. Бұл баяу дамитын серпімді деформацияға Е2=Р/ε2 ығысу модулі сәйкес келеді. Мұның бәрі 2.8-суретінде көрсетілгендей қисықтың, жүйенің ағуына сәйкес келетін, қандайда бір сызыққа асимптотикалық жақындауына әкеледі. Егер бірқатар уақыттан кейін τ2 кезінде деформациялаушы күш алынып тасталса, ε1 серпімді деформация дыбыс жылдамдығымен жоғалып кетеді. Сонан соң біртіндеп кешіккен серпімділікпен жағдай жасалған ε2 деформациясы жоғалады, ал ағумен (шын релаксациямен) жағдай жасалған ε3 деформациясы қайтымсыз болып қалады. Кейде осы жағдайларда табылған қайтымсыз деформация шын пластикалық емес, пластикалық сияқты байқалынатын деформация болып келеді, ол деформацияланған дененің қайта қалпына келу үдерісі өте баяу жүруінің салдарынан болады. Соңғы жағдайда қалдық деформация ішінара немесе толығымен, құрылымдық элементтердің тезірек қайта топтасуына жағдай жасайтын дененің белгілі өңдеулерінен кейін (мысалы, қыздыру немесе еріткіште ісіну) жойылады. Бұл сырттан берілетін жүктемені алып тастағаннан кейін деформацияланған дененің жасырын серпімділігінің болуын көрсетеді. Серпімділік, яғни дисперстік жүйенің деформациялаушы күштің әсерін тоқтатқаннан кейін бастапқы пішініне оралу қабілеті, жүйенің ерекше құрылымы бар екенін көрсетеді, ол құрылым элементтерінің бір-біріне қатысты ығысуына кедергі жасайды. Коллоидтық жүйелердің механикалық қасиеттерін анықтау. Жеткілікті механикалық беріктігі бар қатты жүйелерді әдеттегі физика-механикалық талдау әдістерімен (кернеу деформациясына тәуелділікті сипаттайтын қисықты алу, созу немесе ығысу кезіндегі шекті кернеуді анықтау, қатынасты және қалдық деформацияны анықтау және т.б.) зерттеуге болады. Бұл кезде тек қана деформациялау жылдамдығын ескеру керек, себебі ол алынған нәтижелерге қатты әсер етеді. Сірнелердің және басқа да құрылымданған дисперстік жүйелердің серпімділік байқататын механикалық қасиеттерін анықтайтын бірқатар арнайы әдістері бар, біз оның екеуін ғана қарастырамыз. Пластинканы тангенсиальды ығыстыру әдісі. С.Я. Вейлер мен П.А. Ребиндер ұсынған бұл әдістің принципі зерттелетін жүйеге салынған пластинканы ығыстыруға қажет күшті анықтауда жатыр. Өлшеу жүргізілетін құрал 2.9-суретте көрсетілген.
Тік бұрышты рифтелген пластинка 3 қатты жіп 4 көмегімен пружиналы динамометрге 6 ілінген. Зерттеудің алдында 2 кюветаға құйылған, дисперстік жүйеге пластинканы толығымен батырады. Дисперстік жүйесі бар кюветаны көтерілетін орындықшаға 1 орнықтырады. Кюветасы бар орындықты түсіргенде пружина созылады да, жүйеде ығысу кернеуі пайда болады, ол пружинаның созылуына пропорционалды. Оны окулярлы микрометрі немесе микрошкалксы бар микроскоппен 5 өлшеуге болады. Р ығысу кернеуін алдын ала калибрленген серіппенің созылуымен және осы созылуға сәйкес келетін Ғ күшпен мына теңдеу бойынша есептейді: Р=Ғ/(2s) (2.15) мұнда s-пластинканың (3) бір жақ беті. Жүйенің құрылымының беріктігін сипаттайтын және ең көп күшке (пластинка бетімен жүйенің сырғанауы болмағанда) сәйкес келетін ығысу θ шекті кернеуін мына теңдеумен табады: θ =Fмакс/(2s) (2.16) Суреттелген құралдың көмегімен тек ығысудың шектік кернеуін ғана емес, сондай-ақ серпімділік модулін, эффективті тұтқырлықты анықтауға, релаксация үдерісін зерттеуге және де деформацияның әртүрлі жылдамдықтарында ε, Р толық деформациялық қисықтарды алуға болады. Цилиндрді айналдыру әдісі.Серпімді жіпке ілінген және зерттелетін жүйеге орналастырылған цилиндрді айналдыру арқылы құрылымданған жүйелердің серпімді-пластикалық қасиеттерін анықтау әдісін ең әуелі 1889ж. 2.10-суретте Ф.Н. Шведов ұсынған анықтау жүргізілетін құралдың сұлбасы келтірілген. Құралдың серпімді жіп 2 орнатылған орағыш басы 1 бар, жіпке айнасы бар 6 рифтелген цилиндр 3 ілінген. Цилиндр 3 зерттелетін жүйесі бар кюветаға 4 толығымен батырылған. Орағыш басты белгілі α бұрышқа бұрғанда орағыш момент цилиндрге жіп арқылы беріледі де, цилиндрді айналдырған жүйе қабатында ығысу деформацияларын тудырады. Цилиндрде жіптің серпімді кернеуі мен деформацияланған жүйенің кедергісі арасындағы тепе-теңдікке дейін β бұрышқа бұрылады. (α-β) айырымы орағыш бас беретін белгілі Ғ күшке сәйкес келетін жіптің айналу бұрышын ω береді. Цилиндрдің айналу бұрышын 5 жарықтандырғыш жіберетін жарық сәулесінің ығысуымен және оның 6 айнадан 7 шкалаға шашырауынан өлшейміз. Сипатталған құрал берілген тұрақты кернеу әсер еткеннен кейін ығысу деформациясының даму кинетикасын және жүктемені алып тастағаннан кейінгі деформацияның құлау кинетикасын зерттеуге өте қолайы. Комплексті эластовискозиметр деп аталған приборды А.А. Трапезников құрастырған. Ол әртүрлі жұмысшы ұяшықтар (коаксиалды цилиндрлер, конус, диск) қолдануға және зерттеудің әртүрлі әдістерін қолдануға мүмкіндік береді.
2.5 Коллоидтық жүйелердің тұтқырлықтарының дисперстік фазаның концентрациясына тәуелділігі Коллоидтық жүйелердің тұтқырлығы таза дисперсиялық ортаның тұтқырлығынан әрдайым жоғары. 1906ж. Эйнштейн тек гидродинамикалық көзқарастардан жүйенің η тұтқырлығы мен дисперстік фазаның концентрациясы арасындағы байланыстыратын теңдеуді шығарған: η=η0 (1+2.5 φ) (2.17) мұнда η0-дисперсиялық ортаның тұтқырлығы, φ-дисперстік фазаның көлемдік концентрациясы. (2.17) теңдеуі сұйықтықтағы жүзгін бөлшектер қатты шар тәрізді денелер болады деген жағдайда дисперстік фазаның концентрациясы салыстырмалы аз және бөлшектер арасында әрекеттесу болмайтын жағдайда ғана қолданылады. Сондай-ақ Эйнштейн теңдеуі сақталу үшін жүйе қысылмайтын болуы керек, сұйықтықтың ағуы ламинарлы сипатта болуы және бөлшектермен сұйықтық арасында сырғанау болмауы керек, ең ақырында бөлшектер ортаның молекулаларының еркін жүгіруімен салыстырғанда үлкен, бірақ ағу болатын кеңістікпен салыстырғанда аз болуы керек. (2.17) теңдеудегі сандық коэффициенттің мәні бөлшектің пішініне тәуелді. Сондықтан Эйнштейн теңдеуін жалпы түрде былай көрсетуге болады: η=η0 (1+α φ) (2.18) мұнда α-бөлшектердің пішініне тәуелді көбейткіш. Эйнштейн теңдеуін көбіне былай жазады: (η/η0)-1=(η-η0)/η0=αφ=α(nυ/V) мұнда η/η0-жүйенің тұтқырлығының орта тұтқырлығына қатынасы (салыстырмалы), n-жүйедегі бөлшектердің жалпы саны, υ-дисперстік фазаның бір бөлшегінің көлемі, V-жүйенің көлемі, мл. Дисперсиялық ортаға дисперстік фазаның белгілі мөлшерін қосқандағы оның тұтқырлығының қатынасты ұлғаюын сипаттайтын (η-η0)/η0 шамасын көбінесе меншікті тұтқырлық деп атауды. Оны көбіне ηменш деп белгілейді. Алдынғылардан: ηменш=ηсал-1=αφ (2.19) Осылардан Эйнштейн бойынша жүйенің тұтқырлығы мен ондағы дисперстік фазаның арасында түзу сызықты тәуелділік болады. Сондай-ақ Эйнштейн бойынша тұтқырлық жүзгіннің дисперстілігіне тәуелсіз. Эйнштейн теңдеуін эксперименталды тексеруді Банселен гуммигут жүзгіндерінде, Оден күкірт кірнелерінде және Эйрих шыны шариктерінде және ашытқы жасушаларының, саңырауқұлақтардың шар тәрізді (жүзгіндерінде) жүргізген. Барлық зерттеулерде бөлшектердің сфералық пішінінде және дисперстік фазаның аз концентрациясында φ кезінде сандық коэффициент 2.5 жуық болған. Ауытқулар бөлшектердің шар тәрізді емес, дисперстік фазаның жүзгіндегі концентрациясы байқалатындай және бөлшектер арасында электрлік және басқа да әрекеттесу күштері болғанда ғана байқалған. Бөлшектердің анизодиаметрлігінің әсері. Таяқша, эллипсоид немесе пластинка тәріздес бөлшектері бар жүзгіннің тұтқырлығы Эйнштейн теңдеуіне сәйкес болатыннан әрдайым жоғары болады. Мұның себебі қарқынды броундық қозғалыста болатын шар тәріздес емес бөлшектердің айналасында түзілетін көлемге (айналу эллипсоиды) түсетін сұйықтық бөлшекпен байланысты сияқты болатынында. Осының нәтижесінде тұтқырлықтың өсуіне әкелетін жүйедегі дисперстік фазаның көлемдік үлесінің солай байқалатындай өсуі пайда болады. Тәжірибелік жолмен қарқынды броундық қозғалыста болатын анизодиаметрлігі аз бөлшектері бар жүзгіндердің тұтқырлығы эллипсоидты айналудың үлкен және кіші осьтерінің қатынасының квадратына пропорционалды өсетіні, ал баяу броундық қозғалыста болатын үлкен шар тәрізді емес бөлшектері бар суспензиялардың тұтқырлығы тек осьтердің қатынастарына тура пропорционалды өсетіні анықталды. Кун, Симха және басқа да зерттеушілердің әртүрлі пішінді бөлшектердің моделін қолданған теориялық есептеулері өте күрделі және сенімсіз. Сондықтан осы күнге дейін коллоидтық жүйенің бөлшектер пішініне тәуелділігінің жалпы теориясы жоқ. Анизодиаметрлік бөлшектері бар жүйелердің тұтқырлығы ағу жылдамдығына тәуелді. Созылыңғы бөлшектер ағыста бағытталады, олардың айналу қозғалысы қиындайды да, соның нәтижесінде ағудың жылдамдығының өсуімен жүйенің тұтқырлығы азаяды. Мұндай құбылыстарды мысалы, қатты анизодиаметрлік бөлшектері бар V2O5 кірнелерінің тұтқырлықтарын өлшегенде байқауға болады. Дисперстік фазалардың шын концентрациясы мен сольваттаудың әсері.Эйнштейн теңдеуінен шығарылған тұтқырлықтың мәнінен концентрлі дисперстік жүйенің тұтқырлықтарының айырмашылығын сұйықтықта бөлшектердің айналасында жүйенің қозғалысын қиындататын өзара қоздырушы микроағыстардың пайда болуымен түсіндіреді. Дебройн гидродинамикалық әрекеттесулермен қатар механикалық әрекеттесуді (бөлшектердің соқтығысуы, будың түзілуі және т.б.) ескеру керек екенін айтты. Жүзгіндердің өте аз концентрациялары кезінде бір бөлшектердің айналасында пайда болатын ағыс басқа бөлшектердің айналасында пайда болатын ағыстарға және сұйықтықтың барлық ағыстарының қозғалу жылдамдықтарына өте аз әсер етеді. Алайда дисперстік фазаның концентрациясының өсуімен бұл әсер өсе береді де, Эйнштейн заңынан ауытқуға әкеледі. Эйнштейн теңдеуімен табылған мәндерден дисперстік жүйенің тұтқырлығының ауытқуын бөлшектердің сольваттануымен де түсіндіруге болады. Сольватация құбылысы дисперстік фазаның бірдей көлемдік концентрациясында тұтқырлықтың дисперстік жүйеден байқалатын тәуелділігін де түсіндіре алады. Сольваттану әсерін былай көрсетуге болады. Егерде r радиусты шар тәрізді бөлшектің бетіне h қалыңдығы бар дисперсиялық ортаның қабаты жабысып қалса, онда тұтқырлыққа әсер ететін бөлшектердің тиімді көлемі (бөлшектердің сольваттық қабаттарының көлемімен бірге көлемі) 4/3π(r+h)3. r-мен салыстырғанда кіші h мәндері үшін 4/3π(r3+3r2h) болады. Осыған сәйкес дисперстік фазаның тиімді көлемдік концентрациясын φ есептегенде дисперстік фазаның көлемі ретінде 4/3πr3ν емес 4/3π(r3+3r2h)ν (мұнда ν-сандық коцентрация) шамасын алу керек. Егер дисперстік фазаның шын көлемі ретінде
соған байланысты φ шамасы φ0 дисперстік фазасының көлемінен үлкен болады және бұл шама бөлшектер аз болған сайын көп болады. Басқа сөзбен айтқанда, тұтқырлық кірне бөлшектерінің мөлшері өсуімен ұлғаяды. Мұндай күкірт кірнесінің дисперстік дәрежесінің өсуімен тұтқырлықтың ұлғаюын Свен Оден байқаған. Фикенчер мен Марк сольваттанудың әсерін есепке алу үшін Эйнштейн теңдеуін модифицирлеуді ұсынды, оған сәйкес түзетулер енгізу керек. Бұл авторларға сәйкес Ван-дер-Ваальс теңдеуіндегідей Эйнштейн теңдеуінде жүйенің жалпы көлемінің орнына тиімді көлемді енгізу керек, яғни жүйенің көлемінен бөлшектер көлемін алып тастау арқылы. Жүйедегі бөлшектердің сольваттанған күйде және броундық қозғалыста болатындықтан қандай да айналу денелерін суреттегенде, бөлшектермен энергетикалық және стерикалық байланысқан дисперсиялық ортаның көлемін дисперстік фазаның көлеміне қосу керек. Сонда (2.18) теңдеуі мына түрге келеді:
мұнда υ' ортамен энергетикалық және стерикалық байланысқан бөлшектердің көлемі . Фикенчер және Марк теңдеуі неліктен бірқатар жағдайларда дисперстік фазаның концентрациясының өсуімен тұтқырлықтың артуының түзу сызықты тәуелділікке сәйкес болатынға қарағанда тез болуын жақсы түсіндіреді. Шынында да ерітіндідегі дисперстік фазаның концентрациясының өсуімен алымындағы n шама оған пропорционалды өседі де, сонымен қатар, бөліміндегі Бөлшектер арасындағы әрекеттесулердің әсері. Эйнштейн теңдеуінің бірқатар жағдайларда дисперстік жүйелерге қолданылмау себебі коллоидтық бөлшектердің арасындағы тартылу күштерінің байқалуында. Бұл жағдайда жүйеде дисперсиялық ортаның байқалатын көлемін қосатын босаңқы құрылымдар түзіледі. Мұндай иммобилизация, яғни еріткіштің қозғалғыш-тығының азаюы, жүйенің тұтқырлығын Эйнштейн теңдеуінен шыққаннан едәуір үлкен болуына әкеледі. Мұндай жүйелердегі тұтқырлық ағу жылдамдығына қатты тәуелді, себебі жүйеде босаң кеңістіктік торлардың болуымен шартталатын құрылымдық тұтқырлық болып келеді. Басқа жағынан қарағанда, коллоидтық жүйелерге Эйнштейн теңдеуінің қолданылмайтындығы аттас зарядтары бар бөлшектердің арасында тебілу күштерінің де байқалуымен де байланысты. Смолуховскийге сәйкес зарядталған бөлшектері бар кірнелердің зарядталмағандарға қарағанда тұтқырлығы жоғары. Бөлшектердің бетінде қос электрлік қабаттың болуы нәтижесінде тұтқырлықтың өсуі электртұтқырлықтық эффект деп аталады. Смолуховский кірненің меншікті тұтқырлығын қос электрлік қабаттың электрокинетикалық ξ-потенциалымен байланыстыратын теңдеуді шығарды:
мұнда η0-дисперсиялық ортаның тұтқырлығы, γ-меншікті электрөткізгіштік, r-бөлшектердің радиусы, ε-диэлектрлік өтімділік. (2.22) теңдеуідегі түзетпе мүшесінің бөлшегінің үлкен маңызы бар. Есептеулердің көрсетуі бойынша радиусы 10-6см, электрөткізгіштігі γ=10-4Ом-1см-1 бөлшектері бар кірнелер үшін түзетпе мүшесі негізгіден 10 есе артық болуы мүмкін. Смолуховский теңдеуіне сәйкес коллоидтық жүйелердің тұтқырлығы электроллиттерді енгізгенде ξ- потенциалдың төмендеуі салдарынан да, мицеллааралық сұйықтықтың электрөткізгіштігінің артуы нәтижесінде де азаюы керек. Кірненің изоэлектрлік күйінде (ξ=0) Смолуховский теңдеуі Эйнштейн теңдеуіне айналады. Алайда коллоидтық жүйеге электролит енгізгендегі астабилизациясы кезінде (кірненің бөлшектері арасындағы тебілу күштерінің төмендеуі салдарынан) Смолуховский теңдеуімен көрсетілмеген құрылымдар түзілу мен құрылымдық тұтқырлықтың пайда болуына әкелетін бөлшектердің агрегациясы болуы мүмкін. Осының нәтижесінде кірне бөлшектерінің ξ-потенциалының төмендеуі белгілі жағдайларда кірненің тұтқырлығын төмендетпей, оның көбеюіне жағдай жасауы мүмкін. Смолуховский теңдеуіне бөлшектердің радиусы кіретіндіктен, бөлшектері электр зарядын таситын кірнелердің тұтқырлығы зарядталмаған бөлшектері бар зольдердің тұтқырлығынан қарағанда дисперстілік дәрежесіне тәуелді болады. 1948ж. Буутс электртұтқырлық эффектісі үшін Смолуховский теңдеуінен ерекше теңдеуді қорытып шығарды. Буутсқа сәйкес Смолуховский теңдеуіне қарағанда электртұтқырлық эффектісінің шамасы едәуір төмен және бөлшектің радиусымен салыстырғанда қос электрлік қабаттың қалыңдығы өте аз болғанда, ξ-потенциалдың мәніне тәуелсіз өте мардымсыз болады.
XVIII тарау Қоршаған ортаны қорғаудың коллоидтық химиялық негіздері Қоршаған ортаны қорғау қазіргі кездегі адамзаттың ең негізгі мәселелерінің бірі. Соңғы жылдары бұл басты мәселеге айналды. Бұл мәселемен барлық мамандар айналасуда. Бұл тарауда, әринеә мәселенің аспектілерінің көбі, мысалы, қорықтарды қаршау, экологиялық заң құруының сұрақтары және т.б. қарастырылмайды. Мәселені химия тұрғысында қарастыру коллоидтық химияның химиялық пәндердің арасында басты роль атқаратынын көрсетті. Мысалы, әртүрлі молекулалар, иондар және коллоидтық бөлшектер түріндегі ластануды ауа немесе сулы ортадан аластату. Молекулалар мен иондарды тазарту әдістерінің барлығы делік коллоидтық химиялық нысандар мен әдістерге негізделген. Әртүрлі жұтқыштар, жарғақтар, сүзгіштер және т.б. дисперстік жуйелер болып табылады және адамзат олардағы беттік құбылыстарды ауа мен судағы барлық ластануларды жою үшін қолданылады. Су мен атмосфераны тазалау кәдімгі коллоидтық үдерістер. Міне, сондықтан да қоршаған ортаны қорғауда коллоидтық химиялық негіздері туралы айтуға болады. Бұл саланың бірқатар мәселелері төңірегіндегі курстың басқа бөлімдерінде айтарлықтай терең қарастырылған. Атап айтқанда, әртүрлі дене бетіндегі газдар мен ерітінділерден молекулалардың адсорбциясы, ерітінділердегі ион алмасу және электрдиализ және т.б. арқылы иондарды аластату. Бұл тарауда коллоидтық химиялық заңдылықтардың бізді қоршаға табиғи ортаны қорғау әдістерін әзірлеуде қолданылатыны, дәлірек айтқанда, суды тазалау, аэрокірнелер атмосферадан арылту әдістері қарастырылады. |
|

 алса, онда φ үшін:
алса, онда φ үшін: (2.20)
(2.20) (2.21)
(2.21) шамасы кемиді, бұл концентрацияға қарағанда тұтқырлықтың тезірек өсуіне әкеледі.
шамасы кемиді, бұл концентрацияға қарағанда тұтқырлықтың тезірек өсуіне әкеледі. (2.22)
(2.22)