|
|
Формы представления чисел в ЭВМВ ЭВМ применяется две формы представления чисел: 1 Естественная форма или форма с фиксированной точкой. 2 Нормальная форма или форма с плавающей точкой. Фиксированная точка В современных компьютерах естественная форма используется только для целых чисел. В памяти ПК числа с фиксированной точкой хранятся в трех форматах: а) полуслово – 2 байта; б) слово – 4 байта; в) двойное слово – 8 байт. Целые числа могут быть представлены как с учетом их знака, т.е. алгебраические числа, так и без знака. Для алгебраического числа знак кодируется двоичной цифрой и размещается в старшем разряде числа. При этом код “0” означает знак “+”, а код “1” - знак “-“. Для алгебраического представления чисел в ЭВМ используются специальные коды: а) прямой код числа; б) обратный код; в) дополнительный код. При этом два последних кода позволяют заменить неудобную для компьютера операцию вычитания на операцию сложения с отрицательным числом. Дополнительный код обеспечивает более быстрое выполнение операций. Поэтому в ЭВМ чаще всего применяется именно он. Прямой код числа N (обозначим [N]пр). Пусть N = a1, a2, a3, …, am, тогда: при N > 0, [N]пр = 0, a1, a2, a3, …, am; при N < 0, [N]пр = 1, a1, a2, a3, …, am; при N = 0 имеет место неоднозначность [0]пр = 0, 00…0= 1, 00…0. Прямой код используется только для ввода чисел в ЭВМ. Обратный код числа N (обозначим [N]обр). Пусть N = a1, a2, a3, …, am, и при N > 0, [N]обр = 0, a1, a2, a3, …, am; при N < 0, [N]обр = 1, при N = 0 имеет место неоднозначность [0]обр = 0, 00…0= 1, 11…1. Для того, чтобы получить обратный код отрицательного числа, необходимо все цифры этого числа проинвертировать. Например: N = 1011 [N]обр = 0,1011 N = -1011 [N]обр = 1,0100 Дополнительный код числа N (обозначим [N]доп). Пусть как и раньше N = a1, a2, a3, …, am, и при N ≥ 0, [N]доп = 0, a1, a2, a3, …, am; при N ≤ 0, [N]доп = 1, Для того, чтобы получить дополнительный код отрицательного числа, необходимо сначала получить обратный код этого числа, а затем к младшему разряду прибавить единицу. Например: N = 1011 [N]доп = 0,1011 N = -1011 [N]доп = 1,0101 N = +0000 [N]доп = 0,0000 N = -0000 [N]доп = 1,1111 +0,0001 10,0000 Так как единица переноса из знакового разряда исчезает, то неоднозначности в изображении нуля нет. Эмпирическое правило: для получения дополнительного кода отрицательного числа необходимо все символы этого числа инвертировать, кроме последней единицы и тех нулей, которые за ней стоят. Плавающая точка В форме представления с плавающей точкой число изображается в виде двух групп цифр. Первая группа цифр называется мантиссой, вторая – порядком. Число представляется в виде произведения X = ±mq±P, где m – мантисса числа Х, P – порядок числа, q – основание системы счисления. Для представления числа в форме с плавающей точкой в двоичной СС, т.е. при q = 2, требуется задать знаки мантиссы и порядка и их модули: Модуль порядка Модуль мантиссы
В современных ЭВМ для упрощения операций над порядком последний приводят к целым положительным числам, применяя так называемый смещенный порядок. Для этого к истинному порядку добавляется целое положительное число, называемое смещением. Смещенный порядок Модуль мантиссы
Обычно смещение выбирается равным половине представимого диапазона порядка. В ПК для представления чисел с плавающей точкой используется два формата: - 32-х битовый формат; - 64-х битовый формат. При 32-х битовом формате под порядок выделяется 8 разрядов. Так как 28 = 256, то смещение будет равно 128. Тогда, если, например, порядок числа равен (-3), то в ЭВМ он будет представлен как 128 – 3 = 125. Типичный 32-х битовый формат числа с плавающей точкой для ПК имеет вид: 0 1 8 9 31
Мантисса числа с плавающей точкой обычно представляется в нормализованной форме. Это означает, что на мантиссу налагаются такие условия, чтобы она по модулю была меньше единицы, т.е. (IqI < 1), а первая цифра после точки отличалась от нуля. Если первые i цифр мантиссы равны нулю, то для нормализации её нужно сдвинуть относительно точки на i разрядов влево с одновременным уменьшением порядка на i единиц. В результате такой операции число не изменяется. Однако при первичном представлении числа нормализация обеспечивает повышение точности представления этого числа. Для повышения точности представления мантиссы применяют еще один способ, называемый приемом скрытой единицы. Суть его в том, что в нормализованной мантиссе старшая цифра всегда равна 1. Следовательно, эту цифру можно не записывать, а подразумевать. Запись мантиссы начинается с ее второй цифры. Это позволяет задействовать дополнительный значащий бит для более точного представления числа. Следует иметь в виду, что значение порядка при этом не меняется. Скрытая единица перед выполнением арифметических операций восстанавливается, а при записи результата – удаляется. Для более существенного увеличения точности вычислений под число отводят несколько машинных слов. В ПК для этого и применяется 64-х битовый формат: 1 бит 11 битов 52 бита
Диапазоны представления чисел в ПК: - при 32-х битовом формате: 10-38 до 10+38; - при 64-х битовом формате: 10-308 до 10+308 Для сравнения: количество секунд, которые прошли с момента образования планет Солнечной системы, составляет около 1018. Логические основы ЭВМ Математической базой для построения электронных схем ЭВМ является алгебра логики, разработанная Джорджем Булем в середине ХIХ века. Алгебра логики оперирует с высказываниями. Под высказыванием понимают повествовательное предложение, относительно которого можно утверждать, истинно оно или ложно. Например, выражение «Расстояние от Москвы до Томска больше, чем от Москвы до Новороссийска» истинно, а выражение «5<2» - ложно. Высказывания принято обозначать буквами латинского алфавита: A, B, C, …, X, Y и т.д. Если высказывание С истинно, то пишут С = 1, а если оно ложно, то С= 0. В алгебре логики над высказываниями можно производить определенные логические операции, в результате которых получаются новые высказывания. Истинность полученных высказываний зависит от истинности исходных высказываний и использованных для их преобразования логических операций. Из всего набора логических операций в ЭВМ применяются только четыре: 1 Конъюнкция. 2 Дизъюнкция 3 Инверсия 4 Сумма по модулю два. Рассмотрим логические операции и соответствующие им элементы логических схем. Конъюнкция. Соединение двух (или нескольких) высказываний в одно с помощью союза И (AND) называется операцией логического умножения, или конъюнкцией. В логических выражениях эту операцию принято обозначать знаком «^» или знаком умножения «*», а на электронных схемах –знаком «&». Сложное высказывание А & В истинно только в том случае, когда истинны оба входящих в него высказывания. Истинность такого высказывания задается табл.
Логическая схема И реализует конъюнкцию двух или более логических значений. Условное обозначение схемы И с двумя входами представлено на рис.
Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет нуль, на выходе также будет нуль. Связь между выходом z этой схемы и входами х и у описывается соотношением: z = x & у (читается как «х И у»). Дизъюнкция. Объединение двух (или нескольких) высказываний с помощью союза ИЛИ (OR) называется операцией логического сложения, или дизъюнкцией. В логических выражениях эту операцию принято обозначать знаком «v» или знаком сложения «+»,а на электронных схемах – знаком «1». Сложное высказывание A v В истинно, если истинно хотя бы одно из входящих в него высказываний. Истинность такого высказывания задается табл.
Схема ИЛИ реализует дизъюнкцию двух или более логических значений. Условное обозначение схемы ИЛИ с двумя входами представлено на рис.
Когда хотя бы на одном входе схемы ИЛИ будет единица, на ее выходе также будет единица. Связь между выходом z этой схемы и входами х и у описывается соотношением: z = x v у (читается как «х ИЛИ у»). Инверсия. Присоединение частицы НЕ (NOT) к некоторому высказыванию называется операцией отрицания (инверсии) и обозначается
Схема НЕ (инвертор) реализует операцию отрицания. Условное обозначение схемы инвертора имеет вид:
Если на входе схемы «0», то на выходе «1», и наоборот. Связь между входом х этой схемы и выходом z можно записать соотношением z = Сумма по модулю два (иначе называется ИСКЛЮЧАЮЩЕЕ ИЛИ). Результатом выполнения операции сложения по модулю два является только остаток от сложения, т.е. перенос в старший разряд отбрасывается. В логических выражениях эту операцию принято обозначать знаком «
Схема ИСКЛЮЧАЮЩЕЕ ИЛИ соответствует сложению по модулю два двух логических значений. Условное обозначение схемы ИСКЛЮЧАЮЩЕЕ ИЛИ представлено на рис.
Когда только на одном входе схемы ИСКЛЮЧАЮЩЕЕ ИЛИ будет единица, на ее выходе также будет единица. Связь между выходом z этой схемы и входами х и у описывается соотношением: z = x Кроме схемных элементов, соответствующих перечисленным логическим операторам, в состав логических схем входят комбинированные связки, именуемые вентилями, например следующие. Схема И—НЕ состоит из элемента И и инвертора и осуществляет отрицание результата схемы И. Таблица истинности схемы И—НЕ имеет вид:
Связь между выходом z и входами х и у схемы записывают как z =
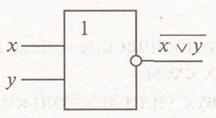
Схема ИЛИ—НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ. Таблица истинности схемы ИЛИ—НЕ имеет вид:
Связь между выходом z и входами х и у схемы записывают как z =
Все рассмотренные схемы, реализующие логические операции над двоичными переменными, называются комбинационными логическими элементами. Число входов комбинационного логического элемента соответствует числу аргументов воспроизводимых им одной или нескольких булевых функций. Подобно тому как сложная булева функция может быть получена суперпозицией более простых функций, так и путем объединения комбинационных логических элементов, т.е. соединением их входов и выходов, можно получить сложную схему, которую называют комбинационной схемой В комбинационных схемах совокупность выходных сигналов (выходное слово Y) в любой момент времени однозначно определяется входными сигналами (входным словом Х), поступающими на входы в тот же момент времени. Функциональное обозначение комбинационной схемы имеет вид:
Реализуемый в этих схемах способ обработки данных называется комбинационным, т.к. результат обработки зависит только от комбинации входных сигналов и вырабатывается сразу при подаче входных данных. Закон функционирования КС определен, если задано соответствие между ее входными и выходными словами, например, в виде таблицы истинности. Это соответствие может быть задано и в аналитической форме с использованием булевых функций.
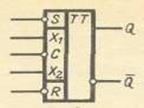
Лекция 5 Запоминающие элементы ЭВМ Триггеры Триггер является элементом, который может находиться в одном из двух устойчивых состояний. Одному из этих состояний приписывается значение 1, а другому —0. Состояние триггера распознается по его выходному сигналу. Под влиянием входного сигнала триггер скачкообразно переходит из одного устойчивого состояния в другое, при этом скачкообразно изменяется уровень напряжения его выходного сигнала. Для удобства использования в схемах вычислительных устройств триггеры обычно имеют два выхода: прямой Q (называется также «выход 1») и инверсный Q («выход 0»). В единичном состоянии триггера на выходе Q высокий уровень сигнала, а в нулевом — низкий. На выходе Q наоборот. Схемы триггеров можно разделить на несколько типов: с установочными входами — RS-триггер, со счетным входом — Т-триггер, а также D-триггер, JK-триггер и др. Если хотя бы с одного входа информация в триггер заносится принудительно под воздействием синхронизирующего сигнала, то триггер называется синхронизируемым (синхронным). Если занесение информации в триггер с любого входа производится без синхронизирующего сигнала, то триггер называется несинхронизируемым (асинхронным). Общая форма условного обозначения триггеров показана на рис.
В основном поле ставится символ Т или символ ТT для обозначения соответственно однотактного или двухтактного триггера. Дополнительное поле может быть разделено на две части: асинхронную и синхронную. В первой проставляются символы R и S входов несинхронизируемой установки триггера в 1 и 0, во второй — на местах X1 и Х2 символы в соответствии с типом триггера. При этом пользуются следующими обозначениями для входов: S — вход установки триггера в 1; R — вход установки триггера в 0; Т — вход триггера со счетным входом; D — вход D-триггера; С — вход синхронизации. Если вход отмечен кружком, это означает, что действующее значение входного сигнала —0. Например, отсутствие кружка на входе С на рис. указывает на то, что входная информация заносится в триггер при единичном значении синхронизирующего сигнала (действующее значение синхронизирующего сигнала равно 1); кружок на входе С означает, что прием информации происходит при нулевом значении синхронизирующего сигнала (действующее значение синхронизирующего сигнала равно 0). Состояние триггера определяется сигналом Q на прямом выходе триггера. Законы функционирования триггеров задаются таблицами переходов с компактной записью, при которой в столбце состояний может быть указано, что новое состояние совпадает с предыдущим либо является его отрицанием. Асинхронный RS-триггер. Асинхронный (несинхронизируемый) RS-триггер на интегральных элементах ИЛИ — НЕ показан на рис.
Функциональная схема RS-триггера Триггер образован из двух комбинационных схем ИЛИ — НЕ, соединенных таким образом, что возникают положительные обратные связи, благодаря которым в устойчивом состоянии выходной транзистор одной схемы ИЛИ — НЕ закрыт, а у другой открыт. Таблица переходов, определяет закон функционирования этого триггера.
При R =1 и S = 0 триггер устанавливается в нулевое состояние Q = 0; при R= 0 и S = l он устанавливается в единичное состояние Q = 1; при R = S = 0 триггер сохраняет состояние, в котором он находился до момента поступления на его входы нулевых сигналов. При R = S = 1 на прямом и инверсном выходах устанавливается нулевой сигнал. Триггерное кольцо превращается в два независимых инвертора, и при переходе к хранению (R = S = 0) триггер может устанавливаться в любое состояние. Поэтому такая комбинация входных сигналов запрещена.
Условное обозначение асинхронного RS-триггера имеет вид:
Синхронизируемый однотактный RS-триггер. Схема синхронизируемого
однотактного RS-триггера на элементах И - НЕ имеет вид: Функциональная схема синхронизируемого однотактного RS-триггера Здесь элементы 1 и 2 образуют схему входной логики асинхронного RS-триггера, построенного на элементах 3 и 4. Такие RS-триггеры имеют два информационных входа R и S и вход синхронизации С. Кроме того, триггер может иметь несинхронизируемые входы R и S. В этом случае функционирование триггера осуществляется либо под воздействием несинхронизируемых входов при С=0, либо под воздействием синхронизируемых входов. В последнем случае на несинхронизируемых входах должны присутствовать сигналы, которые не влияют на состояние схемы. Работа триггера осуществляется в соответствии с таблицей при сигнале несинхронизируемого входа
Входная информация, представленная в парафазном коде, заносится в синхронизируемый однотактный RS-триггер через элементы входной логики 1 и 2 в момент поступления сигнала синхронизации С. В отсутствие сигнала синхронизации триггер может быть установлен в состояние 0 путем подачи на несинхронизируемый вход Rсигнала 0. Условное обозначение синхронного RS-триггера имеет вид:
Лекция 6 Представление данных физическими сигналами
В предыдущих лекциях мы установили, что данные любого исходного вида в ЭВМ представляется в двоичном алфавите. Физическими аналогами знаков 0 и 1 двоичного алфавита служат сигналы, способные принимать два хорошо различимых значения, например, напряжение (потенциал) высокого и низкого уровней, отсутствие и наличие электрического импульса, противоположные по знаку значения магнитной индукции и т. п. В схемах цифровых устройств переменные и соответствующие им сигналы изменяются не непрерывно, а лишь в дискретные моменты времени, обозначаемые целыми неотрицательными числами: 0, 1, 2, ..., i ... Временной интервал между двумя соседними моментами дискретного времени называется тактом. Во многих случаях цифровые устройства содержат специальный блок, вырабатывающий синхронизирующие сигналы (СС), отмечающие моменты дискретного времени (границы тактов). В цифровых вычислительных устройствах обычно применяют потенциальный и импульсный способы физического представления информации. При потенциальном способе двум значениям переменной 1 и 0 соответствуют разные уровни напряжения в соответствующей точке схемы машины (потенциальный код). Потенциальный сигнал сохраняет постоянный уровень в течение такта, а его значение в переходные моменты не является определенным. При импульсном способе представления информации единичное и нулевое значения двоичной переменной отображаются наличием и отсутствием электрического импульса в соответствующей точке схемы (импульсный код).
Импульсный сигнал можно характеризовать амплитудой Um, продолжительностью импульса по основанию tосн, длительностью фронта tфр и среза tср. Аналогичные понятия могут быть применены к потенциальному сигналу. Потенциальный сигнал характеризуется, кроме того, разностью Uсверхнего и нижнего уровней напряжения. Понятия фронта и среза у потенциального сигнала всегда связаны с процессом перехода соответственно от нижнего к верхнему и от верхнего к нижнему уровню напряжений. В соответствии с типом используемых сигналов для представления данных схемы цифровых устройств принято делить на импульсные, потенциальные и импульсно-потенциальные. Слово может быть представлено последовательным или параллельным кодом. При последовательном коде каждый временной такт предназначен для отображения одного разряда кода слова. В этом случае все разряды слова фиксируются по очереди одним и тем же элементом и проходят через одну линию передачи информации.
Последовательный импульсный код (а) и последовательный потенциальный код (б) При параллельном коде все разряды двоичного кода слова представляются в одном временном такте, фиксируются отдельными элементами и проходят через отдельные линии, каждая из которых служит для представления и передачи только одного разряда слова.
Параллельный импульсный код (а) и параллельный потенциальный код (б) При параллельной передаче информации код слова развертывается не во времени, а в пространстве, так как значения всех разрядов слова передаются по нескольким линиям одновременно. В зависимости от применяемого кода устройства вычислительной техники называются последовательными или параллельными. При использовании последовательного кода все операции, в том числе передача слов из одного узла в другой, производятся поочередно для каждого разряда слова, и поэтому последовательные устройства работают медленнее, чем параллельные. В современных ЭВМ основные устройства, участвующие в обработке информации, для достижения высокого быстродействия строятся как параллельные, хотя они и требуют большего объема аппаратуры. Для экономии оборудования в некоторых устройствах применяют последовательно-параллельный код, при котором слова разбиваются на части (слоги) и передача, а иногда и обработка производятся последовательно слог за слогом. При этом каждый слог представляется параллельным кодом. Цифровые автоматы Преобразование информации в ЭВМ производится электронными устройствами (логическими схемами) двух классов: комбинационными схемами и цифровыми автоматами. Комбинационные схемы были рассмотрены на предыдущей лекции. Другой, более сложный класс преобразователей дискретной информации составляют цифровые автоматы. Цифровой автомат в отличие от комбинационной схемы имеет некоторое конечное число различных внутренних состояний. Под воздействием входного слова цифровой автомат переходит из одного состояния в другое и выдает выходное слово. Выходное слово на выходе цифрового автомата в такте определяется в общем случае входным словом, поступившим в этот такт на вход автомата, и внутренним состоянием автомата, которое явилось результатом воздействия на автомат входных слов в предыдущие такты. Комбинация входного слова и текущего состояния автомата в данном такте определяет не только выходное слово, но и то состояние, в которое автомат перейдет к началу следующего такта. Структура цифрового автомата имеет вид:
Цифровой автомат содержит память, состоящую из запоминающих элементов (ЗЭ) — триггеров, элементов задержки и др., фиксирующих состояние, в котором он находится. Комбинационная схема не содержит ЗЭ. Поэтому ее называют автоматом без памяти или примитивным автоматом. Структурная схема цифрового автомата содержит запоминающие элементы ЗЭ1— 3Эк и комбинационные схемы КСI и КСII. Состояния ЗЭ, определяющие состояние автомата, передаются в форме сигналов qj по цепям прямой связи на входы КСII и по цепям обратной связи на входы КСI. На входы комбинационных схем поступают также сигналы x1, ...,xn с входов автомата. Выходное слово вырабатывается в КCII,, причем входными переменными для нее служат буквы входного слова и состояния ЗЭ — состояние автомата. Выходные сигналы КСI переводят автомат (его ЗЭ) в новое состояние, при этом входными переменными для этой схемы служат буквы входного слова и состояния ЗЭ. Одновременность появления новых значений входных сигналов на всех входах устройства достигается с помощью тактирующих сигналов, называемых также синхросигналами, обеспечивающих передачу информации с ЗЭ на входы комбинационной схемы одновременно с сигналами, поступающими на ее входы с других устройств. Способы передачи данных Особенности построения цифровых устройств связаны со способом передачи данных между логическими элементами. Передача данных от элемента к элементу может осуществляться не синхронизируемым (асинхронным) и синхронизируемым способами, причем последний используется только при передаче данных в запоминающие элементы. При асинхронном способе передачи данных входные сигналы логических элементов преобразуются с небольшой задержкой в выходные сигналы, которые непосредственно воздействуют на входы следующих логических элементов. При синхронизируемом способе передачи данных входные сигналы воздействуют на запоминающие логические элементы в строго определенные моменты времени, соответствующие появлению синхронизирующих сигналов. Передача данных между запоминающими логическими элементами в общем случае требует выполнения следующего условия: она производится только после завершения передачи данных о предыдущем состоянии принимающего данные элемента другому ЗЭ. Для выполнения этого условия в потенциальных схемах используется несколько серий синхронизирующих сигналов, сдвинутых во времени относительно друг друга так, что когда сигнал одной серии принимает значение 1, то сигнал другой серии — значение 0.
Лекция 7 Архитектура ЭВМ |
|
 обозначает инверсию а, т.е. если а = 1, то
обозначает инверсию а, т.е. если а = 1, то 

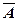 .Если высказывание А истинно, то
.Если высказывание А истинно, то 
 , где
, где 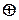 »,а на электронных схемах – знаком «=1». Сложное высказывание A
»,а на электронных схемах – знаком «=1». Сложное высказывание A 
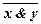







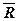 = 1 и при С=1.
= 1 и при С=1.



