|
|
Времени падения тела с заданной высотыПромахи Промахи, как правило, вызываются невнимательностью (например, при измерении диаметра отверстия штангенциркулем часто забывают учесть толщину его ножек). Они могут возникать также вследствие неисправности прибора. От промахов не застрахован никто, однако по мере приобретения экспериментальных навыков вероятность промахов заметно уменьшается. Систематические погрешности Систематические погрешности могут возникать по ряду причин, вот некоторые из них. 1. Несоответствие прибора эталону (например, пластмассовые линейки с течением времени обычно укорачиваются на несколько миллиметров, секундомер может иметь неправильный ход - спешить или отставать на несколько секунд в сутки). 2. Неправильное использование прибора (например, перед взвешиванием не установлено равновесие ненагруженных весов). 3. Пренебрежение поправками, которые нужно ввести в результаты измерения для достижения требуемой точности (например, не учтена зависимость температуры кипения воды от атмосферного давления). Систематические погрешности, обусловленные некоторыми из этих причин, могут быть сведены к минимуму проверкой приборов, их тщательной установкой, анализом необходимых поправок и т.д. Погрешности, вызванные некоторыми причинами могут быть скрыты в течение длительного времени и обычно обнаруживаются при нахождении тех же физических величин принципиально другими методами. Анализ подобного рода систематических погрешностей может в ряде случаев привести к открытию неизвестных ранее явлений природы. В учебных лабораториях систематические погрешности обычно игно- рируются и анализ их не производится. Случайные погрешности Случайные погрешности вызываются большим числом неконтролируемых причин, влияющих на процесс измерения. Такие причины могут быть объективными (неровности на поверхности измеряемого предмета; дуновение воздуха, ведущее к изменению температуры; скачкообразное изменение напряжения электрической сети и т.п.) и субъективными (разная сила зажима предмета между ножками штангенциркуля, неодинаковое расположение глаза по отношению к шкале прибора, различное запаздывание при включении секундомера и т.п.). Эти причины могут сочетаться в различных комбинациях, вызывая то увеличение, то уменьшение значения измеряемой величины. Поэтому при измерениях одной и той же величины несколько раз получается, как правило, целый ряд значений этой величины, отличающихся от истинного значения случайным образом. Закономерности, описывающие поведение случайных величин, изучаются теорией вероятностей. Под вероятностьюмы здесь будем подразумевать отношение числа случаев, удовлетворяющих какому-либо условию, к общему числу случае, если общее число случаев очень велико (стремится к бесконечности). Максимальное значение вероятности равно единице (все случаи удовлетворяют заданному условию). При описании случайных погрешностей обычно используются следующие предположения. 1. Погрешности могут принимать непрерывный ряд значений. 2. Большие отклонения измеренных значений от истинного значения измеряемой величины встречаются реже (менее вероятны), чем малые. 3. Отклонения в обе стороны от истинного значения равновероятны. Эти предположения справедливы не всегда. Опыт, однако, показывает, что все же в подавляющем большинстве случаев они выполняются достаточно хорошо.
Связь между случайными (DХсл) и приборными (DХпр) погрешностями установлена в математической статистике и проиллюстрирована (рис.4). Как следует из этого рисунка, полная погрешность будет равна:
Если Наоборот, если
5. ЭЛЕМЕНТЫ ТЕОРИИ СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ
Вероятность попадания случайной величины в интервал от -∞ до +∞ всегда равна единице:
т.е. такое событие будет достоверным – измеряемую величину всегда можно обнаружить в интервале значений
 , т.е. , т.е.  является наилучшим приближением к истинному значению. является наилучшим приближением к истинному значению.
Графически функция распределения f(X), подчиняющаяся НЗР, представлена на рис.5 где σ – средняя квадратичная погрешность, определяемая по формуле:
Причем средняя квадратичная погрешность (12) подбирается так, что при проведении серии измерений из большого числа опытов в 67% случаев абсолютная погрешность ∆X < σ, а в остальных (33%) случаях ∆Χ > σ. На рис.5 заштрихованная площадь составляет около 67% от всей площади под кривой, т.е. наиболее часто встречаются случайные величины Xi в интервале от (Xв,-σ) до (Xв,+σ) и гораздо реже – за пределами этого интервала (справа и слева). Как показал анализ, для функции распределения f(X), подчиняющейся НЗР (рис.5), характерны следующие свойства: а) кривая функции распределения f(X) симметрична относительно прямой X = Xв , т.е. отклонения случайных величин от Хв вправо и влево равновероятны и встречаются одинаково часто; Хв – наиболее вероятное значение случайной величины; б) при Х = Хв плотность вероятности принимает максимальное значение fmax(X); в) наиболее вероятное значение Хв совпадает со средним арифметическим значением г) при Х→0 и Х→∞ кривая функции распределения асимптотически приближается к оси абсцисс (f(X)→0). 5.3 Вероятность того, что истинное значение содержится в интервале Погрешность, определяемая с надежностью α = 0,67, называется стандартной погрешностью (σст). Таким образом, для характеристики случайной погрешности следует учитывать не только саму величину, но и доверительный интервал, определяемый с надежностью α. Поэтому результат физического эксперимента записывают в виде: 5.4 Как уже указывалось, средняя квадратичная погрешность σст, определяемая формулой (12), подбирается так, что вероятность того, что результат измерения отличается от истинного не более, чем на σст, равна α=0,67. В этом случае, отношение В табл.3 приведены значения доверительной надежности α при различных значениях отношения β. Из таблицы видно: вероятность того, что измеренная величина отличается от истинного на величину Таблица 3
Анализ табл.3 показывает, что при α = 0,67 коэффициент β =1 и абсолютная погрешность ∆Χ = На практике условились считать погрешности грубыми, если 5.5 Данные, приведенные в табл.3, получены при большом числе опытов (n > 30). Для оценки доверительной вероятности α в случае малого числа опытов (n
Для заданного числа опытов (n = const) и заданной надежности ( Поэтому выбор высокой надежности не всегда оправдан. На практике, чаще всего, надежность выбирают не более чем 0,95 (α 5.6 Выразим абсолютную погрешность ∆Χ из формулы (14)
Подставив в эту формулу значение σст из (12), получим формулу для расчета случайной погрешности в общем виде:
Оценив
6. МЕТОДИКА ОБРАБОТКИ СЛУЧАЙНЫХ ВЕЛИЧИН. ГИСТОГРАММА
6.1 Пусть в результате эксперимента по измерению случайной величины получен статистический ряд значений: X1, X2, …,Xn. Для наглядного представления распределения случайных величин Xi полученный ряд значений записывают в упорядоченном виде по мере возрастания от Xmin до Xmax (или, наоборот, по мере убывания от Xminдо Xmax). Далее разбивают упорядоченный ряд на некоторое число К интервалов одинаковой ширины
 (17) (17)
Подсчитав число m элементов ряда, попавших в каждый из полученных интервалов. Затем представляют распределение случайных величин графически, откладывая по оси абсцисс случайные величины из упорядоченного ряда с интервалом ∆Χ0, а по оси ординат число m попаданий элементов в каждый из полученных интервалов (рис.6). Построив прямоугольники со сторонами ∆Χ0 (ширина) и m (высота), получают ступенчатую «кривую», которая называется гистограммой.
 (рис.6, заштрихованная площадь). С увеличением числа опытов (n→∞) и числа интервалов (К→∞), на которое разбивается статистический ряд случайных величин, в пределе (рис.6, заштрихованная площадь). С увеличением числа опытов (n→∞) и числа интервалов (К→∞), на которое разбивается статистический ряд случайных величин, в пределе  , и гистограмма вырождается в плавную кривую (рис.7, сплошная линия). При этом наиболее вероятное значение Xв совпадает со средним арифметическим значением , и гистограмма вырождается в плавную кривую (рис.7, сплошная линия). При этом наиболее вероятное значение Xв совпадает со средним арифметическим значением  . Это является одним из признаков, позволяющих считать распределение случайных величин в соответствии с НЗР Гаусса. . Это является одним из признаков, позволяющих считать распределение случайных величин в соответствии с НЗР Гаусса.
7. ПРАВИЛА ОБРАБОТКИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ В ФИЗИЧЕСКОМ ЭКСПЕРИМЕНТЕ
7.1 При обработке результатов измерений в физическом эксперименте рекомендуется придерживаться следующих правил округления чисел.
Например, если получено значение ∆Χ = 0,238, то после округления получим ∆Χ ≈ 0,3. Другой пример: ∆Χ = 0,0127. После округления получим ∆Χ ≈ 0,013.
Например, при измерении скорости пули были получены результаты: 7.2 Запись результатов в виде (18) означает, что истинное значение а измеряемой величины лежит в интервале от ( Кроме того, запись вида (18) позволяет судить о том, в каком разряде числа содержится неточность (сомнительная цифра), и какие цифры являются верными. 7.3 Алгоритм обработки прямых измерений представлен в табл.4. Таблица 4
7.4 Формулы, связывающие исследуемую величину с измеряемыми, часто содержат постоянные величины (например, g – ускорение свободного падения, R – универсальная газовая постоянная, число π и т.д.). Все физические константы являются приближенными. За абсолютную погрешность физической константы принимается половина последнего разряда числа. Например, если принять g = 9,8 7.5 В случае косвенных измерений обработку результатов эксперимента можно производить двумя способами. а) Если исследуемая величина определяется несколько раз при неизменных внешних условиях, то расчет погрешностей можно проводить выше описанным методом – по формуле Стьюдента (табл. 4). Например, при определении периода колебаний T математического маятника заданной длинны (
для каждого опыта; а затем находят значение ‹T›. Дальше обработку результатов измерений проводят в соответствии с табл.4. б) Если же внешние условия меняются в ходе эксперимента (например, изменяется длина маятника На практике часто применяют следующий способ получения формулы относительной погрешности (табл.5).
Таблица 5
7.6 Рассмотрим пример обработки косвенных измерений периода колебаний математического маятника (табл.6.) при неизменных внешних условиях: Таблица 6
Рассчитаем случайную абсолютную погрешность по формуле Стьюдента (16).
где tα,n = t0,95;3 = 4,3 (табл.50, прил.IV) Учитывая расчеты, приведенные в табл.6, найдем значение абсолютной погрешности определения периода колебаний.
После округления (до первой значащей цифры с избытком), получим ∆T ≈ 0,004 c. Затем, округлив среднее значение до разряда тысячных долей, запишем результат в виде: T = (2,014 + 0,004) c. (с надежностью α = 0,95). Рассчитаем относительную погрешность:
Рассмотрим теперь пример обработки результатов косвенных измерений, когда длина маятника в процессе эксперимента изменяется (табл.7). Таблица 7
 ). ).
Для выяснения характера этой зависимости построим график в координатах «T -
Поэтому при обработке результатов измерений среднее значение определить нельзя и погрешность следует оценивать согласно методике, изложенной в п.7.4. Следуя предложенному алгоритму (табл.5), прологарифмируем выражение (20):
Затем полученное выражение дифференцируем. Получаем соотношение:
Заменив значок дифференциала «d» на значок конечного приращения «∆» и знаки «-» на «+», получим формулу:
Формула максимальной относительной погрешности будет иметь вид:
где ∆π = 0,005 (п. 7.3); ∆g = 0,05 м/с2 (если g = 9,8 м/с2) и ∆ Рассчитаем относительную погрешность εi для каждого опыта (табл.8).
Сравнивая погрешности между собой, видим, все три погрешности совпадают с точностью до тысячных долей, т.е. ε1 ≈ ε2 ≈ ε3 ≈ 0,026. Поэтому нет смысла рассчитывать εi для каждого опыта, а достаточно определить ε для одного из опытов (обычно, из средней части таблицы экспериментальных данных). Абсолютные погрешности численно могут отличаться друг от друга, но по порядку числа они получаются одинаковыми. В нашем примере:
Результаты измерений запишем в виде: T1 = (1,55 ± 0,05) с; T2 = (1,79 ± 0,05) с; Т3 = (2,00 ± 0,06) с. Таким образом, при обработке результатов косвенных измерений при изменяющихся внешних условиях эксперимента расчет погрешности достаточно проводить для одного из опытов.
8. ГРАФИЧЕСКИЕ МЕТОДЫ ОБРАБОТКИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ В ФИЗИЧЕСКОМ ОПЫТЕ
1. Графики служат простой иллюстрацией изучаемой зависимости (рис.9). По графику можно качественно (а иногда и количественно) установить характер зависимости: сила тока пропорциональна напряжению на участке цепи. 2. Графики можно использовать для нахождения численного значения исследуемой величины. Например, имея в распоряжении график, изображающий зависимость тока от напряжения на однородном участке (рис.9), можно рассчитать сопротивление проводника, исходя из закона Ома.
Для этого на графике выбирают произвольно две точки 1 и 2 и опускают перпендикуляры из этих точек на координатные оси. Затем в масштабе графика находят ∆I, ∆U и рассчитывают сопротивление R. Например, как видно из рис.9, ∆U = 1,0 В; ∆I ≈ 2 мА = 2∙10-3 А. Тогда сопротивление будет равно
Графики следует строить на миллиметровой бумаге с соблюдением ГОСТа.
При построении графиков не следует его загромождать вспомогательными линиями, лишними цифрами и т.п. На координатные оси следует наносить только те числа, которые позволяют: 1. определить масштаб. Например, на рис.12а легко определяется масштаб (вдоль оси абсцисс он составляет 0,2 м1/2, а по оси ординат 0,2 с), тогда, как на другом графике (рис.12б) это сделать практически нельзя. Во-первых, последний график загроможден выносными линиями, на нем не указан масштаб, а просто нанесены числа из табл.8 экспериментальных данных. 2. При построении графиков в физике используют метод сглаживания зависимости. В силу возникающих погрешностей экспериментальные данные ложатся на чертеж с некоторым разбросом. Поэтому линию на графике проводят плавную, следуя ходу экспериментальных точек (рис.13а). На рис.13б тот же график построен не верно – путем соединения всех точек между собой. 3.
 », то получится кривая (рис.14а). При построении графика в координатах «T2 - », то получится кривая (рис.14а). При построении графика в координатах «T2 -  » получим прямую (рис.14б). Естественно, второй метод предпочтительнее перед первым по двум причинам: во-первых, для построения второго графика (рис.14б) требуется меньшее количество экспериментальных точек (для построения прямой достаточно трех точек); во-вторых, определение каких-либо физических величин (например, ускорения свободного падения) упрощается при использовании линейной зависимости. » получим прямую (рис.14б). Естественно, второй метод предпочтительнее перед первым по двум причинам: во-первых, для построения второго графика (рис.14б) требуется меньшее количество экспериментальных точек (для построения прямой достаточно трех точек); во-вторых, определение каких-либо физических величин (например, ускорения свободного падения) упрощается при использовании линейной зависимости.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что значит измерить физическую величину? В чем отличие метода от принципа измерения? 2. Какие измерения называются прямыми и косвенными? Приведите примеры. Существует ли четкая грань между прямыми и косвенными измерениями? Приведите примеры. 3. Какие погрешности встречаются в физическом эксперименте? Каковы причины их возникновения? Какие погрешности называются «промахами» и как от них избавиться? 4. Каковы причины возникновения приборной погрешности? Что принимают за приборную погрешность? 5. Какие погрешности относятся к классу систематических погрешностей и как их можно устранить? Приведите примеры систематических погрешностей (методических и инструментальных). 6. Какие погрешности относятся к случайным? Как можно их уменьшить? 7. Как производится математическая обработка результатов эксперимента при малом числе опытов (n ≤ 30)? 8. Какой вид имеет формула Стьюдента для нахождения случайной погрешности? При каком условии функция распределения Гаусса переходит в формулу Стьюдента? 9. Что называется доверительным интервалом? Как его определить на практике? Что означает запись вида: 10. Что принимают за ошибку прямых измерений, если разброс в значениях отсутствует или очень мал? 11. Как оценивается абсолютная погрешность физических и табличных постоянных? 12. На что указывает абсолютная погрешность и как следует ее округлять? Почему рекомендуется всегда округлять ∆X с избытком? Что называется относительной погрешностью? 13. Как округляют окончательный результат? В каком виде следует представлять окончательный результат? 14. Как производится обработка косвенных измерений? Приведите примеры косвенных измерений при неизменных внешних условиях и в случае меняющихся внешних условий. 15. Какие цели преследует построение графиков в физическом практикуме? Поясните примерами. 16. Какие основные правила следует соблюдать при построении графиков? Проиллюстрируйте примерами. 17. При проведении эксперимента по определению плотности вещества были получены результаты: масса тела m = (5,43 ± 0,05) г и его объем V = (502 ± 6) мм3. Какая из этих величин измерена с более высокой точностью? Как вы это определили? 18. Запишите правильно результаты эксперимента и найдите относительную погрешность для каждого случая? Укажите, какая из приведенных величин измерена с наибольшей точностью.
а) g = (9,798 ± 0,032) м/с2; г) LZ = (72,6 ± 5,3) дБ;
б) u = (227,6 ± 18,7) м/с; д) uзв = (342,62 ± 1,23) м/с;
в) I = (0,03264 ± 0,00023) кг∙м2; е) R = (811,6 ± 24,5) Ом.
ЛАБОРАТОРНАЯ РАБОТА №1
СТАТИСТИЧЕСКИЕ МЕТОДЫ ОБРАБОТКИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ В ФИЗИЧЕСКОМ ЭКСПЕРИМЕНТЕ
Цель работы: 1) изучение закона распределения случайных величин; 2) математическая обработка результатов измерений в физическом эксперименте.
Оборудование: а) счетчик Гейгера, секундомер (задание 1); б) набор резисторов, омметр (задание 2)
Результат измерения физических величин зависит от многих случайных факторов, влияние которых заранее учесть нельзя. Поэтому значения, полученные в физическом эксперименте, являются случайными. Например, счетчик Гейгера регистрирует космические частицы (естественный фон), случайно пролетевшие через счетчик. Причем из опыта в опыт число частиц за одинаковый промежуток времени будет различным. 12 |
|
 Рис. 4
Рис. 4
 (11)
(11) <
<  , то
, то  <<
<<  и за ошибку измерения принимают
и за ошибку измерения принимают  (где С – цена деления прибора) или
(где С – цена деления прибора) или 
 определяют по классу точности, используя формулу (3).
определяют по классу точности, используя формулу (3). >
>  , то приборной погрешностью можно пренебречь, а за погрешность измерений принять
, то приборной погрешностью можно пренебречь, а за погрешность измерений принять  .
.
 - некоторая случайная величина, принимающая ряд значений: X1, X2,…,Xn. Функция
- некоторая случайная величина, принимающая ряд значений: X1, X2,…,Xn. Функция  , характеризующая вероятность попадания случайной величины Xi в единичный интервал значений, называется плотностью вероятности. Тогда вероятность того, что случайная величина Xi попадает в интервал значений
, характеризующая вероятность попадания случайной величины Xi в единичный интервал значений, называется плотностью вероятности. Тогда вероятность того, что случайная величина Xi попадает в интервал значений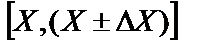
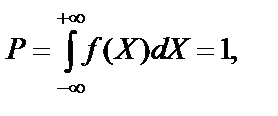
 . Функция f(X) в этом случае называется нормируемой.
. Функция f(X) в этом случае называется нормируемой. Рис. 5
Рис. 5
 (12)
(12) , т.е среднее арифметическое значение является наилучшим приближением к истинному значению (поэтому в качестве оценки результатов измерений в физическом эксперименте принимается среднее арифметическое значение
, т.е среднее арифметическое значение является наилучшим приближением к истинному значению (поэтому в качестве оценки результатов измерений в физическом эксперименте принимается среднее арифметическое значение 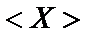 );
);
 ,называется доверительной надежностью (α), где σ – средняя квадратичная погрешность, определяемая по формуле (12). Графически надежность α определяется как площадь под кривой распределения в указанном интервале по отношению ко всей площади (рис.5, заштрихованная площадь). Выражается α в частях (десятичной дробью) или в процентах. (α = 0,85 или α = 85%).
,называется доверительной надежностью (α), где σ – средняя квадратичная погрешность, определяемая по формуле (12). Графически надежность α определяется как площадь под кривой распределения в указанном интервале по отношению ко всей площади (рис.5, заштрихованная площадь). Выражается α в частях (десятичной дробью) или в процентах. (α = 0,85 или α = 85%). , с указанием надежности α.
, с указанием надежности α. поэтому за абсолютную погрешность можно принять
поэтому за абсолютную погрешность можно принять  , при α = 0,67.
, при α = 0,67. = const, растет с увеличением b, т.е. с ростом абсолютной погрешности DХ.
= const, растет с увеличением b, т.е. с ростом абсолютной погрешности DХ.
 . При надежности α = 0,95 коэффициент β = 2 и тогда ∆Χ = 2
. При надежности α = 0,95 коэффициент β = 2 и тогда ∆Χ = 2  .
. . Такие результаты отбрасывают. А значения случайных величин Xi для которых погрешность ∆ Χ< 3σст. оставляют в ряду измеренных. (Например, при ∆Χ = 2
. Такие результаты отбрасывают. А значения случайных величин Xi для которых погрешность ∆ Χ< 3σст. оставляют в ряду измеренных. (Например, при ∆Χ = 2  .)
.) 30) вместо параметра β вводят параметр tα,n, зависящий от числа опытов n и от надежности α. Этот коэффициент tα,n называется коэффициентом Стьюдента и определяется по формуле:
30) вместо параметра β вводят параметр tα,n, зависящий от числа опытов n и от надежности α. Этот коэффициент tα,n называется коэффициентом Стьюдента и определяется по формуле: (14)
(14) ) коэффициент Стьюдента имеет определенное значение, которое находят из справочной табл.50 (прил. IV). Анализ табл.50 показывает, что с ростом числа опытов n при α = const коэффициент tα,n уменьшается, а следовательно, уменьшается и абсолютная погрешность ∆Χсл. Наоборот, при n = const с увеличением α коэффициент tα,n растет.
) коэффициент Стьюдента имеет определенное значение, которое находят из справочной табл.50 (прил. IV). Анализ табл.50 показывает, что с ростом числа опытов n при α = const коэффициент tα,n уменьшается, а следовательно, уменьшается и абсолютная погрешность ∆Χсл. Наоборот, при n = const с увеличением α коэффициент tα,n растет. на величину ∆Χ = 2
на величину ∆Χ = 2  (при α = 0,95), будем считать удовлетворительными.
(при α = 0,95), будем считать удовлетворительными. (15)
(15) (16)
(16) по формуле (16) и сравнив ее с приборной погрешностью ∆Χпр, решаем, можно ли за абсолютную погрешность эксперимента принять случайную погрешность
по формуле (16) и сравнив ее с приборной погрешностью ∆Χпр, решаем, можно ли за абсолютную погрешность эксперимента принять случайную погрешность  (если ∆Χсл > ∆Χпр) или, наоборот, случайной погрешностью можно пренебречь, а за абсолютную погрешность принять ∆Χпр.. Если же
(если ∆Χсл > ∆Χпр) или, наоборот, случайной погрешностью можно пренебречь, а за абсолютную погрешность принять ∆Χпр.. Если же  и ∆Χпр. соизмеримы между собой по величине, то общую (полную) погрешность определяют по формуле (11).
и ∆Χпр. соизмеримы между собой по величине, то общую (полную) погрешность определяют по формуле (11). . Ширину интервала определяют по формуле:
. Ширину интервала определяют по формуле: Рис. 6
Рис. 6
 Рис. 7
Рис. 7
 (18)
(18)
 и ∆
и ∆  = 16,81 м/с. Округляем абсолютную погрешность до первой значащей цифры (разряд десятков): ∆
= 16,81 м/с. Округляем абсолютную погрешность до первой значащей цифры (разряд десятков): ∆  »20 м/с (при этом порядок числа не должен меняться). Среднее значение скорости округляем до разряда десятков:
»20 м/с (при этом порядок числа не должен меняться). Среднее значение скорости округляем до разряда десятков:  ≈ 240 м/с. Результат запишем в виде:
≈ 240 м/с. Результат запишем в виде:  м/с.
м/с. ) до
) до  с доверительной надежностью α. Чтобы истинное значение не «выпало» за пределы этого интервала (ширина интервала равна 2·∆Χ), абсолютную погрешность округляют всегда с избытком, расширяя тем самым границы доверительного интервала.
с доверительной надежностью α. Чтобы истинное значение не «выпало» за пределы этого интервала (ширина интервала равна 2·∆Χ), абсолютную погрешность округляют всегда с избытком, расширяя тем самым границы доверительного интервала. .
.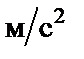 , то
, то 
 ; если g=9,81
; если g=9,81 
 . Другой пример, число π = 3,14. Абсолютная погрешность ∆π = 0,005 и т.д.
. Другой пример, число π = 3,14. Абсолютная погрешность ∆π = 0,005 и т.д. (19)
(19) ), то проведя соответствующие измерения можно установить зависимость исследуемой величины (в нашем примере это период колебаний) от измеряемой величины (длины маятника). Поэтому среднее значение <T> определить не можем и погрешность следует определять для каждого опыта. При этом рассчитывают сначала относительную погрешность
), то проведя соответствующие измерения можно установить зависимость исследуемой величины (в нашем примере это период колебаний) от измеряемой величины (длины маятника). Поэтому среднее значение <T> определить не можем и погрешность следует определять для каждого опыта. При этом рассчитывают сначала относительную погрешность  , где Yi = f(Xi) – функция нескольких переменных; а затем находят абсолютную погрешность
, где Yi = f(Xi) – функция нескольких переменных; а затем находят абсолютную погрешность  .
. 2. Полученное выражение продифференцировать по всем параметрам Xi, входящим в формулу, заменяя при этом значки дифференциала «d» на значок конечного приращения «∆» и все знаки «-» на «+» (погрешности вычитаться не могут):
2. Полученное выражение продифференцировать по всем параметрам Xi, входящим в формулу, заменяя при этом значки дифференциала «d» на значок конечного приращения «∆» и все знаки «-» на «+» (погрешности вычитаться не могут):
 3. Каждое слагаемое возвести в квадрат и из обеих частей извлечь квадратный корень. Формула максимальной относительной погрешности примет вид:
3. Каждое слагаемое возвести в квадрат и из обеих частей извлечь квадратный корень. Формула максимальной относительной погрешности примет вид:
 Значения ∆Χi (где i = 1,2,…,n) прямых измерений определяют по правилам, изложенным в табл.4.
3. Найти абсолютную погрешность ∆yi = εi∙yi и записать результат в виде: y = yi ± ∆yi
Значения ∆Χi (где i = 1,2,…,n) прямых измерений определяют по правилам, изложенным в табл.4.
3. Найти абсолютную погрешность ∆yi = εi∙yi и записать результат в виде: y = yi ± ∆yi


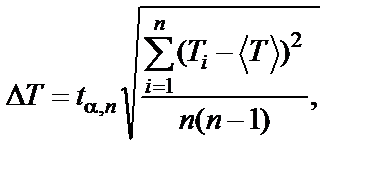
 c.
c.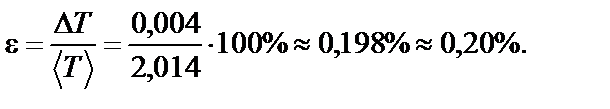

 Рис. 8
Рис. 8
 » (рис.8), который показывает, что зависимость
» (рис.8), который показывает, что зависимость  линейная, т.е. период колебаний пропорционален
линейная, т.е. период колебаний пропорционален  , что соответствует теоретической формуле:
, что соответствует теоретической формуле: . (20)
. (20)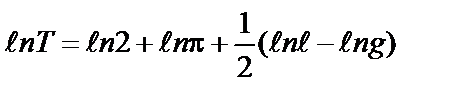

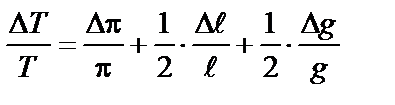
 ,
, , то ∆
, то ∆ 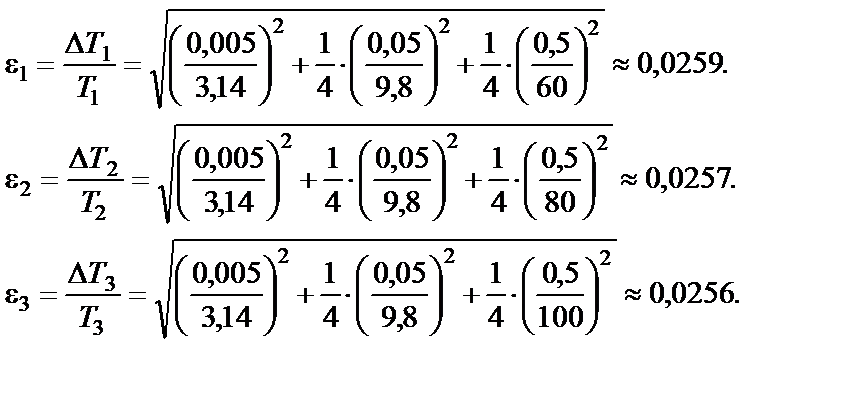
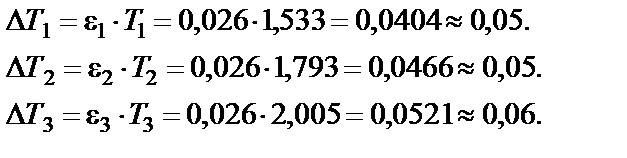
 Рис. 9
Рис. 9
 (21)
(21) .
. Рис. 10
Рис. 10
 Рис. 11
Рис. 11
 Рис. 12
Рис. 12
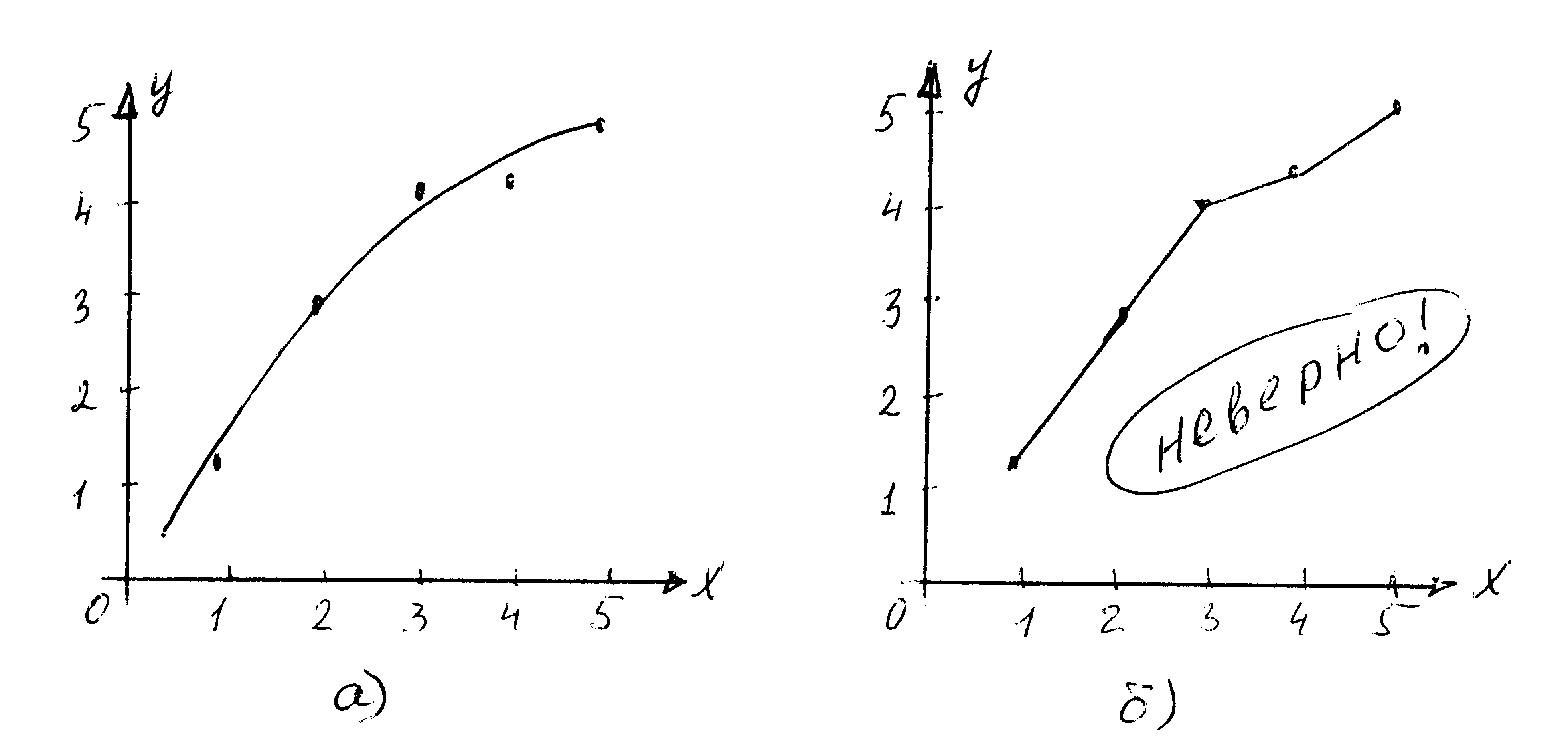 Рис. 13
Рис. 13
 Рис. 14
Рис. 14
 ?
?