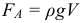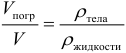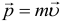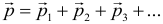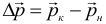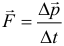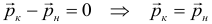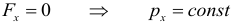|
|
Закон Архимеда. Вес тела в жидкостиК оглавлению... Из–за разности давлений в жидкости на разных уровнях возникает выталкивающая или Архимедова сила, которая вычисляется по формуле:
где: V – объем вытесненной телом жидкости, или же объем погружённой в жидкость части тела, ρ – плотность жидкости в которую погружено тело, и следовательно, ρV – масса вытесненной жидкости. Архимедова сила, действующая на погруженное в жидкость (или газ) тело, равна весу жидкости (или газа), вытесненной телом. Это утверждение, называемоезаконом Архимеда, справедливо для тел любой формы. При этом вес тела (т.е. сила с которой тело действует на опору или подвес) погруженного в жидкость уменьшается. Если принять, что вес покоящегося тела в воздухе равен mg, а именно так мы и будем поступать в большинстве задач (хотя вообще говоря на тело в воздухе также действует очень маленькая сила Архимеда со стороны атмосферы, ведь тело погружено в газ из атмосферы), то для веса тела в жидкости можно легко вывести следующую важную формулу:
Эта формула может быть использована при решении большого количества задач. Ее можно запомнить. При помощи закона Архимеда осуществляется не только мореплавание, но и воздухоплавание. Из закона Архимеда вытекает, что если средняя плотность тела ρт больше плотности жидкости (или газа) ρ (или по–другому mg > FA), тело будет опускаться на дно. Если же ρт < ρ (или по–другому mg < FA), тело будет плавать на поверхности жидкости. Объем погруженной части тела будет таков, что вес вытесненной жидкости равен весу тела. Для подъема воздушного шара в воздухе его вес должен быть меньше веса вытесненного воздуха. Поэтому воздушные шары заполняют легкими газами (водородом, гелием) или нагретым воздухом.
Плавание тел К оглавлению... Если тело находится на поверхности жидкости (плавает), то на него действует всего две силы (Архимеда вверх и тяжести вниз), которые уравновешивают друг друга. Если тело погружено только в одну жидкость, то записав второй закон Ньютона для такого случая и выполнив простые математические операции можем получить следующее выражение связывающее объемы и плотности:
где: Vпогр – объем погруженной части тела, V – полный объем тела. При помощи этого соотношения легко решается большинство задач на плавание тел. Основные теоретические сведения Импульс тела К оглавлению... Импульсом (количеством движения) тела называют физическую векторную величину, являющуюся количественной характеристикой поступательного движения тел. Импульс обозначается р. Импульс тела равен произведению массы тела на его скорость, т.е. он рассчитывается по формуле:
Направление вектора импульса совпадает с направлением вектора скорости тела (направлен по касательной к траектории). Единица измерения импульса – кг∙м/с. Общий импульс системы тел равен векторной сумме импульсов всех тел системы:
Изменение импульса одного тела находится по формуле (обратите внимание, что разность конечного и начального импульсов векторная):
где: pн – импульс тела в начальный момент времени, pк – в конечный. Главное не путать два последних понятия. Абсолютно упругий удар – абстрактная модель соударения, при которой не учитываются потери энергии на трение, деформацию, и т.п. Никакие другие взаимодействия, кроме непосредственного контакта, не учитываются. При абсолютно упругом ударе о закрепленную поверхность скорость объекта после удара по модулю равна скорости объекта до удара, то есть величина импульса не меняется. Может поменяться только его направление. При этом угол падения равен углу отражения. Абсолютно неупругий удар – удар, в результате которого тела соединяются и продолжают дальнейшее своё движение как единое тело. Например, пластилиновый шарик при падении на любую поверхность полностью прекращает свое движение, при столкновении двух вагонов срабатывает автосцепка и они так же продолжают двигаться дальше вместе.
Закон сохранения импульса К оглавлению... При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой. В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой. Этот фундаментальный закон природы называетсязаконом сохранения импульса (ЗСИ). Следствием его являются законы Ньютона. Второй закон Ньютона в импульсной форме может быть записан следующим образом:
Как следует из данной формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Аналогично можно рассуждать для равенства нулю проекции силы на выбранную ось. Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:
Аналогичные записи можно составить и для остальных координатных осей. Так или иначе, нужно понимать, что при этом сами импульсы могут меняться, но именно их сумма остается постоянной. Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны.
|
|