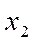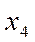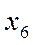|
|
Графический метод решения ЗЛП. Понятие о симплекс-методе
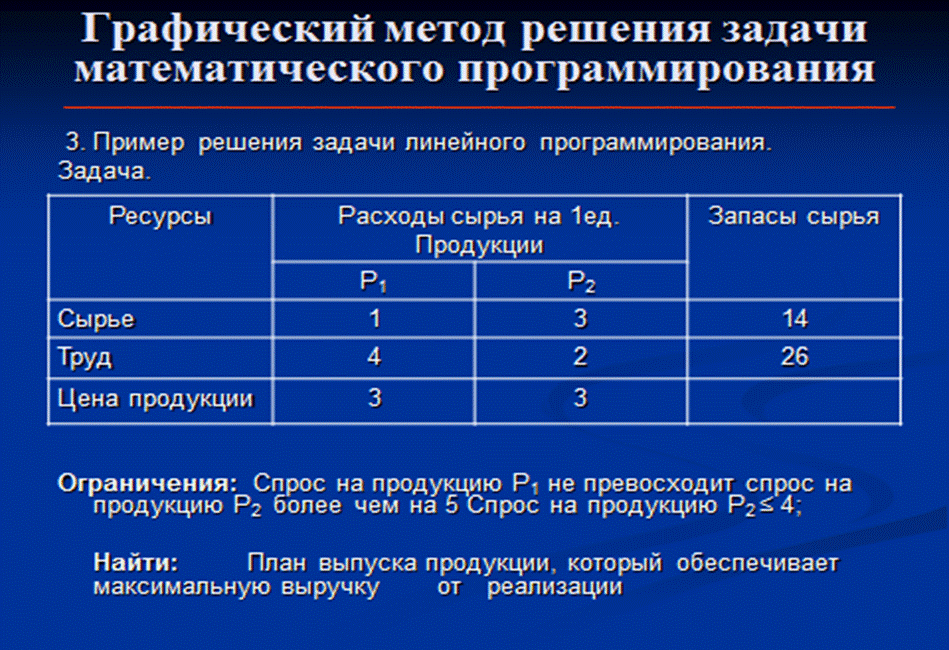
Если число переменных в задаче линейного программирования (ЗЛП) равно двум, а ограничениями является система неравенств, то задачу можно решать графическим методом. Пример 1 При продаже двух видов товара используется 4 типа ресурсов. Норма затрат ресурсов на реализацию единицы товара, общий объем каждого ресурса заданы в табл. 1.
Таблица 1
Прибыль от реализации одной единицы товара первого вида составляет 2 усл. ед., второго вида — 3 усл. ед. Требуется найти оптимальный план реализации товаров, обеспечивающий торговому предприятию максимальную прибыль. Решение. Это задача составления плана при n =2, m=4. Поэтому воспользуемся алгоритмом решения ЗЛП графическим методом. 1) Записывают уравнения прямых, соответствующих ограничениям, и строят их на плоскости. 2) Определяют области, в которых выполняются ограничения задачи. Для этого выбирают произвольную точку на плоскости ХОУ и подставляют ее координаты в левую часть одного из неравенств. Если неравенство верно, то искомая полуплоскость находится с той же стороны от прямой, что и точка; в противном случае искомая полуплоскость лежит с противоположной стороны от прямой. Эти действия последовательно выполняются для всех неравенств, отражающих ограничения задачи. Определяют область допустимых решений задачи, как область пересечения т полуплоскостей, соответствующих т ограничениям. 3) Определяют направление возрастания (убывания) целевой функции. Это можно сделать двумя способами. Можно построить вектор-нормаль к прямой с уравнением целевой функции. Его направление показывает направление возрастания функции, в противоположном направлении функция убывает. Можно просто построить две линии уровня функции 4) Определяют граничную точку (точки) области допустимых решений, в которых целевая функция принимает максимальное или минимальное значение. 5) Вычисляют значения найденной точки, решая совместно уравнения, задающие прямые, на пересечении которых находится эта точка или выявляя уравнение прямой на границе области допустимых решений, с которой совпадает линия уровня целевой функции. Возвращаемся к нашему примеру:
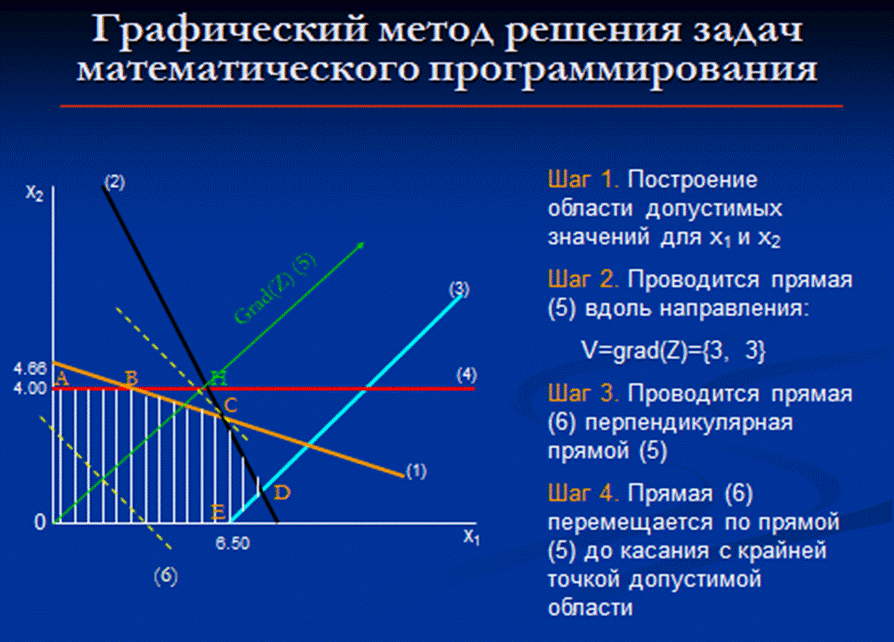
Рис. 1.
Выполнив первые два пункта алгоритма, получим допустимую область ОАВСD ((рис. 1).Целевая функция Р возрастает в направлении вектора n =(2;3) - нормали к прямой 2х1+3х2+с=0, отвечающей целевой функции, следовательно, минимум находится в точке (0;0). Максимум определяем, передвигая нашу линию уровня в направлении вектора n параллельно самой себе до тех пор, пока хотя бы одна ее точка будет принадлежать области допустимых решений. В данном случае это точка х1 = 4, х2 = 2; и при этом Р=2*4+3*2=14. Таким образом, для получения максимальной прибыли в размере 14 усл. ед. надо продать 4 изделия первого вида и 2 изделия второго вида.
Рассмотрим еще один пример.
Изложенный графический метод применим для решения задач линейного программирования следующего вида:
В общем случае линейная математическая модель содержит n переменных и m уравнений. Наиболее распространенный метод ее решения — симплекс-метод. На предыдущем примере мы убедились, что в случае двух переменных область допустимых решений, как правило, представляет собой замкнутый многоугольник. Для n переменных областью допустимых решений является многомерный многогранник, называемый симплексом. Оптимальное решение - это вершина (граничная точка) такого многогранника (в отдельных случаях это целая прямая), поскольку она должна удовлетворять всем ограничениям одновременно. Симплекс-метод и заключается в последовательном целенаправленном обходе вершин симплекса. Благодаря целенаправленности, в каждой следующей граничной точке симплекса значение целевой функции, в общем случае, улучшается.
Для применения симплекс-метода задачу следует записать в канонической форме:
В канонической форме записи все переменные неотрицательны, ограничениями являются уравнения, и требуется найти такие значения хj , при которых целевая функция имеет максимум. Переход к канонической форме записи производится с помощью следующих простых действий. 1) Если требуется найти минимум f, то, заменяя f на (–f), переходят к задаче максимизации, так как min f = max(-f). 2) Если ограничение содержит неравенство со знаком <, то от него переходят к равенству, добавляя в левую часть ограничения дополнительную неотрицательную переменную. 3) Если ограничение содержит неравенство со знаком >, то от него переходят к равенству, вычитая из левой части дополнительную неотрицательную переменную. 4) Если в задаче какая-либо из переменных может принимать и положительные и отрицательные значения, то от нее избавляются, заменяя ее разностью двух других неотрицательных переменных. Например, для произвольной переменной Симплекс-метод является методом направленного перебора решений системы (8) и включает два этапа: · определение начального (базисного) решения, удовлетворяющего ограничениям; · последовательное улучшение начального решения и получение оптимального решения задачи. Любое допустимое решение задачи линейного программирования называется опорным планом задачи. Система (8) содержит т линейно независимых уравнений, их число меньше числа неизвестных, входящих в систему, следовательно, ее можно разрешить относительно т неизвестных, например В итоге систему можно переписать:
(Коэффициенты в полученной системе, естественно, отличны от коэффициентов системы (8), но для простоты обозначены той же буквой). Данный переход осуществляется с помощью элементарных алгебраических преобразований, включающих умножение правой и левой частей уравнений на одно и то же число и их сложение, и не влияющих на значение решений системы (8). После указанных преобразований исходная задача запишется в следующем виде
Форма записи (9) называется стандартной.
Пример.
Запишем задачу в каноническом виде, вводя дополнительные переменные
Для поиска максимума обход «симплекса» будем начинать из начала координат, где все «реальные» переменные, а значит и целевая функция, равны нулю. В итоге на первом шаге базисными (т.е. зафиксированными) будут переменные
Перейдем к составлению симплекс-таблицы (табл. 2). Таблица 2
Для проверки решения на оптимальность просматривается последняя f-строка, которая принимается отвечающей требованию минимизации. Если коэффициенты при свободных переменных в ней неотрицательны, то получено оптимальное решение. Если все эти коэффициенты положительны, то оптимальное решение единственно. Если же среди неотрицательных хотя бы один нулевой, то задача имеет бесконечное множество решений. Если в f-строке есть хотя бы один отрицательный коэффициент, а соответствующем столбце нет ни одного положительного элемента, то целевая функция не ограничена в допустимой области. Если же среди коэффициентов при свободных переменных есть хотя бы один отрицательный и в соответствующем ему столбце есть хотя бы один положительный элемент, то полученное решение может быть улучшено путем ввода соответствующей переменной в базис. Ввод переменной в список базисных переменных означает, что ей приписывается отличное от 0 положительное значение, т.е. ее значение увеличивается. Из формулы для целевой функции f = 5х1 - 2х2 + 3хз видно, что увеличение значения х2 приводит только к уменьшению f т.е. переменную х2 бессмысленно вводить в список базисных переменных. Увеличение переменных х1 и х3 приводит к увеличению значения f при этом на большую величину значение изменяется с увеличением x1 , следовательно, переменная х1 должна стать базисной переменной. Максимальное значение коэффициента при х1 в формуле для f соответствует максимальному по абсолютной величине отрицательному элементу в последней строке симплекс-таблицы, поэтому понятен принцип выбора новой базисной переменной. Для определения переменной, выводимой из списка базисных переменных, надо в соответствии с алгоритмом симплекс-метода найти отношения элементов столбца свободных членов к элементам разрешающего столбца и среди них выбрать минимальное (отрицательный результат деления запрещается назначением ему бесконечной величины). По сути это граница допустимой области в симплексе. В нашем примере
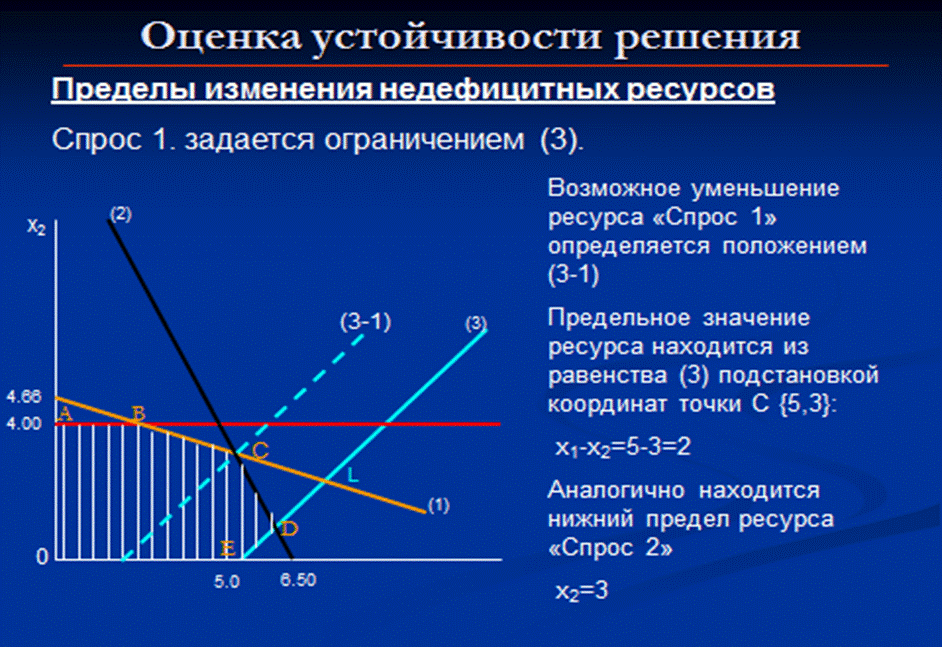
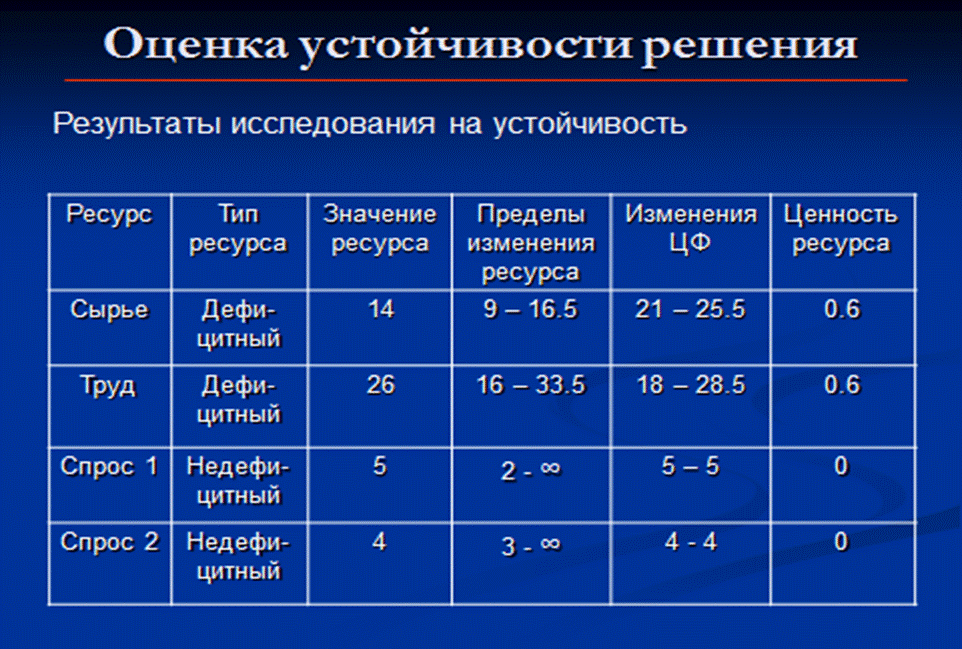
следовательно, из списка базисных переменных надо вывести х4, стоящую в первой строке симплекс-таблицы, и разрешающий элемент a11=3. Решение продолжается аналогичным образом до тех пор, пока в последней строке все элементы не станут неотрицательными. Подробно рассмотрим на практике. Устойчивость решения ЗЛП
12 |
|

 ,
,  где
где  - произвольные константы, и по их расположению определить направление возрастания (убывания) функции Р.
- произвольные константы, и по их расположению определить направление возрастания (убывания) функции Р.



 (8)
(8) , полагают
, полагают 
 где
где 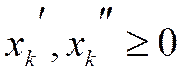 .
. , выразив их через остальные неизвестные (которые и будут базисными).
, выразив их через остальные неизвестные (которые и будут базисными).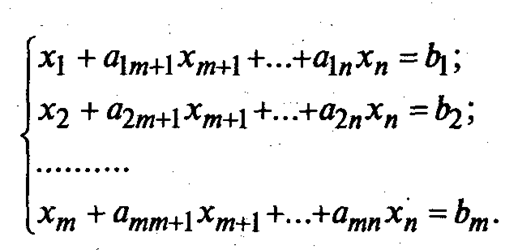

 (9)
(9)
 для перехода к равенствам:
для перехода к равенствам:
 . Свободные же переменные – это
. Свободные же переменные – это  (те, которые изначально определяют целевую функцию и, соответственно, при своем изменении могут изменять ее значение). Раз мы находимся в начале координат, то первый допустимый (опорный) план есть вектор
(те, которые изначально определяют целевую функцию и, соответственно, при своем изменении могут изменять ее значение). Раз мы находимся в начале координат, то первый допустимый (опорный) план есть вектор