|
|
Технический редактор Л.C. БлохинаМАТЕМАТИКА
Часть II
Методические указания по изучению дисциплины и выполнению контрольной работы № 2 для студентов 1-го курса заочной формы обучения МИППС специальностей 130501 Проектирование, сооружение и эксплуатация газонефтепроводов и газонефтехранилищ, 130503 Разработка и эксплуатация нефтяных и газовых месторождений, 130504, Бурение нефтяных и газовых скважин, 130602 Машины и оборудование нефтяных и газовых промыслов, 140101 Тепловые электрические станции, 140104 Промышленная теплоэнергетика, 140211 Электроснабжение, 140607 Электрооборудование автомобилей и тракторов
Краснодар Составители:ассист. В.Н. Лисянская; канд. физ.-мат. наук, доц. И.В. Терещенко
УДК 517
Математика. Часть II: метод. указания [электрон.] по изучению дисциплины и выполнению контрольной работы № 2 для студентов 1-го курса заочной формы обучения МИППС специальностей 130501, 130503, 130504, 130602, 140101, 140104, 140211, 140607 / Сост.: В.Н.Лисянская, И.В.Терещенко; Кубан. гос. технол. ун-т. Каф. общей математики. – Краснодар: Изд. КубГТУ, 2009. – 29 с.
Изложены программа дисциплины, варианты контрольных заданий, темы практических занятий, вопросы к зачету, рекомендуемая литература, приведены примеры выполнения и требования к оформлению контрольной работы.
Ил. 1. Библиогр.: 7 назв.
Печатается по решению методического совета Кубанского государственного технологического университета.
Рецензенты: канд. техн. наук, доц. кафедры ОМ КубГТУ С.М. Силинская; канд. техн. наук, доц. кафедры ПТЭиТЭС КубГТУ С.В. Нестеров
ã КУБГТУ, 2009 Содержание
Инструкция по работе с методическими указаниями В разделе «Программа дисциплины» приведены темы и указывается, что необходимо знать в пределах каждой темы. В конце тем приводятся вопросы для самопроверки и литература из списка рекомендуемой литературы с указанием глав, страниц, где излагается материал темы. Пример Литература: [2, гл.2, c. 3-9], [4, c. 143-162], где 2 и 4 – порядковые номера литературных источников из списка рекомендуемой литературы. Вариант контрольного задания выбирается по последней цифре шифра зачётной книжки. Последняя цифра шифра (0) соответствует 10 варианту в контрольном задании. В разделе «Темы практических занятий» приводятся наименования практических занятий, которые будут проводиться в период экзаменационной сессии, и указывается литература для подготовки. 2 Программа дисциплины Тема 1. Дифференциальное исчисление функции нескольких переменных. Тема 2. Интегральное исчисление функции нескольких переменных. Тема 3. Дифференциальные уравнения. Общие сведения о дифференциальных уравнениях. Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения 1-го порядка: с разделяющимися переменными, однородные, линейные, уравнение Бернулли. Дифференциальные уравнения высших порядков: допускающие понижение порядка. Линейные однородные ДУ второго порядка. Структура общего решения. Линейные однородные ДУ второго порядка с постоянными коэффициентами. Линейные неоднородные ДУ второго порядка с постоянными коэффициентами. Литература: [2, гл. 13, §§2-8,16,20,21], [4, гл. 15, §§1-4]. Вопросы для самоконтроля 1. Определение дифференциального уравнения. 2. Порядок дифференциального уравнения. 3. Решение (общее и частное) дифференциального уравнения. 4. Теорема Коши (о единственности решения задачи Коши). 5. Дифференциальное уравнение с разделяющимися переменными. 6. Линейные дифференциальные уравнения 1-го порядка. Метод Бернулли. 7. Дифференциальные уравнения высших порядков: допускающие понижение порядка. 8. Решение линейного дифференциального уравнения 2-го порядка с постоянными коэффициентами.
Тема 4. Числовые и функциональные ряды. Числовые ряды, их сходимость. Основные понятия и свойства. Необходимые условия сходимости. Остаток ряда. Свойства сходящихся рядов. Знакоположительные ряды. Признаки сравнения. Достаточные признаки Даламбера, Коши, интегральный признак Коши. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимости рядов. Функциональные ряды. Сходимость в точке, радиус сходимости и область сходимости. Степенные ряды. Теорема Абеля. Радиус сходимости и его вычисление. Интервал и область сходимости степенного ряда. Литература: [4, гл. 14, §§1-5], [6, ч.2, гл. III, §§1-4]. Вопросы для самоконтроля 1. Определение числового ряда, общий член ряда, n-я частичная сумма. 2. Сходящиеся и расходящиеся числовые ряды. 3. Гармонический и обобщенный гармонический ряд. 4. Свойства сходящихся рядов. 5. Необходимый признак сходимости. 6. Признаки сравнения (I и II). 7. Признаки Даламбера и Коши (радикальный, интегральный). 8. Знакочередующийся ряд. Признак Лейбница. 9. Абсолютная и условная сходимость. 10. Понятие функционального ряда. Область сходимости. 11. Степенной ряд. Интервал сходимости. Область сходимости. 12. Радиус сходимости и его вычисление (определение, случай Тема 5. Теория вероятностей и математическая статистика. Основные понятия теории вероятностей. Случайные события и операции над ними. Полная группа случайных событий. Классификация определения вероятности. Комбинаторика. Свойства вероятностей. Теорема сложения. Статистическое определение вероятности. Условная вероятность. Теорема умножения. Формула полной вероятности. Формула Байеса. Схема Бернулли повторных испытаний, наивероятнейшее число появлений событий. Локальная и интегральная предельные теоремы и их применение. Случайные величины. Законы распределения дискретных случайных величин. Функция распределения непрерывной случайной величины, ее свойства, плотность вероятности и ее свойства. Нормальный закон распределения и его применение. Математическое ожидание и его свойства. Дисперсия, ее свойства. Выборка и ее графическое представление. Выборочное среднее и дисперсия. Оценка параметров распределения по выборке. Литература: [7, гл.1: §§1-5, гл.2 : §§1-3, гл.3: §§1-5, гл.4: §§1-3, гл.5 §1, гл.6: §§1,2, гл.7: §§1,2]; [8, гл.1 §1, гл.2 §§1-4, гл.3 §1, гл.4 §§1,3]. Вопросы для самоконтроля 1. Определение события (достоверное, невозможное, случайное). 2. Определение события (несовместные, полная группа, противоположные). 3. Классическое определение вероятности. 4. Теорема сложения. 5. Условная вероятность. Теорема умножения. 6. Вероятность хотя бы одного события. 7. Формула полной вероятности. 8. Формула Байеса. 9. Формула Бернулли. Наивероятнейшее число появлений. 10. Дискретная случайная величина. 11. Закон распределения дискретной случайной величины. 12. Математическое ожидание. Его свойства. 13. Дисперсия. Ее свойства. 14. Выборка. Графическое представление выборки. Выборочное среднее и дисперсия. Контрольная работа № 2 Программой дисциплины «Математика» для студентов 1 курса во втором семестре предусмотрено выполнение контрольной работы № 2. При выполнении контрольной работы № 2 необходимо изучить основные понятия и определения функции нескольких переменных. Научится вычислять частные производные. Научиться вычислять двойные интегралы через повторные. Изучить теорию числовых рядов. Необходимо знать основные признаки сходимости числовых рядов. Уметь вычислять радиус сходимости и, пользуясь им, интервал сходимости степенного ряда. Изучить теорию дифференциальных уравнений и научиться находить решения дифференциальных уравнений в простейших случаях. Изучить основные понятия теории вероятности: алгебру случайных событий, вероятность случайного события, условную вероятность случайного события, независимость двух случайных событий. Изучить основные понятия, связанные со случайными величинами. Уметь вычислять по известному закону распределения математическое ожидание и дисперсию. Задание № 1. Найти частные производные первого порядка. Пример. Вычислим частные производные первого порядка
При вычислении частной производной по переменной
Задание № 2. Вычислить двойной интеграл. Пример. Вычисляем двойной интеграл по прямоугольнику через один из повторных интегралов:
При интегрировании по
Вновь применяя формулу Ньютона –Лейбница уже к внешнему интегралу, получим
Задание № 3. Найти общее решение дифференциального уравнения 1-го порядка. Пример 1. Преобразуем уравнение к виду
Сделав подстановку
Разделяя переменные, получим
Интегрируя, имеем:
Отсюда
Учитывая, что Пример 2. Это уравнение является уравнением Бернулли
Выберем функцию
Выбирая простейшие решение
откуда
Таким образом, получаем общее решение дифференциального уравнения
Задание № 4. Найти общее решение дифференциального уравнения 2-го порядка. Пример. Положим
Исходное уравнение примет вид
Разделяя переменные, найдем
Заменив
откуда
Разделив переменные, получим общее решение исходного уравнения в неявном виде:
Задание № 5.Найти частное решение линейного дифференциального уравнения Пример. Найти общее решение дифференциального уравнения Найдем решение
где По корням характеристического уравнения составим общее решение однородного уравнения
Найдем
Поэтому положим
Так как
подставим их в уравнение
После группировки по степеням
Два многочлена одинаковой степени равны, когда равны их коэффициенты при одинаковых степенях неизвестных. Приравняем коэффициенты при степенях
Отсюда
Для нахождения решения, удовлетворяющего начальным условиям, найдем первую производную:
Подставляя в начальные условия
Отсюда окончательно находим
Задание № 6. Исследовать сходимость числового ряда Пример 1. Исследовать сходимость числового ряда Применим признак Даламбера: имеем
Поэтому по признаку Даламбера ряд Пример 2. Исследования сходимость числового ряда Применим интегральный признак Маклорена - Коши, составив функцию
Так как на интервале
Данный интеграл сходится, так как
поэтому сходится и данный ряд. Задание № 7. Найти интервал сходимости степенного ряда Пример. Найти интервал сходимости степенного ряда Выпишем коэффициенты ряда:
Подставим их в формулу для радиуса сходимости степенного ряда:
Следовательно, ряд сходится для значений Если Задание № 8. Решить задачу по теории вероятности. Пример 1. Для приема зачета преподаватель заготовил 50 задач: 10 задач по пределам функций, 20 задач по дифференциальному исчислению и 20 задач по интегральному исчислению. Для сдачи зачета студент должен решить первый же доставшийся наугад билет из трех задач по одной задаче на каждую тему. Какова вероятность для студента сдать зачет, если он может решить пять задач по пределам, 18 задач по дифференциальному исчислению и 15 задач по интегральному исчислению? Решение. Число билетов, которое может составить преподаватель, равно
Число билетов, которое знает студент равно
Считая, что студенту билет достается случайным образом и что это равновероятные события, получаем вероятность сдачи зачета:
Пример 2. Для приема зачета преподаватель заготовил 50 задач: 10 задач по пределам функций, 20 задач по дифференциальному исчислению, 20 по интегральному исчислению. Для сдачи зачета студент должен решить первую же доставшуюся наугад задачу. Какова вероятность для студента сдать зачет, если он может решить пять задач по пределам, 18 задач по дифференциальному исчислению и 15 задач по интегральному исчислению? Решение № 1. Студент знает 38 задач из пятидесяти, поэтому вероятность сдать зачет равна Решение № 2. Вероятность получить задачу по пределам (событие
События
находим вероятность сдачи зачета
Пример № 3. В студенческой группе 25 человек, из них 15 студентов и 10 студенток. Наугад выбирается делегация на студенческую конференцию в составе четырёх человек. Какова вероятность, что изберут двух студентов и двух студенток? Решение. Число способов выбрать четырёх человек в делегацию из 25 человек в группе равно числу сочетаний четырёх предметов из 25:
Аналогично находим число способов выбрать в делегацию двух студентов из 15:
и двух студенток из 10:
Следовательно, число способов выбрать делегацию из четырёх человек, в составе которой две студентки и два студента равно
Считая, что исходы выборов равновероятны, получаем вероятность такого выбора:
Пример № 4. В автоколонне 10 автобусов. Вероятность того, что у автобуса на линии не будет поломок в течение одной смены, равна Решение. Вероятность того, что у
Тогда искомая вероятность равна
Пример № 5. Вероятность изготовления на станке нестандартного изделия равна Решение. Пусть случайная величина
где
Подставляя значения, находим
Значение функции Лапласа Задание № 9. Задана непрерывная случайная величина 1) найти плотность распределения вероятностей 2) схематично построить графики функций 3) найти математическое ожидание, дисперсию и среднее квадратичное отклонение случайной величины Пример. Решить задание № 9, если задана непрерывная случайная величина
1) Плотность распределения случайной величины равна первой производной от функции распределения.
Проверим условие нормировки
Подставив сюда найденную плотность распределения, получим
2) Строим схематично графики функций
Рисунок 1 - Графики функций распределения 3) Для нахождения математического ожидания используем формулу
Замечание. Для вычисления интегралов использовались формулы:
Задание № 10. Заданы математическое ожидание Пример. Заданы математическое ожидание 1. Написать плотность распределения вероятностей и схематично построить ее график. 2. Найти вероятность того, что 3. Найти вероятность того, что 4. Найти интервал, симметричный относительно математического ожидания, в котором с вероятностью g=0,95 будут заключены значения величины 1) Составим функцию плотности распределения случайной величины Х с параметрами
Построим схематически график функции
Рисунок 2 - График функции 2) Вероятность попадания нормальной величины
где
Тогда вероятность попадания в интервал
Значения функций найдены по таблице приложения 2 [7, стр. 462]. 3) Аналогично находим вероятность попадания в интервал
В нашем случае
По таблице [7, стр. 462] найдем аргумент t, при котором
Задание № 11.Заданы среднее квадратичное отклонение Пример. Найти доверительный интервал для оценки с надежностью Требуется найти доверительный интервал
По таблице значений функции Лапласа находим Темы практических занятий
1. Функции нескольких переменных. Область определения, пределы, непрерывность. Частные производные первого и второго порядков. Экстремумы функции двух переменных. 2. Дифференциальные уравнения с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка. Линейные дифференциальные уравнения первого порядка. Уравнение Бернулли. Уравнения старших порядков, допускающие понижение порядка. Линейные дифференциальные уравнения с постоянными коэффициентами и специальной правой частью. 3. Признаки сходимости знакопостоянных рядов. Абсолютно и неабсолютно сходящиеся ряды. Признак сходимости Лейбница. Степенные ряды. Радиус и интервал сходимости. Ряды Тейлора. Вычисление значений функций и интегралов с помощью степенных рядов. Нахождение решений дифференциальных уравнений с помощью степенных рядов. 4. Классическая вероятностная схема. Условные вероятности. Независимость случайных событий. Формула полной вероятности и формула Байеса. Повторные испытания. Формула Бернулли и формула Пуассона. Локальная и интегральная теоремы Лапласа-Муавра. Дискретные и непрерывные случайные величины. Среднее значение и дисперсия. Элементы математической статистики. Выборка и ее представление. Выборочное среднее и выборочная дисперсия. Оценка параметров распределения по выборке. Содержание и оформление контрольных работ 1. Требования к оформлению контрольных работ: контрольные работы могут выполняться на электронных носителях или в тетради (12 л.), на обложке необходимо указать номер контрольной работы, свой факультет, специальность, шифр зачетной книжки, номер варианта, свою фамилию, имя, отчество. 2. Требования к выполнению контрольной работы: - при выполнении работы необходимо приводить основные теоретические моменты, промежуточные математические доказательства, методики, формулы, расчеты. - в конце работы указывается список использованных источников, ставится число и личная подпись.
Вопросы для подготовки к экзамену 1. Функции нескольких переменных, основные понятия и определения. 2. Частные производные первого и второго порядков функции нескольких переменных. 3. Дифференциалы первого и второго порядков функции нескольких переменных. 4. Экстремумы функции двух переменных. 5. Двойные интегралы и их свойства. Вычисление двойного интеграла через повторные. 6. Замена переменных в двойном интеграле. Приложения двойных интегралов. 7. Тройные интегралы и их свойства. Вычисление тройного интеграла через повторные. 8. Замена переменных в тройном интеграле. Приложения тройных интегралов. 9. Задачи, приводящие к дифференциальным уравнениям. Основные определения и понятия теории дифференциальных уравнений. 10. Дифференциальные уравнения с разделяющимися переменными. Дифференциальные уравнения вида 11. Однородные дифференциальные уравнения первого порядка. 12. Линейные дифференциальные уравнения первого порядка. Уравнение Бернулли. 13. Уравнения старших порядков, допускающие понижение порядка. |
|
 ,
,  ).
). .
. и
и  . При вычислении частной производной по переменной
. При вычислении частной производной по переменной 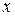 вторая переменная
вторая переменная  считается постоянной величиной. Тогда по правилам дифференцирования получим:
считается постоянной величиной. Тогда по правилам дифференцирования получим: .
. .
. .
. .
. .
. .
. .
. :
: .
.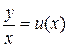 или
или  , получим, подставив в уравнение,
, получим, подставив в уравнение, .
.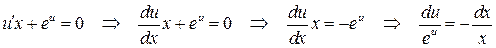 .
. .
. .
.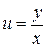 , получаем общее решение заданного уравнения
, получаем общее решение заданного уравнения  .
. .
. , где
, где  ,
, 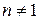 ,
,  и
и  - непрерывные функции. Положим
- непрерывные функции. Положим  . Тогда получим
. Тогда получим или
или  .
.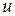 как частное решение уравнения
как частное решение уравнения  . Разделяя переменные, получим
. Разделяя переменные, получим
 .
. , находим
, находим  . Для оставшейся части уравнения получим
. Для оставшейся части уравнения получим  , где
, где  . Разделяя переменные, получим
. Разделяя переменные, получим ,
, .
. , где
, где 
 .
. .
. . Тогда
. Тогда .
.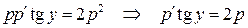 .
. .
. на
на  , получим
, получим ,
, . Здесь уже допускается
. Здесь уже допускается  , так как уравнение
, так как уравнение 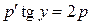 , очевидно, имеет решение
, очевидно, имеет решение  . Заменим обратно
. Заменим обратно 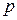 на
на 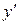 , тогда получим уравнение первого порядка:
, тогда получим уравнение первого порядка: .
. .
. , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям  ,
,  .
. с начальными условиями
с начальными условиями  и
и 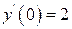 .
. однородного уравнения, для чего составим и решим характеристическое уравнение:
однородного уравнения, для чего составим и решим характеристическое уравнение: ,
,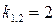 корень кратности 2.
корень кратности 2. :
: .
.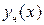 - частное решение неоднородного уравнения. Так как среди корней характеристического уравнения нет
- частное решение неоднородного уравнения. Так как среди корней характеристического уравнения нет  , то частное решение будем искать в виде, похожем на правую часть неоднородного уравнения. Там находится выражение
, то частное решение будем искать в виде, похожем на правую часть неоднородного уравнения. Там находится выражение 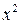 - многочлен второй степени, общий вид которого
- многочлен второй степени, общий вид которого .
. .
. есть решение неоднородного дифференциального уравнения
есть решение неоднородного дифференциального уравнения  ,
,  :
: ;
; .
. .
. в обеих частях:
в обеих частях: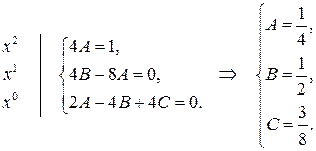
 . Общее решение
. Общее решение .
. .
. или
или 
 .
. .
.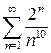 .
.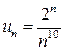 ,
, 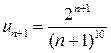 ,
,  . Тогда
. Тогда .
.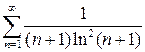 .
. .
. эта функция
эта функция  и с ростом
и с ростом  .
. ,
, .
. .
. ,
,  .
. .
. . Исследуем сходимость ряда на концах промежутка. Если
. Исследуем сходимость ряда на концах промежутка. Если  , то получим обобщенный гармонический ряд
, то получим обобщенный гармонический ряд  , который сходится, так как
, который сходится, так как  .
.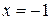 , то получим знакопеременный ряд
, то получим знакопеременный ряд  , который сходится, так как удовлетворяет условиям признака Лейбница.
, который сходится, так как удовлетворяет условиям признака Лейбница. .
. .
. .
. .
. ) равна
) равна  , вероятность получить задачу по дифференциальному исчислению (событие
, вероятность получить задачу по дифференциальному исчислению (событие  )равна
)равна 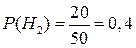 =0,4, вероятность получить задачу по интегральному исчислению (событие
=0,4, вероятность получить задачу по интегральному исчислению (событие  ) равна
) равна  . Если событие
. Если событие  означает, что задача решена, то условные вероятности решить задачу при условии, что это задача по пределам, дифференциальному или интегральному исчислению, соответственно равны:
означает, что задача решена, то условные вероятности решить задачу при условии, что это задача по пределам, дифференциальному или интегральному исчислению, соответственно равны: ;
; 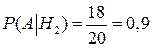 ;
;  .
.
 .
. .
.
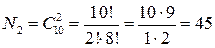 .
. .
.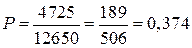 .
. . Какова вероятность того, что в течение смены поломок не будет не менее чем у девяти автобусов?
. Какова вероятность того, что в течение смены поломок не будет не менее чем у девяти автобусов? автобусов не будет поломок в течение смены, определяется формулой Бернулли:
автобусов не будет поломок в течение смены, определяется формулой Бернулли: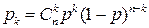 .
. или
или .
. . Какова вероятность обнаружить в партии из 1000 изделий, изготовленных на таком станке, от 940 до 960 стандартных изделий?
. Какова вероятность обнаружить в партии из 1000 изделий, изготовленных на таком станке, от 940 до 960 стандартных изделий? есть число стандартных деталей, обнаруженных в партии. При большом числе изделий в партии
есть число стандартных деталей, обнаруженных в партии. При большом числе изделий в партии  и вероятности изготовления стандартной детали
и вероятности изготовления стандартной детали  близкой к единице, можно использовать интегральную формулу Муавра – Лапласа для определения вероятности того, что число стандартных изделий окажется между
близкой к единице, можно использовать интегральную формулу Муавра – Лапласа для определения вероятности того, что число стандартных изделий окажется между  и
и  :
: ,
, - функция Лапласа:
- функция Лапласа: .
.
 .
.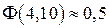 находим из таблицы приложения 2 [7, стр. 462].
находим из таблицы приложения 2 [7, стр. 462]. . Требуется:
. Требуется: ;
;

 .
. .
.
 .
. , где a, b - начало и конец интервала, на котором определена плотность распределения
, где a, b - начало и конец интервала, на котором определена плотность распределения  ;
;
 ,
, .
. ,
, ,
, ,
, .
. и среднее квадратичное отклонение
и среднее квадратичное отклонение  нормально распределенной случайной величины
нормально распределенной случайной величины  .
. и среднее квадратичное отклонение
и среднее квадратичное отклонение  нормально распределенной случайной величины Х.
нормально распределенной случайной величины Х. :
: .
. . Обратим внимание на то, что нормальная кривая симметрична относительно прямой
. Обратим внимание на то, что нормальная кривая симметрична относительно прямой  и достигает максимального значения в этой точке, равного
и достигает максимального значения в этой точке, равного  , т.е.
, т.е. 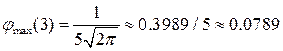 . На кривой находятся две точки перегиба
. На кривой находятся две точки перегиба  с ординатой
с ординатой  . Построим график
. Построим график 
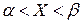 равна
равна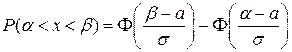 ,
, равна
равна
 .
. :
: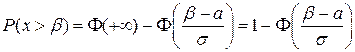 .
. ,
,  .
. 4) Воспользуемся формулой
4) Воспользуемся формулой  . Из нее следует, что вероятность попадания в интервал, симметричный относительно математического ожидания, равна
. Из нее следует, что вероятность попадания в интервал, симметричный относительно математического ожидания, равна .
.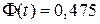 . Получим
. Получим 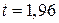 . Тогда
. Тогда  . Таким образом, получаем, что интервал
. Таким образом, получаем, что интервал  совпадает с интервалом
совпадает с интервалом  . Отсюда
. Отсюда .
. и объем выборки
и объем выборки 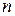 . Найти доверительный интервал для оценки неизвестного математического ожидания
. Найти доверительный интервал для оценки неизвестного математического ожидания  .
.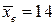 и объем выборки
и объем выборки 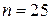 .
.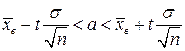 . Все величины, кроме коэффициента
. Все величины, кроме коэффициента  , известны. Найдем
, известны. Найдем 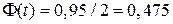 , где
, где  .
. .
.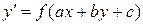 .
.