|
|
VIII. Обыкновенные дифференциальные уравнения39. Физические задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения первого порядка. Задача Коши. Теорема существования и единственности решения задачи Коши. Понятие об основных решениях дифференциальных уравнений. Основные классы уравнений, интегрируемых в квадратурах. 40. Дифференциальные уравнения высших порядков. Задача Коши. Уравнения, допускающие понижение порядка. 41. Линейные дифференциальные уравнения, однородные и неоднородные. Понятие общего решения. Метод Лагранжа вариации произвольных постоянных. 42. Линейные дифференциальные уравнения с постоянными коэффициентами. Уравнения с правой частью специального вида.
IX. Системы обыкновенных дифференциальных уравнений 43. Задача Коши для нормальной системы дифференциальных уравнений. Теорема существования и единственности решения задачи Коши. Метод исключения. Векторно-матричная запись нормальной системы. Структура общего решения. 44. Нормальные системы линейных дифференциальных уравнений с постоянными коэффициентами. Решение в случае простых корней характеристического уравнения. X. Числовые ряды. Степенные ряды 45. Числовые ряды. Сходимость и сумма ряда. Необходимое условие сходимости. Действия с рядами. 46. Ряды с положительными членами. Признаки сходимости. 47. Знакопеременные ряды. Абсолютная и условная сходимости. Знакочередующиеся ряды. Признак Лейбница. 48. Степенные ряды. Теорема Абеля. Радиус сходимости. Свойства степенных рядов. 49. Разложение функции в степенные ряды. Ряд Тейлора. Применение степенных рядов к приближенным вычислениям.
XI. Ряды Фурье 50. Тригонометрическая система функций. Ряд Фурье. Разложение функции в ряд Фурье. Формулировка условий разложимости в ряд Фурье.
XII. Кратные интегралы 51. Задачи, приводящие к понятию кратного интеграла. Двойные и тройные интегралы, их основные свойства. 52. Вычисление двойных и тройных интегралов в декартовых координатах. 53. Применение кратных интегралов для вычисления объемов и площадей, для решения задач механики и физики.
XIII. Криволинейные и поверхностные интегралы 54. Задачи, приводящие к криволинейным интегралам. Определение криволинейных интегралов первого и второго рода, их основные свойства и вычисление. Геометрические и механические приложения. Формула Грина. 55. Поверхностные интегралы, их свойства и вычисление.
XIV. Векторный анализ 56. Скалярное поле. Поверхности и линии уровня скалярного поля. Производная по направлению. Градиент скалярного поля. 57. Векторное поле. Векторные линии и их дифференциальные уравнения. 58. Односторонние и двусторонние поверхности. Поток векторного поля Теорема Остроградского. 59. Дивергенция векторного поля, ее инвариантное определение и физический смысл. Вычисление дивергенции. Соленоидальные (трубчатые) поля. 60. Линейный интеграл в векторном поле. Работа силового поля. Циркуляция векторного поля. Ротор векторного поля. Теорема Стокса. 61. Потенциальное поле. Условие потенциальности поля. Вычисление линейного интеграла в потенциальном поле.
Контрольная работа №1 Тема1. Аналитическая геометрия. Элементы векторной и линейной алгебры. Комплексные числа.
Основные теоретические сведения
1. Определителем
и вычисляемое, согласно указанному ниже правилу, по заданным числам Минором Алгебраическое дополнение
Рекуррентная формула для вычисления определителя
(разложение определителя по элементам
2. Скалярным произведением двух векторов
где
3. Векторным произведением векторов 1) 2) 3)
4. Смешанное произведение трех векторов
Модуль смешанного произведения равен объему параллелепипеда, построенного на векторах.
5. Выражение вида
Извлечение корня
где
Пример 1.Дана система линейных алгебраических уравнений:
Проверить, совместна ли эта система, и в случае совместности решить ее: а) по формулам Крамера; б) методом Гаусса; в) с помощью обратной матрицы. Совместность данной системы проверим по теореме Кронекера - Капелли. Решение. С помощью элементарных преобразований найдем ранг матрицы
данной системы и ранг расширенной матрицы
Для этого умножим первую строку матрицы В на –2 и сложим со второй, затем умножим первую строку на –3 и сложим с третьей, получим
Следовательно, rang A = rang B = 3 (числу неизвестных), исходная система имеет единственное решение. а) Находим решение системы по формулам Крамера
где
б) Метод Гаусса. Составим расширенную матрицу и проведем необходимые элементарные преобразования. Элементы первой строки умножим на –2 и прибавим к соответствующим элементам 2-ой строки, затем элементы первой строки умножим на –3 и прибавим к соответствующим элементам третьей строки.
Последней матрицей соответствует система, эквивалентная исходной:
Из этой системы, двигаясь снизу вверх, последовательно находим:
в) Матричный метод. Так как det A = -16 ¹0, то матрица А невырожденная, существует обратная матрица А-1, определяемая по формуле:
где Введем в рассмотрение матрицы столбцы для неизвестных и свободных членов:
Тогда данную систему можно записать в матричной форме:
Решение системы:
таким образом,
Пример 2.Составить канонические уравнения: а) эллипса, большая ось которого равна 5, а фокус находится в точке F(3,0); б) гиперболы с мнимой осью в=3 и а) Каноническое уравнение эллипса имеет вид
б) Каноническое уравнение гиперболы имеет вид
в) Каноническое уравнение параболы в данном случае имеет вид y2=2px, а уравнение ее директрисы
1) Угол между ребрами AB и AD вычисляем по формуле:
где
2) Уравнение плоскости, проходящей через три заданные точки имеет вид:
Подставляя в данное уравнение координаты точек А,В и С, получим:
Разложив определитель по элементам первой строки, получим:
отсюда находим искомое уравнение плоскости АВС:
3) Угол между ребром AD и гранью АВС вычисляем по формуле:
где
4) Площадь грани АВС вычисляется по формуле:
Окончательно имеем
5) Объем пирамиды вычисляем по формуле:
Объем пирамиды равен 24 (куб. ед.). 6) Уравнение высоты DM, опущенной из вершины D на грань АВС составляет по формуле
где (x0, y0, z0) – координаты точки D,
Введение в анализ. Дифференциальное исчисление функции одной переменной.
Основные теоретические сведения
1. Схема полного исследования функции и построение ее графика. Для полного исследования функции и построения ее графика можно рекомендовать следующую примерную схему: 1) указать область определения; 2) найти точки разрыва функции, точки пересечения ее графика с осями координат; 3) установить наличие или отсутствие четности, нечетности, периодичности функции; 4) найти асимптоты графика функции; 5) исследовать функцию на монотонность и экстремум; 6) определить интервалы выпуклости и вогнутости; 7) построить график функции. 2. Правила дифференцирования. Если
3. Таблица производных основных элементарных функций 1. 3. 5. 7. 9. 11. 13.
Пример 1.Найти указанные пределы.
Решение: а) б) г)
Пример 2.Исследовать функцию Решение: для точки x1 = 3 имеем:
точка При
Пример 3.Найти производную функции Решение.Логарифмируя данную функцию, получаем:
Дифференцируем обе части последнего равенства по х:
Отсюда
Далее
Окончательно имеем:
Пример 4.Найти производную функции y, если Дифференцируем обе части данного уравнения по
Отсюда находим
15.
Контрольная работа №1 Задание №1 Данную систему уравнений исследовать и решить тремя способами: а) по формулам Крамера; б) методом Гаусса; в) средствами матричного исчисления.
11. 13. 15. 17. 19. 21. 23. 25. 27. 29.
Задание №2 Даны координаты вершин треугольника ABC. Найти: 1) длину стороны АВ; 2) уравнение стороны АВ; 3) уравнение высоты СН; 4) уравнение медианы АМ; 5) точку N пересечения медианы АМ и высоты СН; 6) уравнение прямой, проходящей через вершину С параллельно стороне АВ.
Задание №3В пространстве заданы точки
1. А(3,3,2); В(5,1,7); С(2,4,1) 2. А(6,5,1); В(8,6,7); С(8,2,4) 3. А(8,8,4); В(6,6,5); С(5,7,1) 4. А(4,1,6); В(4,4,5); С(3,8,2) 5. А(1,4,6); В(1,5,6); С(6,7,2) 6. А(4,3,3); В(5,6,2); С(1,8,2) 7. А(3,4,2); В(4,4,4); С(2,3,4) 8. А(1,1,2); В(2,7,8); С(7,5,5) 9. А(1,4,4); В(5,2,1); С(7,6,8) 10. А(8,5,5); В(6,7,2); С(2,2,3) 11. А(5,1,6); В(2,8,6); С(7,7,5) 12. А(3,3,2); В(6,5,5); С(4,3,3) 13. А(3,3,2); В(5,1,7); С(9,2,4) 14. А(1,6,5); В(1,8,6); С(7,8,9) 15. А(2,4,9); В(8,9,8); С(4,6,6) 16. А(5,5,7); В(1,4,1); С(6,4,4) 17. А(5,3,8); В(2,1,4); С(6,1,5) 18. А(6,6,0); В(7,2,4); С(3,3,5) 19. А(6,2,1); В(8,2,3); С(4,2,4) 20. А(4,9,0); В(4,0,0); С(2,9,3) 21. А(4,1,1); В(2,2,7); С(8,9,7) 22. А(4,5,0); В(1,4,4); С(5,2,1) 23. А(7,6,8); В(8,0,3); С(3,2,5) 24. А(7,1,4); В(1,6,4); С(4,5,3) 25. А(6,0,7); В(2,4,3); С(3,5,6) 26. А(-3,3,-2); В(7,-1,7); С(2,4,10) 27. А(-6,5,1); В(8,6,7); С(8,2,4) 28. А(8,-8,4); В(6,6,5); С(5,7,1) 29. А(3,1,6); В(4,2,5); С(3,11,2) 30. А(10,4,-6); В(1,5,6); С(6,5,-2)
Задание №4 Найти указанные пределы (не пользуясь правилом Лопиталя):
Задание №5 Найти производные |
|
 -го порядка называется число
-го порядка называется число  , записываемое в виде квадратичной таблицы
, записываемое в виде квадратичной таблицы
 , которые называются элементами определителя. Индекс
, которые называются элементами определителя. Индекс  указывает номер строки, а
указывает номер строки, а  – номер столбца квадратной таблицы.
– номер столбца квадратной таблицы. элемента
элемента  порядка, получаемый из определителя
порядка, получаемый из определителя  элемента
элемента  .
.
 и
и 
 называется число, определяемое равенством
называется число, определяемое равенством ,
, – угол между векторами
– угол между векторами  и
и 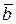 .
. , обозначаемый
, обозначаемый  , который удовлетворяет условиям:
, который удовлетворяет условиям: ,
,  ;
; ;
; – правая тройка векторов;
– правая тройка векторов;
 – формула для вычисления площади треугольника.
– формула для вычисления площади треугольника. есть число, равное
есть число, равное .
. называется комплексным числом (в алгебраической и тригонометрической форме соответственно). Здесь
называется комплексным числом (в алгебраической и тригонометрической форме соответственно). Здесь  ,
,  – действительная часть,
– действительная часть,  – мнимая часть комплексного числа
– мнимая часть комплексного числа 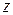 ;
;  и
и  – модуль и аргумент числа
– модуль и аргумент числа  ;
; 
 .
. производится по формуле
производится по формуле ,
,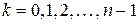 .
.


 ~
~  ~
~ 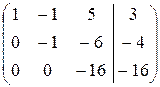 .
.


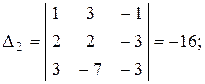


 ~
~  ~
~ 


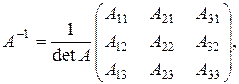

 являются алгебраическими дополнениями соответствующих элементов матрицы А.
являются алгебраическими дополнениями соответствующих элементов матрицы А.
 , отсюда находим
, отсюда находим 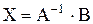 - решение системы в матричной форме.
- решение системы в матричной форме.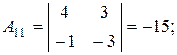







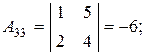



 ; в) параболы, имеющей директрису x=-3.
; в) параболы, имеющей директрису x=-3. . По условию задачи большая полуось а=5, с=3. Для эллипса выполняется равенство
. По условию задачи большая полуось а=5, с=3. Для эллипса выполняется равенство  . Подставив значения а и с, найдем в2=16. Искомое уравнение эллипса:
. Подставив значения а и с, найдем в2=16. Искомое уравнение эллипса: .
. . По условию задачи мнимая полуось в=3, эксцентриситет
. По условию задачи мнимая полуось в=3, эксцентриситет  и учитывая, что
и учитывая, что  , находим а2 = 16. Искомое уравнение гиперболы:
, находим а2 = 16. Искомое уравнение гиперболы: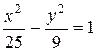 .
. . По условию x=-3, следовательно,
. По условию x=-3, следовательно,  , уравнение параболы имеет вид
, уравнение параболы имеет вид  .
. Пример 3.Даны координаты вершин пирамиды ABCD: A(2,1,0), B(3,-1,2), C(13,3,10), D(0,1,4). Найти: 1) угол между ребрами AB и AD; 2) уравнение плоскости АВС; 3) угол между ребром AD и гранью АВС; 4) площадь грани АВС; 5) объем пирамиды; 6) уравнение высоты, опущенной из вершины AD на грань АВС.
Пример 3.Даны координаты вершин пирамиды ABCD: A(2,1,0), B(3,-1,2), C(13,3,10), D(0,1,4). Найти: 1) угол между ребрами AB и AD; 2) уравнение плоскости АВС; 3) угол между ребром AD и гранью АВС; 4) площадь грани АВС; 5) объем пирамиды; 6) уравнение высоты, опущенной из вершины AD на грань АВС. ,
,
 .
. ;
; .
. .
.
 ,
, .
.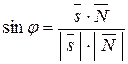 ,
, - направляющий вектор ребра AD,
- направляющий вектор ребра AD,  - нормальный вектор грани АВС.
- нормальный вектор грани АВС. .
. .
. .
.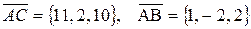 .
. .
.
 .
. .
. ,
, - координаты направляющего вектора прямой DM. Т.к. DM ^ АВС, то в качестве направляющего вектора
- координаты направляющего вектора прямой DM. Т.к. DM ^ АВС, то в качестве направляющего вектора  можно взять нормальный вектор
можно взять нормальный вектор  .
.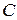 – постоянное число и
– постоянное число и  ,
,  – некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
– некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования: .
.
 .
.
 .
.
 .
.
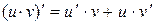 .
.
 .
.
 . 2.
. 2.  .
. . 4.
. 4.  .
. . 6.
. 6.  .
.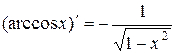 . 8.
. 8.  .
. . 10.
. 10.  .
.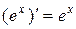 . 12.
. 12. 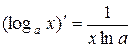 .
. . 14.
. 14.  .
.
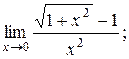
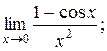


 в)
в) 
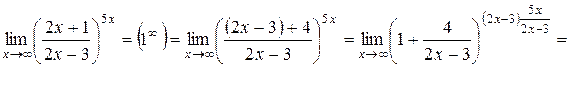
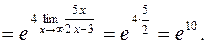
 на непрерывность в точках
на непрерывность в точках  ,
,  .
.
 .
. .
. .
. .
. .
.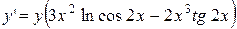 .
. .
. .
. , считая
, считая  функцией от
функцией от  .
. .
. . 16.
. 16.  .
.









 12.
12. 
 14.
14. 
 16.
16. 
 18.
18. 
 20.
20. 
 22.
22. 
 24.
24. 
 26.
26. 
 28.
28. 
 30.
30. 
 (координаты – декартовы прямоугольные) и О (0,0,0) – начало координат. Найти: 1) угол между ребрами АB и AC; 2) уравнение плоскости ABC; 3) площадь треугольника АВС; 4) векторное произведение векторов
(координаты – декартовы прямоугольные) и О (0,0,0) – начало координат. Найти: 1) угол между ребрами АB и AC; 2) уравнение плоскости ABC; 3) площадь треугольника АВС; 4) векторное произведение векторов  ; 5) объем пирамиды ABCO; 6) уравнение высоты опущенной из вершины О на грань ABC, если:
; 5) объем пирамиды ABCO; 6) уравнение высоты опущенной из вершины О на грань ABC, если:














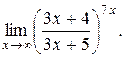

















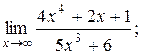











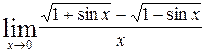

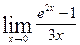
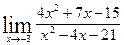















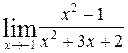

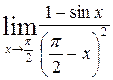

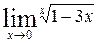










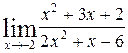

 данных функций.
данных функций.