Приложение № 1. Пример выполнения индивидуального задания
Вариант № 0
1. По данным неколлинеарным векторам  и и  построить векторы: построить векторы:   ; ;   ; ;   ; ;
  . .
2. Дано:  , ,  , ,  , ,  . .
Найти:  . .
3. Дано:  , ,  , ,  . .
Найти:
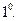  ; ;
  ; ;
  ; ;
 Площадь параллелограмма, построенного на векторах Площадь параллелограмма, построенного на векторах 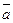 и и 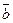 . .
 Площадь треугольника, построенного на векторах Площадь треугольника, построенного на векторах  , ,  . .
4. Даны векторы:  , ,  . .
Найти:
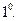 Координаты и модуль вектора Координаты и модуль вектора  ; ;
 Направляющие косинусы вектора Направляющие косинусы вектора  ; ;
   ; ;
  ; ;
 Угол между векторами Угол между векторами  и и  ; ;
60. Площадь треугольника, построенного на векторах  и и  ; ;
5. Даны вершины треугольника:  , ,  , ,  . .
Сделать схематический рисунок и найти:
  ; ;
 Разложение по ортам вектора Разложение по ортам вектора 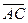 ; ;
 Направляющие косинусы вектора Направляющие косинусы вектора  ; ;
 Периметр треугольника Периметр треугольника  ; ;
 Медиану Медиану  ; ;
 Угол при вершине Угол при вершине 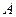 . .
70. Площадь треугольника 
 Высоту Высоту  . .
6. Сила  приложена к точке приложена к точке  Найти момент этой силы относительно начала координат. Найти момент этой силы относительно начала координат.
6*. Вычислить работу, которую производит сила  , если точка ее приложения перемещается из начала в конец вектора , если точка ее приложения перемещается из начала в конец вектора  , причем , причем  
Решение задачи индивидуального задания
 1. По данным неколлинеарным векторам 1. По данным неколлинеарным векторам  и и  построить векторы: построить векторы:   ; ;   ; ;   ; ;
  . .
Даны два вектора:
Решение.
 10. 10.  20. 20. 
30. 
40. 
2. Дано:  , ,  , , 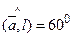 , ,  . .
Найти  . .
Решение.Воспользуемся свойствами аддитивности и однородности проекций и выражением проекции чрез ее модуль и угол между вектором и осью.
 


3. Дано:  , ,  , ,  . .
Найти:
10. Скалярное произведение:  . .
Решение. В соответствии с определением понятия скалярного произведения двух векторов получаем:

Ответ. 
20. Скалярное произведение двучленов:
 . .
Решение. Выполним действия по правилам преобразования алгебраических многочленов:



Ответ. 
30. Модуль разности векторов:  . .
Решение. Воспользуемся формулой вычисления модуля вектора  : :



Ответ. 
40. Площадь параллелограмма, построенного на векторах 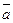 и и 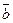 . .
Решение. Площадь параллелограмма определяется формулой:

Ответ. 
 Площадь треугольника, построенного на векторах Площадь треугольника, построенного на векторах  , ,  . .
Решение. Площадь треугольника, построенного на векторах  и и  , равна половине модуля векторного произведения данных векторов. Вычислим векторное произведение векторов , равна половине модуля векторного произведения данных векторов. Вычислим векторное произведение векторов  и и  по правилу преобразования многочленов с учетом свойства «антикоммутативности»: по правилу преобразования многочленов с учетом свойства «антикоммутативности»:
 


Ответ. 
4. Даны векторы:  , ,  . .
Найти:
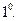 Координаты и модуль вектора Координаты и модуль вектора  . .
Решение. Введем обозначение:   , и вычислим координаты вектора , и вычислим координаты вектора 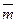 и его модуль: и его модуль:
 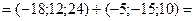

Модуль вектора 


Ответ: искомые координаты:

искомый модуль: 
 Направляющие косинусы вектора Направляющие косинусы вектора  . .
Решение.Введем обозначение:   и вычислим координаты и модуль вектора и вычислим координаты и модуль вектора  : :





Вычислим направляющие косинусы вектора
  : :



Найдем сумму квадратов направляющих косинусов:


Ответ. Направляющие косинусы вектора  равны: равны:



 Скалярное произведение двучленов: Скалярное произведение двучленов:

Решение.Здесь можно пойти двумя путями:
· перемножить двучлены, а затем представить векторы в координатной форме и выполнить действия;
· сразу же представить векторы в координатной форме, и далее все действия осуществлять в этой форме.
Второй путь, с нашей точки зрения, более рационален.

 = =



=20–40+32=12.
Ответ. 
 Проекцию вектора Проекцию вектора  на вектор на вектор  
Решение. 

Ответ. 
 Угол между векторами Угол между векторами  и и  . .
Решение.Найдем косинус угла между данными векторами  и и  : :



Ответ. 
60. Площадь треугольника, построенного на векторах  и и  . .
Решение. Площадь треугольника, построенного на векторах, равна половине модуля векторного произведения этих векторов. Вычислим это произведение:



Найдем модуль векторного произведения:

Отсюда

Ответ. 
5. Даны вершины треугольника:  , ,  , ,  (рис. 7.1). (рис. 7.1).
Найти:
 Длину стороны Длину стороны 
 Решение. Для определения длины стороны Решение. Для определения длины стороны  рассмотрим вектор рассмотрим вектор  , найдем координаты и модуль этого вектора: , найдем координаты и модуль этого вектора:




Ответ. 
 Разложение по ортам вектора Разложение по ортам вектора 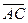 . .
Решение. Определим координаты вектора 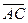 , а затем его разложение по ортам: , а затем его разложение по ортам:
 
Ответ. 
 Направляющие косинусы вектора Направляющие косинусы вектора  . .
Решение. Найдем координаты и модуль вектора  : :


Вычислим направляющие косинусы вектора  : :



Найдем сумму квадратов направляющих косинусов:


Ответ. Направляющие косинусы вектора  равны: равны:



 Периметр треугольника Периметр треугольника 
Решение. Длины сторон  и и  известны, известны,  , ,  Длину стороны Длину стороны  вычислим по известным координатам вектора вычислим по известным координатам вектора 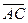 : :

Периметр треугольника равен:
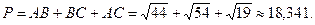
Ответ. 
 Медиану Медиану  . .
Решение. Определим координаты точки  Поскольку точка Поскольку точка  является серединой отрезка является серединой отрезка  , то ее координаты вычислим по формулам: , то ее координаты вычислим по формулам:



Точки  имеет координаты: имеет координаты:  . .
Вычислим координаты вектора  : :

и наконец, найдем медиану 

Ответ. Медиана 
60. Угол при вершине 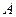 . .
Решение. Угол  определим как угол между векторами определим как угол между векторами  и и 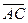 . .



Ответ. Угол между векторами  и и  равен: равен:

70. Площадь треугольника 
Решение. Площадь  равна половине модуля векторного произведения каких-либо векторов, образующих этот треугольник, например, векторов равна половине модуля векторного произведения каких-либо векторов, образующих этот треугольник, например, векторов  и и 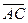 (рис 7.1). (рис 7.1).
Вычислим векторное произведение этих векторов, используя формулу (6.7):
 
Координаты векторов  и и  нам известны: нам известны:
 
Вычислим их векторное произведение:

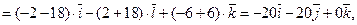
 
Найдем площадь треугольника:
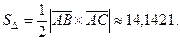
Ответ. 
80. Высоту 
Решение. Площадь  равна половине произведения основания на высоту. В данном треугольнике AC –основание, BE –высота(рис. 7.1). Следовательно, равна половине произведения основания на высоту. В данном треугольнике AC –основание, BE –высота(рис. 7.1). Следовательно,

Отсюда получаем:

Ответ. 
6. Сила  приложена к точке приложена к точке  Найти момент этой силы относительно начала координат. Найти момент этой силы относительно начала координат.
Решение. Моментом силы  относительно начала координат является вектор, равный векторному произведению радиус-вектора относительно начала координат является вектор, равный векторному произведению радиус-вектора  точки точки  на вектор силы на вектор силы  Координаты радиус-вектора Координаты радиус-вектора  совпадают с координатами точки совпадают с координатами точки  , поэтому , поэтому  Отсюда следует: Отсюда следует:



Ответ.  
6*. Вычислить работу, которую производит сила  , если точка ее приложения перемещается из начала в конец вектора , если точка ее приложения перемещается из начала в конец вектора  , причем , причем  
Решение. Работа  силы силы  на перемещении на перемещении  равна скалярному произведению векторов равна скалярному произведению векторов  и и  Найдем координаты вектора Найдем координаты вектора 



Ответ. 
Приложение № 2
Индивидуальные задания
Вариант № 1
1. По данным неколлинеарным векторам  и и  построить векторы: построить векторы:   ; ;   ; ;   ; ;
  . .
2. Дано:  , ,  , ,  , ,  . .
Найти:  . .
3. Дано:  , , 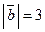 , ,  . .
Найти:
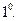  ; ;
  ; ;
  ; ;
 Площадь параллелограмма, построенного на векторах Площадь параллелограмма, построенного на векторах 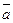 и и 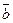 ; ;
 Площадь треугольника, построенного на векторах Площадь треугольника, построенного на векторах  , ,  . .
4. Даны векторы:  , ,  . .
Найти:
 Координаты и модуль вектора Координаты и модуль вектора  ; ;
 Направляющие косинусы вектора Направляющие косинусы вектора  ; ;
   ; ;
  ; ;
 Угол между векторами Угол между векторами  и и  ; ;
 Площадь треугольника, построенного на векторах Площадь треугольника, построенного на векторах  и и  . .
5. Даны вершины треугольника:  , ,  , ,  . .
Сделать схематический рисунок и найти:
  ; ;
 Разложение по ортам вектора Разложение по ортам вектора 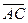 ; ;
 Направляющие косинусы вектора Направляющие косинусы вектора  ; ;
 Периметр треугольника Периметр треугольника  ; ;
 Медиану Медиану  ; ;
 Угол при вершине Угол при вершине  . .
 Площадь треугольника Площадь треугольника  ; ;
 Высоту Высоту  . .
6. Сила  приложена к точке приложена к точке 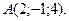 Найти момент этой силы относительно начала координат. Найти момент этой силы относительно начала координат.
Вариант № 2
1. По данным неколлинеарным векторам 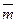 и и  построить векторы: построить векторы:   ; ;   ; ;   ; ;
  . .
2. Дано:  , , 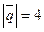 , ,  , , 
Найти:  . .
3. Дано:  , ,  , , 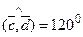 . .
Найти:
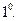  ; ;
  ; ;
  ; ;
 Площадь параллелограмма, построенного на векторах Площадь параллелограмма, построенного на векторах  и и  ; ;
 Площадь треугольника, построенного на векторах Площадь треугольника, построенного на векторах  , ,  . .
4. Даны векторы:  , ,  . .
Найти:
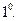 Координаты и модуль вектора Координаты и модуль вектора  ; ;
 Направляющие косинусы вектора Направляющие косинусы вектора  ; ;
 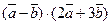 ; ;
  ; ;
 Угол между векторами Угол между векторами 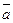 и и  ; ;
 Площадь треугольника, построенного на векторах Площадь треугольника, построенного на векторах 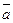 и и  . .
5. Даны вершины треугольника:  , ,  , ,  . .
Сделать схематический рисунок и найти:
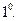  ; ;
 Разложение по ортам вектора Разложение по ортам вектора  ; ;
 Направляющие косинусы вектора Направляющие косинусы вектора  ; ;
 Периметр треугольника Периметр треугольника  ; ;
 Медиану Медиану  ; ;
 Угол при вершине Угол при вершине  . .
 Площадь треугольника Площадь треугольника  ; ;
 Высоту Высоту  . .
6. Вычислить работу, которую производит сила  , если точка ее приложения перемещается из начала в конец вектора , если точка ее приложения перемещается из начала в конец вектора  , причем , причем  
Вариант № 3
1. По данным неколлинеарным векторам  и и  построить векторы: построить векторы:   ; ;   ; ;   ; ;
  . .
2. Дано:  , ,  , ,  , ,  . .
Найти  . .
3. Дано:  , ,  , ,  . .
Найти:
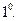  ; ;
  ; ;
  ; ;
 Площадь параллелограмма, построенного на векторах Площадь параллелограмма, построенного на векторах 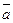 и и 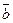 ; ;
 Площадь треугольника, построенного на векторах Площадь треугольника, построенного на векторах  , ,  . .
4. Даны векторы:  , ,  . .
Найти:
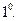 Координаты и модуль вектора Координаты и модуль вектора  ; ;
 Направляющие косинусы вектора Направляющие косинусы вектора  ; ;
  ; ;
  ; ;
 Угол между векторами Угол между векторами  и и  ; ;
 Площадь треугольника, построенного на векторах Площадь треугольника, построенного на векторах  и и  . .
5. Даны вершины треугольника:  , ,  , ,  . .
Найти:
  ; ;
 Разложение по ортам вектора Разложение по ортам вектора 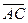 ; ;
 Направляющие косинусы вектора Направляющие косинусы вектора  ; ;
 Периметр треугольника Периметр треугольника  ; ;
 Медиану Медиану  ; ;
 Угол при вершине Угол при вершине  ; ;
 Площадь треугольника Площадь треугольника  ; ;
 Высоту Высоту  . .
6. Сила  приложена к точке приложена к точке  . Найти момент этой силы относительно начала координат. . Найти момент этой силы относительно начала координат.
Вариант № 4
1. По данным неколлинеарным векторам 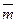 и и  построить векторы: построить векторы: 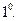  ; ;   ; ;   ; ;
  . .
2. Дано:  , ,  , ,  , , 
Найти:  . .
3. Дано:  , ,  , , 
Найти:
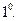  ; ;
  ; ;
  ; ;
 Площадь параллелограмма, построенного на векторах Площадь параллелограмма, построенного на векторах  и и  ; ;
 Площадь треугольника, построенного на векторах Площадь треугольника, построенного на векторах  ; ;  . .
4. Даны векторы:  , ,  . .
Сделать схематический рисунок и найти:
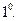 Координаты и модуль вектора Координаты и модуль вектора  ; ;
 Направляющие косинусы вектора Направляющие косинусы вектора  ; ;
  ; ;
  ; ;
 Угол между векторами Угол между векторами 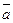 и и 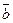 ; ;
 Площадь треугольника, построенного на векторах Площадь треугольника, построенного на векторах 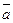 и и 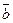 . .
5. Даны вершины треугольника:  , ,  , ,  . .
|
 и
и  построить векторы:
построить векторы: 
 ;
; 
 ;
; 
 ;
;
 .
. ,
,  ,
,  ,
,  .
. .
. ,
,  ,
,  .
.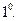
 ;
;
 ;
;
 ;
; Площадь параллелограмма, построенного на векторах
Площадь параллелограмма, построенного на векторах 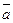 и
и 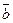 .
. Площадь треугольника, построенного на векторах
Площадь треугольника, построенного на векторах  ,
,  .
. ,
,  .
. ;
; ;
;
 ;
; ;
; и
и  ;
; ,
,  ,
,  .
.
 ;
;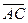 ;
; ;
; ;
; ;
; Угол при вершине
Угол при вершине 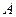 .
.
 Высоту
Высоту  .
. приложена к точке
приложена к точке  Найти момент этой силы относительно начала координат.
Найти момент этой силы относительно начала координат. , если точка ее приложения перемещается из начала в конец вектора
, если точка ее приложения перемещается из начала в конец вектора  , причем
, причем 

 1. По данным неколлинеарным векторам
1. По данным неколлинеарным векторам  ;
;  ;
;

 10.
10.  20.
20. 

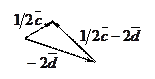

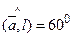 ,
,  .
.









 .
. :
:











 и его модуль:
и его модуль:
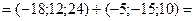







 :
:




 :
:









 =
=


















 (рис. 7.1).
(рис. 7.1).
 Решение. Для определения длины стороны
Решение. Для определения длины стороны 















 известны,
известны,  ,
,  Длину стороны
Длину стороны  вычислим по известным координатам вектора
вычислим по известным координатам вектора 
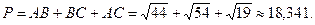

 Поскольку точка
Поскольку точка  является серединой отрезка
является серединой отрезка 


 .
. :
:


 определим как угол между векторами
определим как угол между векторами 



 равна половине модуля векторного произведения каких-либо векторов, образующих этот треугольник, например, векторов
равна половине модуля векторного произведения каких-либо векторов, образующих этот треугольник, например, векторов 




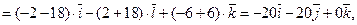


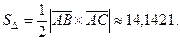





 приложена к точке
приложена к точке  относительно начала координат является вектор, равный векторному произведению радиус-вектора
относительно начала координат является вектор, равный векторному произведению радиус-вектора  точки
точки 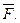 Координаты радиус-вектора
Координаты радиус-вектора  Отсюда следует:
Отсюда следует:




 силы
силы  Найдем координаты вектора
Найдем координаты вектора 




 ;
;  ;
; .
. ,
,  ,
,  ,
,  .
. ,
,  ,
,  .
. ;
; ;
; ,
,  .
. ,
,  .
. ,
,  ,
,  .
. Площадь треугольника
Площадь треугольника  приложена к точке
приложена к точке 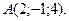 Найти момент этой силы относительно начала координат.
Найти момент этой силы относительно начала координат. ;
;  ;
;  ;
;  .
. ,
, 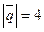 ,
,  ,
, 
 .
. ,
,  ,
, 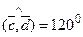 .
. ;
; ;
;
 ;
; ,
,  .
. ,
,  .
. ;
; ;
;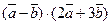 ;
; ;
; ;
; Площадь треугольника, построенного на векторах
Площадь треугольника, построенного на векторах  ,
,  ,
,  .
. ;
; ;
; ;
; ;
; ;
; .
. .
. , если точка ее приложения перемещается из начала в конец вектора
, если точка ее приложения перемещается из начала в конец вектора 

 ;
;  ;
;  ;
;  .
. ,
,  ,
,  ,
,  .
. .
. ,
,  ,
,  .
. ;
; ,
,  .
. ,
,  .
. ;
; ;
; ;
; ;
; ,
,  ,
,  .
. ;
; .
. приложена к точке
приложена к точке  . Найти момент этой силы относительно начала координат.
. Найти момент этой силы относительно начала координат. ;
;  ;
;  ;
;  .
. ,
,  ,
,  ,
, 
 .
. ,
,  ,
, 
 ;
; ;
; ;
; ;
;  .
. ,
,  .
. ;
; ;
; ;
; ;
; ,
,  ,
,  .
.