Анализ производства в долгосрочном периоде

В долгосрочном периоде не только труд, но и капитал, производственные технологии является переменным фактором производства. Технический прогресс означает, что тот же объем выпуска можно получить с меньшими затратами труда и капитала. Геометрически все изокванты сдвигаются вниз к началу координат (рис. 1.18):

Рис. 1.18. Сдвиг изокванты вследствие технического прогресса

В долгосрочном периоде не действует закон убывающей производительности какого-либо производственного фактора, т.к. все факторы изменяются. Поэтому применительно к данному периоду говорят только об отдаче от масштаба.

Отдача от масштаба показывает, во сколько раз возрастает выпуск при увеличении всех факторов производства в n раз.

Аналитически отдачу от масштаба можно определить по производственной функции вида:

Q =AK^aL^b,

где

· Q – заданный объем выпуска;

· L– количество используемого труда;

· K – количество используемого капитала.

· А– заданный параметр отражающий влияние технического прогресса на производство. Если производитель внедряет передовые технологии, величина данного параметра возрастает, т.е. выпуск увеличивается при прежних количествах труда и капитала.

· aи b - это коэффициенты эластичности выпуска соответственно по капиталу и труду.

Отдача от масштаба бывает трех видов:

1) возрастающая отдача от масштаба - при увеличении всех факторов производства в n раз выпуск возрастает более чем в n раз;

2) убывающая отдача от масштаба- при увеличении всех факторов производства в n раз выпуск возрастает менее чем в n раз;

3) постоянная отдача от масштаба - при увеличении всех факторов производства в n развыпуск возрастает тоже в n раз.

Коэффициент эластичности выпуска от масштаба рассчитывается по формуле:

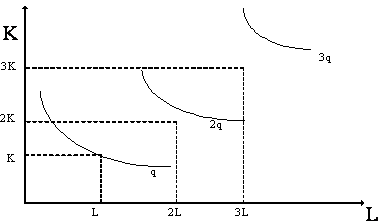
Геометрически все три случая будут выглядеть так. При постоянной отдаче от масштаба расстояние между изоквантами остается прежним (рис. 1.19).

Рис. 1.19. Постоянная отдача от масштаба

При возрастающей отдаче от масштаба расстояние между изоквантами все время сокращается (рис. 1.20):

Рис. 1.20. Возрастающая отдача от масштаба.

При убывающей отдаче от масштаба расстояние между изоквантами увеличивается (рис. 1.21):

Рис. 1.21. Убывающая отдача от масштаба

На практике, когда предприятие начинает увеличивать труд и капитал, оно сначала сталкивается с возрастающей отдачей от масштаба. Например, при росте труда и капитала в два раза, выпуск увеличивается втрое, что говорит о сокращении затрат на единицу продукции и о повышении эффективности производства. Однако дальнейшее увеличение используемых ресурсов рано или поздно приводит к тому, что возрастающая отдача от масштаба сменяется постоянной, а затем и убывающей. Эффективность производства падает. Это служит сигналом к тому, что предприятие стало слишком крупным и его размер целесообразно уменьшить.

Теорема ДжонсонаВикселля:

В долгосрочном периоде (Q =AK^aL^b), эластичность выпуска от масштаба равна сумме эластичностей выпуска от используемых факторов производства:

εQm =εQ_L+εQ_K,

где

a =εQ_L

b =εQ_K.

Отсюда:

· при a+b=1 выпуск возрастает ровно в n раз, т.е. отдача от масштаба постоянна.

· при a+b>1 выпуск увеличивается более чем в n раз, т.е. отдача от масштаба возрастает.

· при a+b<1 выпуск увеличивается менее чем в n раз, т.е. имеет место убывающая отдача от масштаба.

Равновесие производителя.

Изокоста – это линия, точки на которой отражают всевозможные варианты каждой пары ресурсов K и L, которые может приобрести производитель при данных их ценах и номинальном доходе.

Рис. 1.22. Изокоста.

Уравнение изокосты:

Р_L×Q_L + Р_K×Q_K= ТС,

где

o Р_L и Р_K – цены факторов производства;

o Q_Lи QK– количество факторов производства;

o ТС – расходы (доход) производителя (величина постоянная).

Угол наклона изокосты к оси L определяется обратным соотношением цен на ресурсы.

Проанализируем экономическую ситуацию. Пусть нам дана производственная функция Q = 7K^2/9L^7/9.Цены на ресурсысоответственно составляют 4 и 3 условные единицы (у.е). Величина расходов производителя постоянная и равна 24 у. е.

Определим:

1. период производства;

2. количество ресурса, которое приобретет рациональный производитель при данных ценах и денежном доходе, исходя из сложившейся производственной задачи.

Рассуждения:

Анализируемый период производства долгосрочный, т.к. заданная производственная функция степенная.

Для того, чтобы определить количество ресурса, которое приобретет рациональный производитель воспользуемся правилами минимизации затрат или максимизации прибыли (рис. 1.23):

o производитель минимизирует затраты при условии, когда каждый последний рубль, затраченный им на ресурсы даёт одинаковый предельный продукт (правило минимизации затрат).

o предельные продукты всех факторов производства в стоимостном выражении равны их ценам, или каждый ресурс используется до тех пор, пока его предельный продукт в денежном выражении не станет равен цене (правило максимизации прибыли):

Рис. 1.23. Предельная производительность, цена и степень использования ресурса в производстве.

Первая производная производственной функцииQ = 7K^2/9L^7/9 даст нам следующие предельные величины:

MP_L =(Q)′L = ⁴⁹/₉(^K/ _L)^2/9

MP_K = (Q)′K = ¹⁴/₉ (^L/_K)^7/9

Если мы соответствующие предельные величины соотнесем с их ценами, то получим тождество:

22(^K/ _L)^2/9 = 5(^L/_K)^7/9

Согласно данным правилам производитель должен израсходовать весь свой денежный ресурс, поэтому составим следующую систему уравнений и решим ее:

Мы получим, что рациональный производитель приобретет количество единиц труда L = 6,3,капиталаK = 1,3.

Геометрически равновесие производителя можно отобразить следующим образом (рис. 1.24):

Рис. 1.24. Равновесие производителя.