|
|
Учебно-методические материалы по разделам курса физики3.1 Физические основы классической механики 3.1.1 Основные формулы. Кинематическое уравнение движения материальной точки (центра масс твердого тела) вдоль оси x x = f(t), где x = f(t) – некоторая функция времени. Проекция средней скорости на ось x
Средняя путевая скорость
где Δs – путь, пройденный точкой за интервал времени Δt. Путь Δs в отличие от разности координат Δx = x2 – x1 не может убывать и принимать отрицательные значения, т. е. Δs
Проекция среднего ускорения на ось x
Проекция мгновенного ускорения на ось x
Кинематическое уравнение движения материальной точки по окружности φ = f(t), r =R =const.
Модуль угловой скорости
Модуль углового ускорения
Связь между модулями линейных и угловых величин, характеризующих движение точки по окружности: V = ω R; aτ = ε R; an = ω2 R,
где V – модуль линейной скорости; aτ и an – модули тангенциального и нормального ускорений; ω – модуль угловой скорости; ε– модуль углового ускорения; R – радиус окружности. Модуль полного ускорения
Угол между полным
α = arccos(an / a).
Импульс материальной точки массой m, движущейся со скоростью
Второй закон Ньютона:
где Силы, рассматриваемые в механике: – сила упругости
где k – коэффициент упругости (в случае пружины-жесткость); D – сила гравитационного взаимодействия F = γ
где γ – гравитационная постоянная; m1 и m2 – массы взаимодействующих тел; r – расстояние между телами (тела рассматриваются как материальные точки); – сила тяжести
где g – ускорение свободного падения. В случае гравитационного притяжения тела массой к Земле
где М и R – масса и радиус Земли соответственно; – сила трения (скольжения)
F = μN,
где μ – коэффициент трения; N – сила нормального давления. Закон сохранения импульса:
или для двух тел (i = 2)
где
Кинетическая энергия тела, движущегося поступательно,
T = mV2 / 2,
или
T = p2 / 2m.
Потенциальная энергия: – упругодеформированной пружины П = k x2 / 2,
где k – жесткость пружины; x – абсолютная деформация; – гравитационного взаимодействия
где γ – гравитационная постоянная; m1 и m2 – массы взаимодействующих тел; r – расстояние между ними (тела рассматриваются как материальные точки); – тела, находящегося в однородном поле силы тяжести,
П = mgh,
где g – ускорение свободного падения; h – высота тела над уровнем, принятым за нулевой (формула справедлива при условии h << R, здесь R – радиус Земли). Закон сохранения механической энергии:
E = T + П = const.
Работа А, совершаемая результирующей силой, определяется как мера изменения кинетической энергии материальной точки:
А =
Основное уравнение динамики вращательного движения относительно неподвижной оси z
где
Jz – момент инерции относительно оси вращения. Моменты инерции некоторых тел массой m относительно оси z, проходящей через центр масс: – стержня длиной L относительно оси, перпендикулярной стержню,
– обруча (тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра),
Jz = m R2,
где R – радиус обруча (цилиндра); – диска радиусом R относительно оси, перпендикулярной плоскости диска,
Проекция на ось z момента импульса тел, вращающихся относительно неподвижной оси z,
Lz = Jω,
где ω – угловая скорость тела. Закон сохранения момента импульса систем тел, вращающихся вокруг неподвижной оси z,
Jz
где Jz – момент инерции системы тел относительно оси z;
Кинетическая энергия тела, вращающегося вокруг неподвижной оси z,
T =
или T = Lz2 / (2 Jz).
Релятивистское (лоренцево) сокращение длины стержня
где l0 – длина стержня в системе, относительно которой стержень покоится (собственная длина); l – длина стержня, относительно которой он движется; β – скорость частицы, выраженная в долях скорости света Промежуток времени ∆t в системе, движущейся по отношению к наблюдателю, связан с промежутком времени ∆t0 в неподвижной для наблюдателя системе отношением
Релятивистская масса
где m0 – масса покоя. Релятивистский импульс
Полная энергия релятивистской частицы
где Т – кинетическая энергия частицы;
Связь полной энергии с импульсом релятивистской частицы:
Связь кинетической энергии с импульсом релятивистской частицы:
3.1.2. Примеры решения задач. Пример 1Уравнение движения материальной точки вдоль оси имеет вид: x = A + Bt + Ct 3, где A = 2 м, B = 1 м/с, C = - 0,5 м/с3. Найти координату x, скорость Vx и ускорение ах точки в момент времени t = 2 с.
первая производная от координаты по времени: Vx = Ускорение точки найдем, взяв первую производную от скорости по времени: В момент времени t = 2 с
Vx = 1 – 3·0,5·2 2 = - 5 м/с; ах = 6(-0,5)·2 = - 6 м/с2.
Пример 2. Тело вращается вокруг неподвижной оси по закону
Так как
Модули
где Тогда (1) можно записать в виде
Угловую скорость ω найдем, взяв первую производную углаповорота по времени:
Угловое ускорение ε найдем, взяв первую производную от угловой скорости по времени:
Подставив в (2) значения ω,ε и r , получим
Пример 3.Тело массой m = 1кг движется вдоль оси х так, что его координата изменяется во времени по закону
Для нахождения силы, воспользуемся 2-м законом Ньютона:
Пример 4 Маховик в виде сплошного диска радиусом R = 0,2 м и массой m = 50 кг раскручен до частоты вращения n1 = 480 мин-1 и предоставлен сам себе. Под действием сил трения маховик остановился через t = 50 с. Найти момент М сил трения.
Z, совпадающей с геометрической осью маховика, за интервал времени dt; MZ − момент внешних сил (в данном случае момент сил трения), действующих на маховик относительно оси Z. Момент сил трения можно считать не изменяющимся с течением времени (МZ = const), поэтому интегрирование уравнения приводит к выражению
При вращении твердого тела относительно неподвижной оси изменение проекции момента импульса
где JZ − момент инерции маховика относительно оси Z;
Приравняв правые части двух предыдущих равенств, получим MZ
Момент инерции маховика в виде сплошного диска определяется по формуле JZ = 1/2mR2. Изменение угловой скорости
Подставив в формулу для MZ выражения JZ и MZ = πmR2(n2− n1) /
Проверим, дает ли расчетная формула единицу измерения момента силы. Для этого в правую часть формулы вместо символов величин подставим их единицы:
Подставляем численные значения и производим вычисления:
Знак минус показывает, что момент сил трения оказывает на маховик тормозящее действие. Пример 5. Шар массой m = 10 кг и радиусом R = 0,2 м вращается относительно оси, проходящей через его центр. Уравнение вращения имеет вид:
Для нахождения момента сил, действующих на шар, воспользуемся основным законом динамики вращательного движения:
В момент времени t = 2 с:
Пример 6.Две шайбы массами m1 = 2,5 кг и m2 = 1,5 кг движутся навстречу друг другу со скоростями V1 = 6 м/c и V2 = 2 м/c. Определить: 1) скорости шайб после удара; 2) кинетические энергии шайб до и после удара; 3) долю кинетической энергии шайб, превратившейся во внутреннюю энергию. Удар считать прямым, неупругим.
Определим эту скорость по закону сохранения импульса. Так как шайбы движутся по одной прямой, то этот закон можно записать в скалярной форме:
откуда
Направление скорости первой шайбы примем за положительное, тогда при вычислении скорость второй шайбы, которая движется навстречу первой, следует взять со знаком минус V2 = -2 м/с. Получим:
2) Кинетические энергии шайб до и после удара определим по формулам
Произведя вычисления по этим формулам, получим:
Т1 = 48 Дж; Т2 = 18 Дж.
3) Сравнение кинетических энергий шайб до и после удара показывают, что в результате неупругого удара произошло уменьшение их кинетической энергии за счет чего увеличилась их внутренняя энергия. Долю кинетической энергии шайб, пошедшей на увеличение их внутренней энергии, определим из соотношения:
Пример 7. Шайба массой m1, движущаяся горизонтально с некоторой скоростью V1, столкнулась с неподвижной массой m2. Шайбы абсолютно упругие, удар прямой. Какую долю w своей кинетической энергии первая шайба передала второй?
где: Т1 – кинетическая энергия первой шайбы до удара; U2 и Т21 – скорость и кинетическая энергия второй шайбы после удара. Для нахождения U2 воспользуемся тем, что при ударе абсолютно упругих тел одновременно выполняются два закона сохранения: импульса и механической энергии. По закону сохранения импульса, учитывая, что вторая шайба до удара покоилась, имеем:
По закону сохранения энергии
Решая совместно два последних уравнения, найдем:
Тогда:
Пример 8. Маховик в виде диска массой m = 50 кг и радиусом r = 20 см был раскручен до частоты вращения n = 480мин-1 и затем предоставлен самому себе. Вследствие трения маховик остановился. Найти момент М сил трения, считая его постоянным для двух случаев: 1) маховик остановился через t = 50 c; 2) маховик до полной остановки сделал N = 200 оборотов.
где:
Так как ώ2 = 0 и Δt = t, то Выразив угловую скорость через частоту вращения n1, (ω1 = 2πn1), получим:
2. В условии задачи дано число оборотов, сделанных маховиком до остановки, т.е. его угловое перемещение. Поэтому применим формулу, выражающую связь работы с изменением кинетической энергии:
Работа при вращательном движении Тогда имеем:
Знак минус показывает, что момент сил трения оказывает тормозящее действие.
Пример 9.Платформа в виде диска радиусом R = 1,5 м и массой m1 = 80 кг вращается по инерции около вертикальной оси с частотой n1 = 10 1мин = 1/6 с-1. В центре платформы стоит человек массой 60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?
Учитывая, что
откуда:
Пример 10. Определить релятивистский импульс Р и кинетическую энергию Т электрона движущегося со скоростью V = 0,9 c (где с = 3·108м/с – скорость света в вакууме) Во сколько раз релятивистская масса больше массы электрона?
В релятивистской механике кинетическая энергия Т частицы определяется как разность между полной энергией и энергией покоя Е0. Так как
Вычисляем Т:
Во внесистемных единицах измерения энергия покоя электрона Тогда:
Релятивистская масса больше массы покоя:
|
|
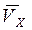 =
=

 0. Тогда проекция мгновенной скорости на ось x равна:
0. Тогда проекция мгновенной скорости на ось x равна:
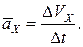



 .
.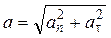 , или
, или 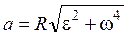 .
. и нормальным
и нормальным  ускорениями
ускорениями ,
,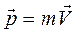 .
.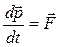 ,
, – результирующая сила, действующая на материальную точку.
– результирующая сила, действующая на материальную точку.
 ,
, – абсолютная деформация;
– абсолютная деформация;
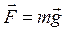 ,
,

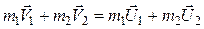 ,
, и
и  – скорости тел в момент времени, принятый за начальный;
– скорости тел в момент времени, принятый за начальный;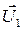 и
и  – скорости тех же тел в конечный момент времени.
– скорости тех же тел в конечный момент времени. ,
, T = T2 – T1.
T = T2 – T1. ,
,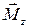 – результирующий момент внешних сил относительно оси z, действующих на тело;
– результирующий момент внешних сил относительно оси z, действующих на тело; – угловое ускорение;
– угловое ускорение; ;
;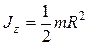 .
.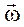 = const,
= const, – угловая скорость вращения тел системы вокруг оси z.
– угловая скорость вращения тел системы вокруг оси z. ,
,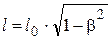 ,
, .
. .
. ,
,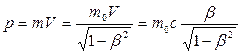 .
. ,
, – её энергия покоя,
– её энергия покоя,  .
. .
. .
. = В + 3Сt3.
= В + 3Сt3. .
. , где В = 20 рад/с; С = 2 рад/с2. Найти полное ускорение точки, находящейся на расстоянии r = 0,1м от оси вращения, для момента времени t = 4с.
, где В = 20 рад/с; С = 2 рад/с2. Найти полное ускорение точки, находящейся на расстоянии r = 0,1м от оси вращения, для момента времени t = 4с. точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения
точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения  āτ, направленного по касательной к траектории, и нормального ускорения ān, направленного к центру кривизны траектории.
āτ, направленного по касательной к траектории, и нормального ускорения ān, направленного к центру кривизны траектории.

 .
. , то модуль полного ускорения
, то модуль полного ускорения (1)
(1)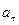 и
и 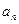 выражаются формулами
выражаются формулами ;
;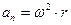 ,
, - модуль угловой скорости;
- модуль угловой скорости;  - модуль углового ускорения.
- модуль углового ускорения. =
=  . (2)
. (2) .
.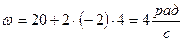 .
. .
. м/с2 = 1,65м/с2
м/с2 = 1,65м/с2 , где С = 1м/c2. Определить ускорение тела и действующую на тело силу к концу 5-ой секунды.
, где С = 1м/c2. Определить ускорение тела и действующую на тело силу к концу 5-ой секунды.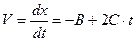 - зависимость скорости от времени.
- зависимость скорости от времени.

 LZ = MZ
LZ = MZ 
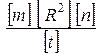 =
= 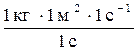 = 1 кг·м·с-2·1 м = 1 Н·м.
= 1 кг·м·с-2·1 м = 1 Н·м. = -1 Н·м.
= -1 Н·м. , где В = 4рад/c2, C = +1рад/c3. Найти закон изменения момента сил, действующих на шар. Определить момент сил М в момент времени t = 2с.
, где В = 4рад/c2, C = +1рад/c3. Найти закон изменения момента сил, действующих на шар. Определить момент сил М в момент времени t = 2с. .
Взяв производную от угловой скорости по времени,
получим закон изменения углового ускорения от времени :
.
Взяв производную от угловой скорости по времени,
получим закон изменения углового ускорения от времени :
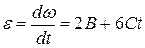
 , где
, где  - момент инерции шара относительно оси вращения, проходящей через центр масс шара. Таким образом:
- момент инерции шара относительно оси вращения, проходящей через центр масс шара. Таким образом: - закон изменения момента сил.
- закон изменения момента сил.
 ,
, .
. .
. ;
; 
 .
.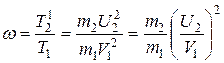 ,
, ;
; .
. ,
, .
.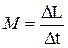
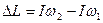 - изменение момента импульса;
- изменение момента импульса;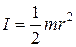
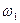 и
и  - начальная и конечная угловые скорости.
- начальная и конечная угловые скорости.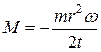 .
. .
.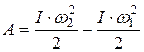 , или учитывая, что
, или учитывая, что 
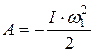 .
. .
. , учитывая, что
, учитывая, что  ,
,  ,
,  ,
,
 где:
где: 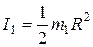 - момент инерции платформы;
- момент инерции платформы;
 - момент инерции человека, стоящего
в центре платформы (рассчитываем как для материальной точки);
- момент инерции человека, стоящего
в центре платформы (рассчитываем как для материальной точки);
 - момент инерции человека, стоящего на краю платформы.
- момент инерции человека, стоящего на краю платформы. - угловая скорость до перехода человека;
- угловая скорость до перехода человека; , будем иметь:
, будем иметь: ;
;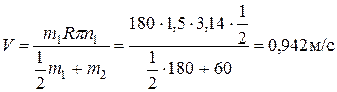
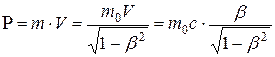 ,
где
,
где 
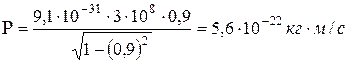 .
. , то учитывая зависимость массы от скорости, получим:
, то учитывая зависимость массы от скорости, получим: .
.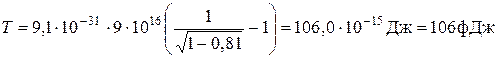 .
.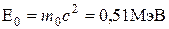
 .
.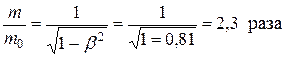 .
.