|
|
определенный интеграл и его основные свойстваГлава 5 Замена переменной интегрирования в неопределенном интеграле Теорема.Пусть функция
Формула называется формулой замены переменной в неопределённом интеграле. Метод замены переменной обычно применяется, когда подынтегральное выражение представляет собой независимую переменную, умноженную на многочлен от этой переменной, или на тригонометрическую функцию от этой переменной или на степенную функцию (в том числе корень) от этой переменной. Пример 1. Найти неопределённый интеграл методом замены переменной:
Решение. Положим x – 1 = t ; тогда x = t + 1. Отсюда dx = dt . По формуле (1)
Возвращаясь к переменной x, окончательно получаем
Интегрирование по частям в неопределенном интеграле Метод интегрирования по частям основан на использовании формулы дифференцирования произведения двух функций. Теорема.Пусть функции u(x)иv(x) определены и дифференцируемы на некотором промежутке Хи пусть функция
имеет первообразную на этом промежутке. Тогда на промежутке Х функция
также имеет первообразную и справедлива формула
Формула называется формулой интегрирования по частям в неопределённом интеграле. Так как
то её можно записать в виде
Пример 1.Найти неопределённый интеграл методом интегрирования по частям:
находим
определенный интеграл и его основные свойства Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где Пусть на отрезке [a,b] задана функция y = f(x). Разобьём отрезок [a,b] произвольным образом на n частей точками [x0 , x1], [x1 , x2], …, [xi-1 , xi], …, [xn-1 , xn]; длину i-го отрезка обозначим Свойства определённого интеграла: Теорема 1.Определённый интеграл с одинаковыми пределами интегрирования равен нулю, т.е.
Это свойство содержится в самом определении определённого интеграла. Однако его можно получить и по формуле Ньютона-Лейбница: Теорема 2.Величина определённого интеграла не зависит от обозначения переменной интегрирования, т.е.
Пусть F(x) – первообразная для f(x). Для f(t) первообразной служит та же функция F(t), в которой лишь иначе обозначена независимая переменная. Следовательно,
На основании формулы (39) последнее равенство означает равенство интегралов
и
Теорема 3.Постоянный множитель можно выносить за знак определённого интеграла, т.е.
Теорема 4.Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций, т.е.
Теорема 5.Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям, т.е. если
то
Теорема 6.При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак, т.е.
Теорема 7(теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке
Теорема 8.Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если
Теорема 9.Если верхний предел интегрирования больше нижнего и функции
можно почленно интегрировать, т.е.
|
|
 определена и дифференцируема на некотором промежутке Т и пусть Х – множество значений этой функции, на котором определена функция f(x). Тогда, если на множестве Х функция f(x) имеет первообразную, то на множестве Т справедлива формула
определена и дифференцируема на некотором промежутке Т и пусть Х – множество значений этой функции, на котором определена функция f(x). Тогда, если на множестве Х функция f(x) имеет первообразную, то на множестве Т справедлива формула





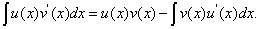
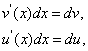




 ) называется приращение какой-нибудь её первообразной на этом отрезке.
) называется приращение какой-нибудь её первообразной на этом отрезке. :
:  ; максимальную из длин отрезков обозначим
; максимальную из длин отрезков обозначим 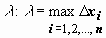 . На каждом из отрезков [xi-1 , xi] выберем произвольную точку
. На каждом из отрезков [xi-1 , xi] выберем произвольную точку  и составим сумму
и составим сумму  .
.  называется интегральной суммой. Если существует (конечный) предел последовательности интегральных сумм
называется интегральной суммой. Если существует (конечный) предел последовательности интегральных сумм  , не зависящий ни от способа разбиения отрезка [a,b] на части [xi-1 , xi], ни от выбора точек
, не зависящий ни от способа разбиения отрезка [a,b] на части [xi-1 , xi], ни от выбора точек  .
. 
 .
.  ; если b<a, то
; если b<a, то  .
.





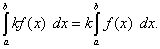




 внутри его, т.е.
внутри его, т.е.

 и
и  непрерывны, то неравенство
непрерывны, то неравенство
