|
|
Вихревые токи в электропроводящем полупространствеГЛАВА 2. Вихретоковые методы измерения толщины покрытий и изделий
Общая характеристика вихретоковых методов измерения толщины покрытий и изделий
Вихретоковый вид неразрушающего контроля применим для контроля изделий из электропроводящих ферро- и неферромагнитных материалов. Основан на анализе взаимодействия собственного электромагнитного поля вихретокового преобразователя с электромагнитным полем вихревых токов, наводимых в контролируемом объекте и зависящих от электрофизических и геометрических параметров основного металла и покрытия. В зависимости от задачи и свойств материала изделия и покрытия могут применяться различные функции изменения во времени электромагнитного поля (пробной энергии) и различные первичные информативные параметры, определяемые способом получения первичной информации. С использованием вихретоковых методов производят измерение толщины диэлектрических покрытий на электропроводящих ферро- и неферромагнитных основаниях, электропроводящих ферро- и неферромагнитных покрытий на электропроводящих ферро- и неферромагнитных основаниях, в разных сочетаниях, а также листовых электропроводящих материалов. Для описания сути вихретокового вида измерения и основных параметров, характеризующих его, рассмотрим явления взаимодействия вихретокового преобразователя с электропроводящим объектом на примере абсолютного трансформаторного двухобмоточного преобразователя без ферритовых (ферромагнитных) сердечника и экрана, возбуждаемого гармоническим напряжением. Функциональная модель абсолютного трансформаторного двухобмоточного первичного измерительного преобразователя без ферритовых сердечника и экрана, удаленного от электропроводящего объекта, приведена на рис 2.1.
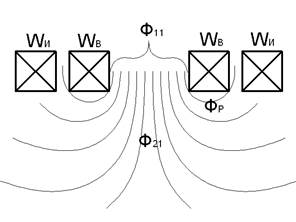
Рис. 2.1. Функциональная модель абсолютного трансформаторного двухобмоточного первичного измерительного преобразователя без ферритовых сердечника и экрана. Wв – обмотка возбуждения (первичная); Wи – измерительная (вторичная) обмотка
Магнитные потоки преобразователя Витки обмотки возбуждения Wв сцеплены с магнитным потоком самоиндукции Ф11, а витки измерительной обмотки Wи с магнитным потоком взаимной индукции Ф21. Магнитный поток Ф21, индуцирующий на вторичной обмотке ЭДС взаимоиндукции равен:
Ф21 = Ф11 – Фр, (2.1.1)
где Фр – магнитный поток рассеяния. Амплитуда магнитного потока самоиндукции Ф11 [Вб] определяется по формуле:
Ф11 = Lв Iв, (2.1.2)
где Lв – индуктивность обмотки возбуждения, [Гн]; Iв – амплитуда тока обмотки возбуждения, [А]. Индуктивность Lв обмотки возбуждения определяется ее геометрическими характеристиками:
Lв = m0 Wв2 Sв/ l, (2.1.3)
где m0 – магнитная постоянная; Wв – число витков обмотки возбуждения; Sв – площадь эквивалентного витка обмотки возбуждения [м2]; l – средняя длина магнитных линий контура, [м]. За счет существования магнитных потоков рассеяния Фр, магнитный поток взаимоиндукции Ф21 всегда меньше магнитного потока самоиндукции Ф11. Амплитуда магнитного потока взаимоиндукции Ф21 определяется следующим соотношением:
Ф21 = М12 Iв/ Wи, (2.1.4)
где Wи – число витков измерительной обмотки, М12 – коэффициент взаимной индукции между возбуждающей и измерительной обмотками [Гн]. Коэффициент взаимной индукции М12 определяется по формуле: _____ М12 = КÖ(LвLи), (2.1.5)
где Lв и Lи –индуктивности обмоток возбуждения и измерительной, соответственно; К – коэффициент связи, определяемый геометрией и взаимным расположением обмоток. Для рассматриваемого случая (отсутствуют ферритовые сердечник и экран) можно утверждать, что коэффициент связи обратно пропорционален потоку рассеяния. Таким образом, ЭДС взаимоиндукции e(t) будет равна:
e(t) = - Wи(dФ21(t)/dt) = - M12(diв(t)/dt) (2.1.6 )
Если ток обмотки возбуждения гармонический, iв (t) = Iмsin(wt), где w = 2pf – круговая частота, то ЭДС взаимоиндукции:
e(t) = - wWиФ21 cos(wt).
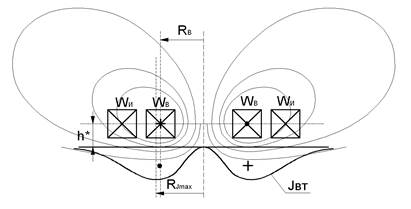
Вихревые токи в электропроводящем полупространстве Если в магнитное поле первичного измерительного преобразователя внести электропроводящий объект, то переменное электромагнитное поле индуцирует в объекте вихревые токи. По закону Ленца направление вихревого тока, а следовательно и магнитного потока, возбужденного им, в каждый момент времени будет направлено так, чтобы противодействовать магнитному потоку, породившему вихревой ток. Как следствие, картина магнитного поля первичного измерительного преобразователя с внесенным в его поле электропроводным объектом исказится. На рис. 2.2 изображена функциональная модель абсолютного трансформаторного двухобмоточного первичного измерительного преобразователя без ферритововых сердечника и экрана с внесенным в его поле электропроводящим объектом в виде полупространства, картина поля и распределение плотности вихревого тока Jвт, наведенного в образце. На рис. 2.2 изображено направление тока в обмотке возбуждения и направление вихревого тока в электропроводящем объекте контроля. Магнитное поле вихревых токов складывается с магнитным полем обмотки возбуждения по принципу суперпозиции.
Рис. 2.2. Функциональная модель абсолютного трансформаторного двухобмоточного первичного измерительного преобразователя без ферритовых сердечника и экрана с внесенным в его поле электропроводящим объектом в виде полупространства
Для расчета параметров взаимодействия первичного измерительного преобразователя с электропроводящим объектом контроля удобно отказаться от абсолютных величин и перейти к относительным, нормированным по радиусу обмотки возбуждения Rв. В этом случае относительный радиус обмотки возбуждения Rв*= Rв/ Rв = 1. Распределение плотности Jвт и значение фазы jвт вихревого тока в различных точках объема электропроводящего объекта под обмоткой возбуждения отлично. Наибольшая плотность вихревого тока наблюдается в случае, если зазор между обмоткой возбуждения и поверхностью контролируемого объекта h* = 0 (непосредственно возле поверхности объекта под эквивалентным витком обмотки возбуждения RJmax* = 1). В случае если существует зазор между обмоткой возбуждения и поверхностью объекта контроля h* > 0, то наибольшая плотность вихревых токов наблюдается на большем расстоянии от центра обмотки возбуждения (RJmax* > 1). Это обусловливается изменением формы магнитного поля обмотки возбуждения с увеличением зазора. Для ориентировочной оценки этой величины можно воспользоваться эмпирической формулой: RJmax = Rв + 1,5h* (2.1.7)
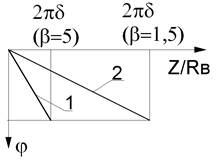
С увеличением глубины плотность вихревого тока уменьшается по закону, близкому к экспоненциальному. Значение фазы jвт вихревого тока в точке наибольшей плотности тока, непосредственно под поверхностью объекта контроля, сдвинуто на более чем на 1800 относительно тока в обмотке возбуждения. При удалении от поверхности вглубь, jвт увеличивается. Глубина проникновения вихревых токов определяется радиусом обмотки возбуждения, частотой тока возбуждения, электропроводностью и магнитной проницаемостью материала контролируемого объекта. Для расчета глубины проникновения вихревого тока и ЭДС, наводимой на измерительной обмотке, удобно использовать обобщенный параметр b, который учитывает влияние всех перечисленные выше параметров: _______ b = RÖ(wsm0mr), (2.1.8)
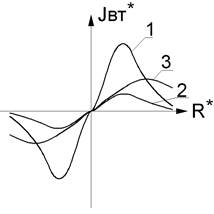
где R – эквивалентный радиус обмотки возбуждения, [м], (при h* = 0, R = Rв); w - круговая частота тока возбуждения, [рад/сек]; s – электропроводность основания, [См/м]; m0 – магнитная постоянная; mr – относительная магнитная проницаемость основания. На рис. 2.3 представлены графики распределения относительного значения плотности вихревого тока Jвт* = Jвт/(Iв R* Wв*) в зависимости от расстояния от оси преобразователя R* =R/Rв и глубины z* = z/ Rв.
а)
Рис.2.3. Зависимость относительного значения плотности вихревых токов: а - по поверхности: 1 – b = 5 (h* = 0); 2 – b = 1,5 (h* = 0); 3 – b = 5 (h* = 0,7), б - по глубине: 1 – b = 5 (h* = 0); 2 – b = 1,5 (h* = 0).
На рис. 2.4 изображены графики значения фазы вихревого тока по глубине z* и по расстоянию от оси преобразователя R*.
а)
Рис.2.4. Зависимость значения фазы вихревого тока: а - по поверхности; б - по глубине: 1 – b = 5 (h* = 0); 2 – b = 1,5 (h* = 0).
Для оценки относительной глубины проникновения вихревых токов d* = d/Rв можно использовать формулу определения глубины проникновения плоской волны с учетом поправочного коэффициента kф = 0,4+0,13 ln (b) kф _ d* =kф(Ö2 )/ b (2.1.9)
Разность фаз вихревого тока протекающего на глубине равной длине электромагнитной волны в металле l1=2pd и тока протекающего по поверхности составляет 2p. Глубину проникновения вихревых токов, равную 2pd считают максимальной глубиной проникновения вихревого тока.
|
|
 б)
б) 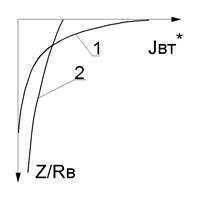
 б)
б)